Placa rectangular giratoria (CMR)
De Laplace
(Página creada con '==Enunciado== Sabiendo que el momento de inercia de una chapa rectangular de masa m, base b y altura h respecto a un eje tangente a la chapa, paralelo a la base por su centro es…') |
|||
| Línea 29: | Línea 29: | ||
<center><math>\bar{\bar{I}}=\begin{pmatrix}0.016 & 0 & 0 \\ 0 & 0.009 & 0 \\ 0 & 0 & 0.025\end{pmatrix}\,\mathrm{kg}\cdot \mathrm{m}^2</math></center> | <center><math>\bar{\bar{I}}=\begin{pmatrix}0.016 & 0 & 0 \\ 0 & 0.009 & 0 \\ 0 & 0 & 0.025\end{pmatrix}\,\mathrm{kg}\cdot \mathrm{m}^2</math></center> | ||
| + | ==Momento cinético== | ||
| + | Por tratarse de ejes principales, en el sistema 2 se cumple | ||
| + | <center><math>\vec{L}_O=I_{XX}\omega_X\vec{\imath}_2+I_{YY}\omega_Y\vec{\jmath}_2+I_{ZZ}\omega_Z\vec{k}_2</math></center> | ||
| - | == | + | Solo hay que pasar <math>\vec{\omega}_{21}</math> a esa base |
| + | |||
| + | <center><math>\vec{\omega}_{21}=100\vec{\jmath}_1=\omega_X\vec{\imath}_2+\omega_Y\vec{\jmath}_2</math></center> | ||
| + | |||
| + | Como | ||
| + | |||
| + | <center><math>\vec{\jmath}_1=\mathrm{sen}(\beta)\vec{\imath}_2+\cos(\beta)\vec{\jmath}_2=0.60\vec{\imath}_2+0.80\vec{\jmath}_2</math></center> | ||
| + | |||
| + | queda | ||
| + | |||
| + | <center><math>\vec{\omega}=60\vec{\imath}_2+80\vec{\jmath}_2\ (\mathrm{rad}/\mathrm{s})</math></center> | ||
| + | |||
| + | y | ||
| + | |||
| + | <center><math>\vec{L}_O=0.016\times 60\vec{\imath}_2+0.009\times 80\vec{\jmath}_2=0.96\vec{\imath}_2+0.72\vec{\jmath}_2\ (\mathrm{kg}\cdot\mathrm{m}^2/\mathrm{s})</math></center> | ||
==Energía cinética== | ==Energía cinética== | ||
==Par aplicado== | ==Par aplicado== | ||
==Fuerza sobre los rodamientos== | ==Fuerza sobre los rodamientos== | ||
Revisión de 00:19 14 feb 2019
Contenido |
1 Enunciado
Sabiendo que el momento de inercia de una chapa rectangular de masa m, base b y altura h respecto a un eje tangente a la chapa, paralelo a la base por su centro es IXX = mh2 / 12:
- Halle el tensor de inercia de una chapa de masa
, 
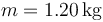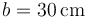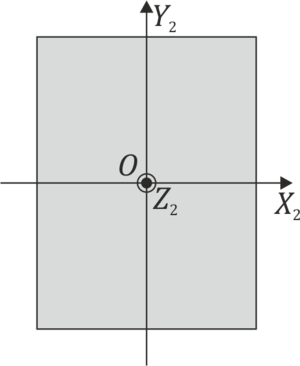
y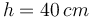 
respecto a un triedro ortogonal cuyos ejes pasan por el centro de la chapa y OX2 y OY2 son paralelos a los lados.
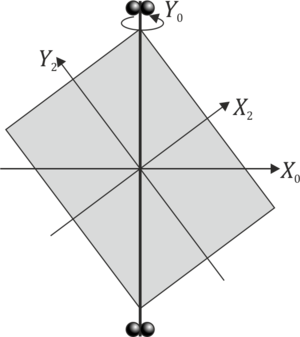
Suponga que esta chapa se monta sobre un eje fijo “1” que pasa por su diagonal y que está articulado mediante rodamientos sin fricción. Los rodamientos se hallan, cada uno de ellos, a una distancia de 60cm del centro de la chapa. Si la chapa se hace girar con velocidad angular constante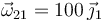 
(rad\/s), halle:
- El momento cinético respecto al centro de la chapa.
- La energía cinética de la chapa.
- El par aplicado respecto al CM para mantener el sistema en movimiento.
- La fuerza que la placa ejerce sobre los rodamientos en su rotación, suponiendo que estas fuerzas son puramente ortogonales al eje.
Puede despreciarse el efecto del peso. Puede emplearse un sistema intermedio “0” que gira con la misma velocidad angular pero que tiene su eje OY0 coincidente con el OY1
2 Tensor de inercia
Para el eje OX2
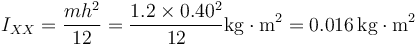
Para el eje OY2
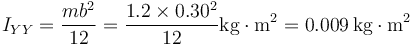
Para el eje OZ2, por ser una figura plana
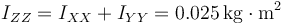
Los tres ejes son principales, por ser perpendiculares a planos de simetría, por lo que los productos de inercia son nulos. Por tanto
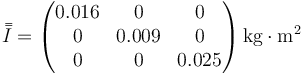
3 Momento cinético
Por tratarse de ejes principales, en el sistema 2 se cumple
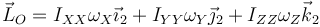
Solo hay que pasar 
a esa base
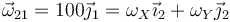
Como
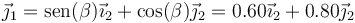
queda
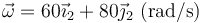
y
