Entrar Página Discusión Historial Go to the site toolbox

Partícula en montaña rusa (GIE)

De Laplace

(Diferencias entre revisiones)
(→Altura máxima)
(→Altura máxima)
 
(Una edición intermedia no se muestra.)
Línea 18: Línea 18:
La rapidez al cuadrado sale de la conservación de la energía mecánica
La rapidez al cuadrado sale de la conservación de la energía mecánica
-
<center><math>mgH = \frac{1}{2}m v^2_B + mgh \qquad\Rightarrow\qquad mV_B^2 = 2mg(H-h)</math></center>
+
<center><math>mgH = \frac{1}{2}m v^2_B + mgh \qquad\Rightarrow\qquad mv_B^2 = 2mg(H-h)</math></center>
Por tanto
Por tanto
Línea 24: Línea 24:
<center><math>mg = \frac{2mg(H-h)}{R}\qquad\Rightarrow\qquad H = h + \frac{R}{2}</math></center>
<center><math>mg = \frac{2mg(H-h)}{R}\qquad\Rightarrow\qquad H = h + \frac{R}{2}</math></center>
-
<center><math>h = 2\,\mathrm{m}</math></center> y R sale de aplicar el teorema de Pitágoras
+
<math>h = 2\,\mathrm{m}</math> y R sale de aplicar el teorema de Pitágoras
<center><math>(R-2)^2 + 4^2 = R^2 \qquad\Rightarrow \qquad R = 5\,\mathrm{m}</math></center>
<center><math>(R-2)^2 + 4^2 = R^2 \qquad\Rightarrow \qquad R = 5\,\mathrm{m}</math></center>

última version al 00:13 4 dic 2018

1 Enunciado

Una masa m de peso 10 N puede deslizar sin rozamiento por una pista al estilo de una montaña rusa formada por un plano inclinado de pendiente tg⁡(β) = 4/3, seguida de un valle en forma de arco de circunferencia que mide 8 m en línea recta (lo que se denomina “la cuerda”) y 2m de profundidad (lo que sería “la flecha”). Esta depresión es seguida por una cresta también en forma de arco de circunferencia de 8m de cuerda y 2m de flecha.

  1. Determine la altura máxima H desde la cual se puede soltar la masa si no se desea que salga volando al llegar a la cima de la cresta, B.
  2. Para la altura máxima anterior, calcule la reacción normal de la superficie cuando la masa pasa por el fondo del valle, A.

2 Altura máxima

En el punto B las fuerzas son perpendiculares a la trayectoria por lo que toda la aceleración es normal

F_n - mg = -m\frac{v_B^2}{R}

El valor máximo de H es el que hace Fn = 0

F_n=0\qquad\Rightarrow\qquad mg = m\frac{v_B^2}{R}

La rapidez al cuadrado sale de la conservación de la energía mecánica

mgH = \frac{1}{2}m v^2_B + mgh \qquad\Rightarrow\qquad mv_B^2 = 2mg(H-h)

Por tanto

mg = \frac{2mg(H-h)}{R}\qquad\Rightarrow\qquad H = h + \frac{R}{2}

h = 2\,\mathrm{m} y R sale de aplicar el teorema de Pitágoras

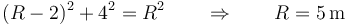
(R-2)^2 + 4^2 = R^2 \qquad\Rightarrow \qquad R = 5\,\mathrm{m}

Por tanto

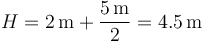
H = 2\,\mathrm{m}+\frac{5\,\mathrm{m}}{2}=4.5\,\mathrm{m}

3 Reacción en el punto más bajo

Ahora la reacción normal va hacia arriba

F_n - mg = \frac{mv_A^2}{R}\qquad\Rightarrow\qquad F_n = mg + \frac{mv_A^2}{R}

Por conservación de la energía, como antes,

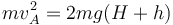
mv_A^2 = 2mg(H+h)\,

y por tanto

F_n = mg\left(1+\frac{2(H+h)}{R}\right)=10\,\mathrm{N}\left(1+\frac{2(4.5+2)}{5}\right)=36\,\mathrm{N}
Obtenido de "http://tesla.us.es/wiki/index.php/Part%C3%ADcula_en_monta%C3%B1a_rusa_(GIE)"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Esta página fue modificada por última vez el 00:13, 4 dic 2018. - Esta página ha sido visitada 1.470 veces. - Aviso legal - Acerca de Laplace