Test del primer parcial 2018-2019 (GIE)
De Laplace
(Página creada con '==Punto en un plano== Del punto <math>P(3,y,-2)</math> se sabe que está en el plano que es perpendicular al vector <math>\vec{B}=-2\vec{\jmath}+\vec{k}</math> y pasa por <math>…') |
(→Movimiento en polares) |
||
| (2 ediciones intermedias no se muestran.) | |||
| Línea 2: | Línea 2: | ||
Del punto <math>P(3,y,-2)</math> se sabe que está en el plano que es perpendicular al vector <math>\vec{B}=-2\vec{\jmath}+\vec{k}</math> y pasa por <math>A(2,-1,4).</math> ¿Cuánto vale la cantidad y? | Del punto <math>P(3,y,-2)</math> se sabe que está en el plano que es perpendicular al vector <math>\vec{B}=-2\vec{\jmath}+\vec{k}</math> y pasa por <math>A(2,-1,4).</math> ¿Cuánto vale la cantidad y? | ||
:* '''A''' −1. | :* '''A''' −1. | ||
| - | :* '''B''' − | + | :* '''B''' −2. |
| - | :* '''C''' − | + | :* '''C''' −4. |
:* '''D''' No hay información suficiente para determinarlo. | :* '''D''' No hay información suficiente para determinarlo. | ||
;Solución: | ;Solución: | ||
| Línea 48: | Línea 48: | ||
==Triedro de Frenet== | ==Triedro de Frenet== | ||
| - | (⊙: hacia afuera del papel; ⊗ hacia adentro del papel)? | + | ¿Cuál de las siguientes figuras representa correctamente la orientación de los vectores del triedro de Frenet (⊙: hacia afuera del papel; ⊗ hacia adentro del papel)? |
{| class="bordeado" | {| class="bordeado" | ||
| Línea 87: | Línea 87: | ||
La respuesta correcta es la '''<span style="color:red;">B<span>'''. | La respuesta correcta es la '''<span style="color:red;">B<span>'''. | ||
| - | [[Categoría: | + | [[Categoría:Preguntas de test de Física I (GIE)]] |
última version al 10:29 6 nov 2018
Contenido |
1 Punto en un plano
Del punto P(3,y, − 2) se sabe que está en el plano que es perpendicular al vector  y pasa por A(2, − 1,4). ¿Cuánto vale la cantidad y?
y pasa por A(2, − 1,4). ¿Cuánto vale la cantidad y?
- A −1.
- B −2.
- C −4.
- D No hay información suficiente para determinarlo.
- Solución
La respuesta correcta es la C.
2 Unidades de constantes
En un movimiento rectilíneo, en el que x es la posición, v la velocidad y t el tiempo se cumple
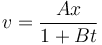
con A y B constantes. ¿En qué unidades se miden en el SI A y B?
- A A en s − 1, B es adimensional.
- B No hay información suficiente para saberlo.
- C ambas en s − 1.
- D No hay información suficiente para determinarlo.
- Solución
La respuesta correcta es la C.
3 Velocidad media en tramo
Un conductor recorre un túnel de longitud l, en el cual hay instalado un radar de tramo, estando la velocidad limitada a 75 km/h. A mitad de trayecto se da cuenta de que ha ido a 100 km/h. ¿A qué velocidad debe recorrer la otra mitad del trayecto para que su velocidad media sea 75 km/h?
- A Depende del valor de l.
- B A 50 km/h.
- C Es imposible conseguir esa velocidad media.
- D A 60 km/h.
- Solución
La respuesta correcta es la D.
4 Partícula en movimiento armónico simple
Una partícula sigue un movimiento armónico simple de frecuencia angular 2 rad/s. La posición inicial de la partícula es en  y su velocidad inicial es de
y su velocidad inicial es de 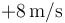 .
.
4.1 Pregunta 1
La posición de esta partícula como función del tiempo es en el SI
- A
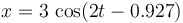 .
.
- B
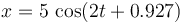 .
.
- C
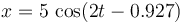 .
.
- D
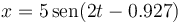 .
.
- A
- Solución
La respuesta correcta es la C.
4.2 Pregunta 2
¿Cuánto vale el fasor o amplitud compleja de la velocidad en este movimiento?
- A
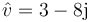 .
.
- B
 .
.
- C
 .
.
- D
 .
.
- A
- Solución
La respuesta correcta es la D.
5 Triedro de Frenet
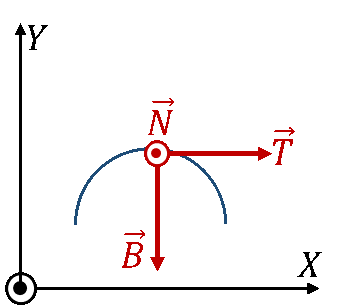
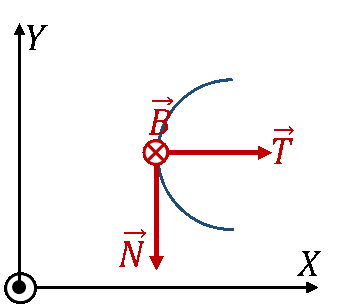
¿Cuál de las siguientes figuras representa correctamente la orientación de los vectores del triedro de Frenet (⊙: hacia afuera del papel; ⊗ hacia adentro del papel)?
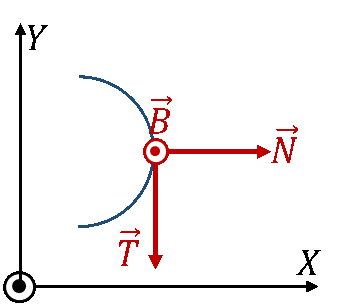
| 
|
| A | B |
| 
|
| C | D |
- Solución
La respuesta correcta es la D.
6 Movimiento circular
¿Cuál de las siguientes ecuaciones se cumple en un movimiento circular de radio R centrado en el origen de coordenadas?
- A
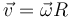 .
.
- B
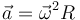 .
.
- C
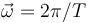 .
.
- D
 .
.
- A
- Solución
La respuesta correcta es la D.
7 Movimiento en polares
La velocidad de una partícula, expresada en coordenadas polares, tiene la expresión

con A y B dos constantes positivas. El movimiento de esta partícula es…
- A circular.
- B espiral, alejándose del origen.
- C rectilíneo.
- D espiral, acercándose al origen.
- Solución
La respuesta correcta es la B.





