última version al 13:10 20 sep 2018

1 Disco rodando sobre escuadra giratoria

Un disco (sólido "2") de masa $M$ y radio $R$ , rueda sin deslizar sobre una escuadra (sólido "0") de masa despreciable. La escuadra gira en el plano $O X 1 Y 1$ con velocidad angular constante $ω 0$ .

Encuentra reducciones cinemáticas de todos los movimientos del problema en el centro del disco $G$ .
Calcula el momento cinético del disco respecto a $G$ y $O$ , su energía cinética y su energía potencial.
Aplicando los métodos de la Mecánica Vectorial, encuentra las ecuaciones de movimiento del disco. ¿Cuál es la frecuencia propia de oscilación del sistema (también llamada frecuencia natural)?
Encuentra las fuerzas y momentos que actúan sobre la escuadra (sólido "0") para que se mueva de la forma descrita.

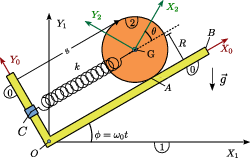
2 Barra rotando alrededor de barra horizontal con muelle

Una barra de longitud $2 d$ y masa despreciable (sólido "0") puede rotar alrededor del eje $O Z 1$ . El punto $O$ de la barra es fijo. La barra "0" siempre está contenida en el plano $O X 1 Y 1$ . Otra barra, también de longitud $2 d$ y masa $m$ (sólido "2"), está conectada a la barra "0" por un pasador en el punto $A$ . El pasador desliza sobre la barra "0". Además, la barra "2" gira alrededor de la barra "0". Un muelle de constante elástica $k$ y longitud natural nula $l 0 = d$ conecta los puntos $O$ y $A$ .

Determina las reducciones cinemáticas ${01},{20}$ y ${21}$ en $G$ .
Calcula el momento cinético de la barra "2" respecto de $G$ .
A partir de ahora suponemos que 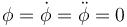$\phi=\dot{\phi}=\ddot{\phi}=0$ , es decir, la coordenada $φ$ ya no es un grado de libertad. Escribe las ecuaciones de Lagrange del sistema.
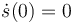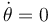En $t = 0$ tenemos $s (0) = d$ , $θ(0) = - π / 2$ , $\dot{s}(0)=0$ y $\dot{\theta}=0$ ( $φ$ sigue estando fijada). La barra "2" recibe una percusión $\vec{\hat{F}} = [\hat{F}_0, 0, \hat{F}_0]_1$ en el punto B. Determina el estado del sistema justo después de la percusión.

@@ Línea 1: / Línea 1: @@
+=[[ Sep. 2018 (M.R.) Disco rodando sobre escuadra giratoria | Disco rodando sobre escuadra giratoria]]=
+[[Archivo:MR_disco_escuadra_enunicado.png|right]]
+Un disco (sólido "2") de masa <math>M</math> y radio <math>R</math>, rueda sin deslizar sobre una escuadra (sólido "0") de masa despreciable. La escuadra gira en el plano
+<math>OX_1Y_1</math> con velocidad angular constante <math>\omega_0</math>.
+#Encuentra reducciones cinemáticas de todos los movimientos del problema en el centro del disco <math>G</math>.
+#Calcula el momento cinético del disco respecto a <math>G</math> y <math>O</math>, su energía cinética y su energía potencial.
+#Aplicando los métodos de la Mecánica Vectorial, encuentra las ecuaciones de movimiento del disco. ¿Cuál es la frecuencia propia de oscilación del sistema (también llamada frecuencia natural)?
+#Encuentra las fuerzas y momentos que actúan sobre la escuadra (sólido "0") para que se mueva de la forma descrita.
 =[[ Sep. 2018 (M.R.) Barra rotando alrededor de barra horizontal con muelle | Barra rotando alrededor de barra horizontal con muelle]]=
+[[Imagen:MR_2018_barras_muelle_enunciado.png|right]]
 Una barra de longitud <math>2d</math> y masa despreciable (sólido "0") puede rotar alrededor del eje <math>OZ_1</math>.  El punto <math>O</math> de la barra es fijo. La barra "0" siempre está contenida en el plano <math>OX_1Y_1</math>. Otra barra, también de longitud <math>2d</math> y masa <math>m</math> (sólido "2"), está conectada a la barra "0" por un pasador en el punto <math>A</math>. El pasador desliza sobre la barra "0". Además, la barra "2" gira alrededor de la barra "0". Un muelle de constante elástica <math>k</math> y longitud natural nula <math>l_0=d</math> conecta los puntos <math>O</math> y <math>A</math>.

Segunda Convocatoria 2017/18 (MR G.I.C.)

De Laplace

última version al 13:10 20 sep 2018

1 Disco rodando sobre escuadra giratoria

2 Barra rotando alrededor de barra horizontal con muelle

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES