Superposición de ondas
De Laplace
(→Misma amplitud) |
(→Misma amplitud) |
||
| Línea 18: | Línea 18: | ||
<center><math>y_1 = A_0\cos(\omega t - k x)\,</math>{{qquad}}{{qquad}} <math>y_2 = A_0\cos(\omega t - k x+\phi)\,</math></center> | <center><math>y_1 = A_0\cos(\omega t - k x)\,</math>{{qquad}}{{qquad}} <math>y_2 = A_0\cos(\omega t - k x+\phi)\,</math></center> | ||
| + | |||
| + | donde hemos tomado la primera señal como referencia y con desfase 0. A menudo, para hablar del desfase entre las dos ondas, en lugar del ángulo <math>\phi</math> se emplea la distancia <math>\Delta x</math> entre un máximo de una onda y el máximo de la otra, de forma que se habla de que están desfasadas “media longitud de onda” o “un cuarto de longitud de onda”, por ejemplo. La relación entre este desfase y el ángulo <math>\phi</math> es | ||
| + | |||
| + | <center><math>\frac{\Delta x}{\lambda}=\frac{\phi}{2\pi}</math></center> | ||
Para estas dos señales, la superposición será | Para estas dos señales, la superposición será | ||
| Línea 34: | Línea 38: | ||
<center><math>A(\phi) = 2A_0\cos\left(\frac{\phi}{2}\right)\qquad\qquad\phi'=\frac{\phi}{2}</math></center> | <center><math>A(\phi) = 2A_0\cos\left(\frac{\phi}{2}\right)\qquad\qquad\phi'=\frac{\phi}{2}</math></center> | ||
| + | |||
| + | Podemos interpretar este resultado de forma sencilla: la suma de dos ondas viajeras en el mismo sentido con la misma frecuencia y amplitud es una nueva onda viajera con un desfase que es la media de los desfases respectivos y cuya amplitud depende del desfase. | ||
| + | |||
| + | |||
| + | Atendiendo al valor del desfase tenemos dos casos importantes: | ||
| + | |||
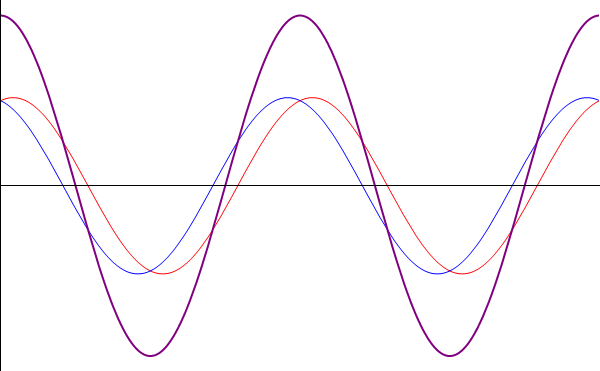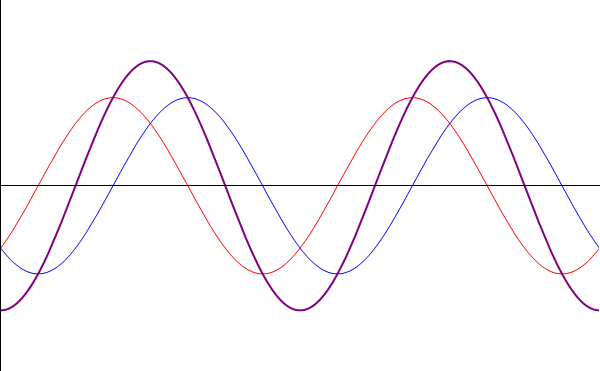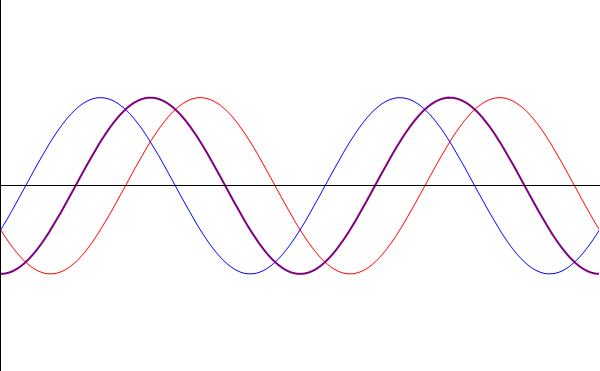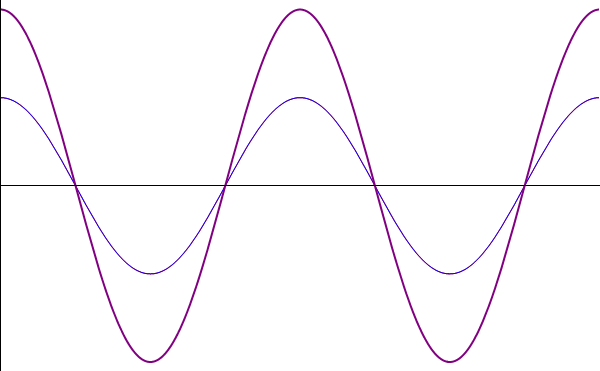
| + | * '''Interferencia constructiva:''' Cuando el desfase entre las ondas es un múltiplo par de <math>\pi</math> | ||
| + | |||
| + | * '''Interferencia destructiva:''' Cuando el desfase entre las ondas es un múltiplo impar de <math>\pi</math> | ||
====Diferente amplitud==== | ====Diferente amplitud==== | ||
Revisión de 21:10 25 feb 2009
Contenido |
1 Introducción
Una de las propiedades de la ecuación de onda es que se trata de una ecuación lineal, esto quiere decir que admite el principio de superposición. Esto significa que si y1 e y2 son las soluciones de la misma ecuación de onda
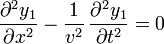
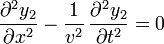
(esto es, ambas representan posibles ondas que se pueden propagar por la misma cuerda), entonces su suma también es solución
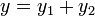

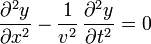
En el caso de ondas sinusoidales, el principio es el mismo. Sin embargo, dado que estas ondas se extienden 8en teoría) indefinidamente en el espacio, la coincidencia se produce en todas partes todo el tiempo. Además, la forma de las ondas resultantes a menudo posee interpretación por sí misma. Por ello, interesa estudiar el resultado de la superposición de ondas armónicas, y no solo considerarlas como compuestas de sus ondas componentes (que a menudo son desconocidas o irrelevantes, pues lo que se observa es el resultado de la superposición.
2 Mismo sentido
2.1 Misma frecuencia
2.1.1 Misma amplitud
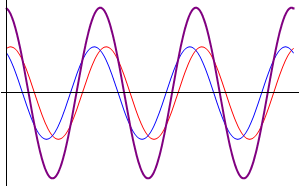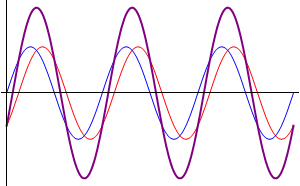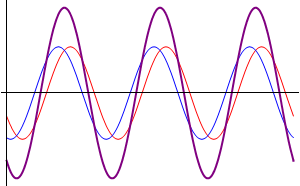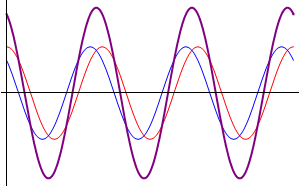
Comenzamos suponiendo el caso más sencillo posible: dos ondas que se propagan por la misma cuerda en el mismo sentido, con la misma frecuencia y la misma amplitud, diferenciándose exclusivamente en su desfase. Podremos escribir estas dos señales como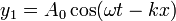
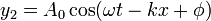
donde hemos tomado la primera señal como referencia y con desfase 0. A menudo, para hablar del desfase entre las dos ondas, en lugar del ángulo φ se emplea la distancia Δx entre un máximo de una onda y el máximo de la otra, de forma que se habla de que están desfasadas “media longitud de onda” o “un cuarto de longitud de onda”, por ejemplo. La relación entre este desfase y el ángulo φ es
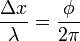
Para estas dos señales, la superposición será
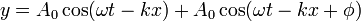
Aplicando aquí la relación trigonométrica que transforma sumas en productos
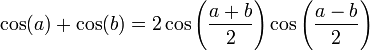
la superposición de ondas se nos convierte en
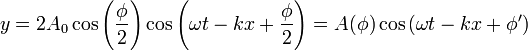
con
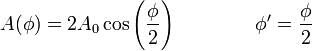
Podemos interpretar este resultado de forma sencilla: la suma de dos ondas viajeras en el mismo sentido con la misma frecuencia y amplitud es una nueva onda viajera con un desfase que es la media de los desfases respectivos y cuya amplitud depende del desfase.
Atendiendo al valor del desfase tenemos dos casos importantes:
- Interferencia constructiva: Cuando el desfase entre las ondas es un múltiplo par de π
- Interferencia destructiva: Cuando el desfase entre las ondas es un múltiplo impar de π