Superposición de ondas
De Laplace
(→Introducción) |
(→Introducción) |
||
| Línea 7: | Línea 7: | ||
<center><math>y=y_1+y_2\,</math>{{tose}}<math>\frac{\partial^2y}{\partial x^2}-\frac{1}{v^2}\,\frac{\partial^2y}{\partial t^2}=0</math></center> | <center><math>y=y_1+y_2\,</math>{{tose}}<math>\frac{\partial^2y}{\partial x^2}-\frac{1}{v^2}\,\frac{\partial^2y}{\partial t^2}=0</math></center> | ||
| + | |||
| + | [[Imagen:viajera3.gif|right]][[Imagen:Estacio2.gif|right]]Esto se aplica cualquiera que sean las ondas componentes. En el caso particular de pulsos de onda el resultado es que, aunque durante el periodo de coincidencia, la deformación de la cuerda puede adoptar formas extrañas, cuando se separan ambos pulsos continúan sin haber sido afectados en absoluto por la “colisión” con el otro. | ||
| + | |||
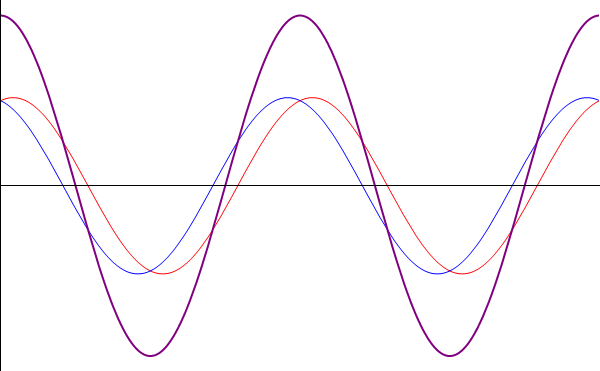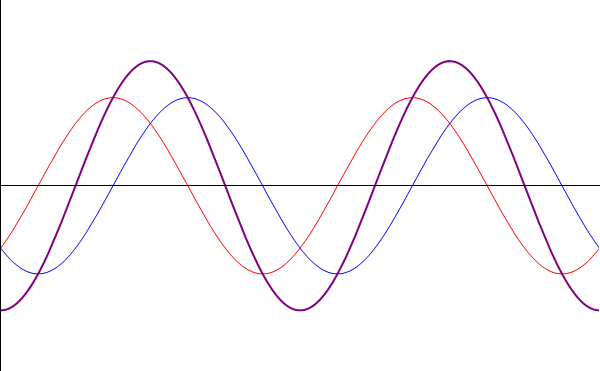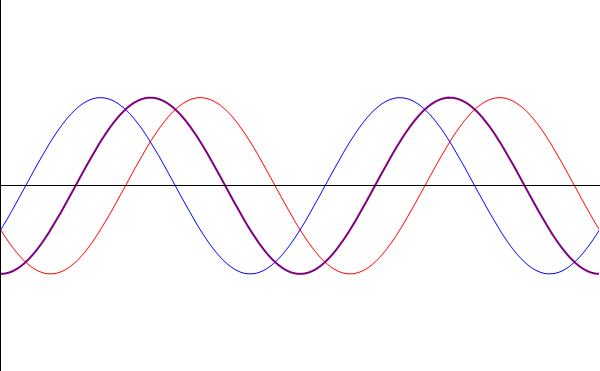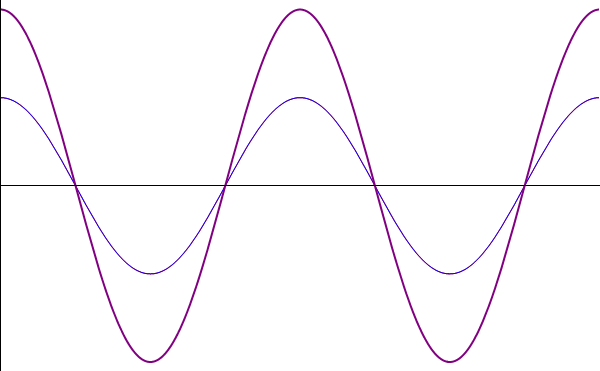
| + | En el caso de ondas sinusoidales, el principio es el mismo. Sin embargo, dado que estas ondas se extienden 8en teoría) indefinidamente en el espacio, la coincidencia se produce en todas partes todo el tiempo. Además, la forma de las ondas resultantes a menudo posee interpretación por sí misma. Por ello, interesa estudiar el resultado de la superposición de ondas armónicas, y no solo considerarlas como compuestas de sus ondas componentes (que a menudo son desconocidas o irrelevantes, pues lo que se observa es el resultado de la superposición. | ||
==Mismo sentido== | ==Mismo sentido== | ||
Revisión de 18:01 25 feb 2009
Contenido |
1 Introducción
Una de las propiedades de la ecuación de onda es que se trata de una ecuación lineal, esto quiere decir que admite el principio de superposición. Esto significa que si y1 e y2 son las soluciones de la misma ecuación de onda
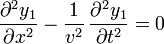
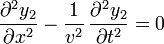
(esto es, ambas representan posibles ondas que se pueden propagar por la misma cuerda), entonces su suma también es solución
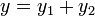

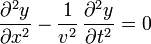
En el caso de ondas sinusoidales, el principio es el mismo. Sin embargo, dado que estas ondas se extienden 8en teoría) indefinidamente en el espacio, la coincidencia se produce en todas partes todo el tiempo. Además, la forma de las ondas resultantes a menudo posee interpretación por sí misma. Por ello, interesa estudiar el resultado de la superposición de ondas armónicas, y no solo considerarlas como compuestas de sus ondas componentes (que a menudo son desconocidas o irrelevantes, pues lo que se observa es el resultado de la superposición.