Plataforma sobre cilindro hueco rodante (GIE)
De Laplace
| (Una edición intermedia no se muestra.) | |||
| Línea 8: | Línea 8: | ||
<center>[[Archivo:inercia-triangulo-a.png|600px]]</center> | <center>[[Archivo:inercia-triangulo-a.png|600px]]</center> | ||
==Posición del centro de masas== | ==Posición del centro de masas== | ||
| + | Si etiquetamos como “1” al cateto OA, “2” el cateto OB y “3” la hipotenusa AB, las respectivas masas valen | ||
| + | |||
| + | <center><math>\begin{array}{rcl}m_1&=&3.75\times 0.60=2.25\,\mathrm{kg} \\ | ||
| + | m_2&=&3.75\times 0.80=3.00\,\mathrm{kg} \\ | ||
| + | m_3&=&3.75\times 0.60=3.75\,\mathrm{kg} \end{array}</math></center> | ||
| + | |||
| + | siendo la masa total | ||
| + | |||
| + | <center><math>m=m_1+m_2+m_3=9.00\,\mathrm{kg}</math></center> | ||
| + | |||
| + | Los centros de masas de las varillas se halla en sus respectivos centros | ||
| + | <center><math>\begin{array}{rcl}\overrightarrow{OG}_1&=&0.30\vec{\imath}\,\mathrm{m} \\ | ||
| + | \overrightarrow{OG}_2&=&0.40\vec{\jmath}\,\mathrm{m} \\ | ||
| + | \overrightarrow{OG}_3&=&0.30\vec{\imath}+0.40\vec{\jmath}\,\mathrm{m} \end{array}</math></center> | ||
| + | |||
| + | El centro de masas del conjunto es la media ponderada de estos tres, como si cada lado estuviera concentrado en su CM | ||
| + | |||
| + | <center><math>\overrightarrow{OG}=\frac{m_1\overrightarrow{OG}_1+m_2\overrightarrow{OG}_2+m_3\overrightarrow{OG}_3}{m}=0.20\vec{\imath}+0.30\vec{\jmath}</math></center> | ||
==Momento de inercia respecto a OZ== | ==Momento de inercia respecto a OZ== | ||
| + | El momento de inercia es la suma de los de las tres varillas por separado. | ||
| + | |||
| + | Para el cateto OA, el eje OZ es perpendicular por su extremo | ||
| + | |||
| + | <center><math>I_{O1}=\frac{1}{3}m_1 b_1^2 = 0.27\,\mathrm{kg}\cdot\mathrm{m}^2</math></center> | ||
| + | |||
| + | Lo mismo para el cateto OB | ||
| + | |||
| + | <center><math>I_{O2}=\frac{1}{3}m_2 b_2^2 = 0.64\,\mathrm{kg}\cdot\mathrm{m}^2</math></center> | ||
| + | |||
| + | Para la hipotenusa AB aplicamos el teorema de Steiner, teninedo en cuenta la posición de su centro <math>G_3</math> | ||
| + | |||
| + | <center><math>I_{O3}=\frac{1}{12}m_3b_3^2+m_3|\overrightarrow{OG}_3|^2=1.25\,\mathrm{kg}\cdot\mathrm{m}^2</math></center> | ||
| + | |||
| + | siendo el momento de inercia total la suma de estos tres | ||
| + | |||
| + | <center><math>I_O= 2.16\,\mathrm{kg}\cdot\mathrm{m}^2</math></center> | ||
| + | |||
==Momento de inercia respecto a GZ== | ==Momento de inercia respecto a GZ== | ||
| + | Aplicamos el teorema de Steiner | ||
| + | |||
| + | <center><math>I_O=I_G+m|\overrightarrow{OG}|^2\qquad\Rightarrow\qquad I_G = 2.16-9.00(0.20^2+0.30^2)=0.99\,\mathrm{kg}\cdot\mathrm{m}^2</math></center> | ||
==Velocidad del triángulo== | ==Velocidad del triángulo== | ||
| + | Por conservación de la energía mecánica | ||
| + | |||
| + | <center><math>\frac{1}{2}I_O|\vec{\omega}|^2 = m g \Delta h_G</math></center> | ||
| + | |||
| + | siendo <math>\Delta h_G</math> lo que desciende el centro de masas. Pasa de estar a 30cm de altura a estar 20cm por debajo del eje. Por tanto | ||
| + | |||
| + | <center><math>\frac{1}{2}2.16|\vec{\omega}|^2 = 9.00\times 10\times 0.50\qquad\Rightarrow\qquad |\vec{\omega}| = 6.45\,\frac{\mathrm{rad}}{\mathrm{s}}</math></center> | ||
última version al 17:52 8 sep 2018
Contenido |
1 Enunciado
Un sólido de forma triangular está formado por tres varillas de 0.60 m, 0.80 m y 1.00 m, soldadas formando un triángulo rectángulo OAB. La densidad lineal de masa de las tres varillas es la misma: μ=3.75 kg/m. Empleamos un sistema de ejes tal que el vértice entre los dos catetos es el origen y los ejes OX y OY son paralelos a los catetos, como en la figura de la izquierda
- Determine la posición de G, el centro de masas del sólido.
- Calcule el momento de inercia del triángulo respecto al eje OZ, perpendicular al plano del triángulo por el punto O.
- Calcule el momento de inercia respecto al eje GZ, paralelo a OZ por el centro de masas.
- Suponga que el triángulo se sitúa en un plano vertical, con su cateto corto horizontal y el largo, vertical y por arriba. El triángulo se articula en O a un punto fijo. Se sujeta en reposo y entonces se suelta. ¿Qué velocidad angular posee en el instante en el que el cateto largo pasa por la horizontal?

2 Posición del centro de masas
Si etiquetamos como “1” al cateto OA, “2” el cateto OB y “3” la hipotenusa AB, las respectivas masas valen

siendo la masa total
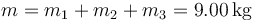
Los centros de masas de las varillas se halla en sus respectivos centros

El centro de masas del conjunto es la media ponderada de estos tres, como si cada lado estuviera concentrado en su CM

3 Momento de inercia respecto a OZ
El momento de inercia es la suma de los de las tres varillas por separado.
Para el cateto OA, el eje OZ es perpendicular por su extremo

Lo mismo para el cateto OB

Para la hipotenusa AB aplicamos el teorema de Steiner, teninedo en cuenta la posición de su centro G3
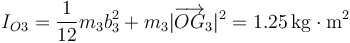
siendo el momento de inercia total la suma de estos tres

4 Momento de inercia respecto a GZ
Aplicamos el teorema de Steiner

5 Velocidad del triángulo
Por conservación de la energía mecánica
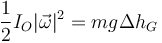
siendo ΔhG lo que desciende el centro de masas. Pasa de estar a 30cm de altura a estar 20cm por debajo del eje. Por tanto






