Percusión en sistema de dos masas
De Laplace
| Línea 1: | Línea 1: | ||
==Enunciado== | ==Enunciado== | ||
| - | Supongamos dos masas iguales <math>m/2</math> unidas por una barra rígida de longitud <math> | + | Supongamos dos masas iguales <math>m/2</math> unidas por una barra rígida de longitud <math>2b</math>, sin masa (lo que sería una mancuerna ideal). Las masas reposan sobre un plano horizontal, sobre el que pueden moverse sin rozamiento. |
Inicialmente la varilla está en reposo. | Inicialmente la varilla está en reposo. | ||
# Se comunica una percusión <math>\vec{P}</math> perpendicular a la barra en un punto A a una distancia <math>c</math> de su centro. ¿Cuánto valen la cantidad de movimiento, el momento cinético respecto al CM y la energía cinética de la barra? ¿Cómo es el movimiento del sistema a partir de ese momento? | # Se comunica una percusión <math>\vec{P}</math> perpendicular a la barra en un punto A a una distancia <math>c</math> de su centro. ¿Cuánto valen la cantidad de movimiento, el momento cinético respecto al CM y la energía cinética de la barra? ¿Cómo es el movimiento del sistema a partir de ese momento? | ||
| - | # ¿Cómo cambian los resultados del problema anterior si en lugar de una mancuerna tenemos una barra homogénea de longitud <math> | + | # ¿Cómo cambian los resultados del problema anterior si en lugar de una mancuerna tenemos una barra homogénea de longitud <math>2b</math> y masa <math>m</math> a la cual se comunica una percusión <math>\vec{P}</math> perpendicular a la barra a una distancia <math>c</math> de su centro? |
| - | # ¿Cómo cambian los resultados de los dos problemas anteriores si la barra está articulada a un punto fijo B, situado a una distancia d del centro de la barra? ¿Cuánto valen las fuerzas y momentos de reacción en B? | + | # ¿Cómo cambian los resultados de los dos problemas anteriores si la barra está articulada a un punto fijo <math>B</math>, situado a una distancia <math>d</math> del centro de la barra? ¿Cuánto valen las fuerzas y momentos de reacción en B? |
# ¿Y sí en lugar de estar articulada, está empotrada en B? | # ¿Y sí en lugar de estar articulada, está empotrada en B? | ||
| Línea 23: | Línea 23: | ||
Para la rotación necesitamos en primer lugar el tensor de inercia del sistema en O. En este caso es muy simple, los tres ejes son principales; el momento respecto a OX es nulo por estar las dos masas sobre el propio eje; el momento respecto a OY es igual al momento respecto a OZ y vale | Para la rotación necesitamos en primer lugar el tensor de inercia del sistema en O. En este caso es muy simple, los tres ejes son principales; el momento respecto a OX es nulo por estar las dos masas sobre el propio eje; el momento respecto a OY es igual al momento respecto a OZ y vale | ||
| - | <center><math>I_{yy}=I_{zz}=\frac{m}{2} | + | <center><math>I_{yy}=I_{zz}=\frac{m}{2}b^2 + \frac{m}{2}b^2 = mb^2</math></center> |
El momento cinético del sólido es entonces, en este sistema de ejes principales | El momento cinético del sólido es entonces, en este sistema de ejes principales | ||
| - | <center><math>\vec{L}_O=I_{xx}\omega_x\vec{\imath}+I_{yy}\omega_y\vec{\jmath}+I_{zz}\omega_z\vec{k}= | + | <center><math>\vec{L}_O=I_{xx}\omega_x\vec{\imath}+I_{yy}\omega_y\vec{\jmath}+I_{zz}\omega_z\vec{k}=mb^2\left(\omega_y\vec{\jmath}+I_{zz}\omega_z\vec{k}\right)</math></center> |
El momento de percusión vale | El momento de percusión vale | ||
| Línea 35: | Línea 35: | ||
igualando resulta | igualando resulta | ||
| - | <center><math>\omega_y=0\qquad\qquad \omega_z=\frac{ | + | <center><math>\omega_y=0\qquad\qquad \omega_z=\frac{cP}{mb^2}\vec{k}</math></center> |
Una vez que se efectúa la percusión la velocidad del CM y la velocidad angular permanecen constantes, por lo que el movimiento de la varilla es una combinación de avance horizontal y de rotación respecto a un eje vertical. | Una vez que se efectúa la percusión la velocidad del CM y la velocidad angular permanecen constantes, por lo que el movimiento de la varilla es una combinación de avance horizontal y de rotación respecto a un eje vertical. | ||
| Línea 45: | Línea 45: | ||
en este caso O es el propio CM por lo que su velocidad ya la hemos calculado. Esto nos da | en este caso O es el propio CM por lo que su velocidad ya la hemos calculado. Esto nos da | ||
| - | <center><math>\overrightarrow{OI}=\frac{P/m\vec{k}\times\vec{\jmath}}{ | + | <center><math>\overrightarrow{OI}=\frac{(P/m)\vec{k}\times\vec{\jmath}}{cP/mb^2}=-\frac{b^2}{c}\vec{\imath}</math></center> |
| - | Si c es nula, este CIR se va al infinito, lo que corresponde a que si golpeamos la varilla en el centro no gira, sino que solo se traslada. Si golpeamos en una de las masas (<math>c=b | + | Si c es nula, este CIR se va al infinito, lo que corresponde a que si golpeamos la varilla en el centro no gira, sino que solo se traslada. Si golpeamos en una de las masas (<math>c=b</math>) el CIR pasa a estar en la otra, que en el instante inicial aun no se mueve. |
==Barra homogénea, libre== | ==Barra homogénea, libre== | ||
| + | En el caso de una masa homogénea, el razonamiento es el mismo que en el apartado anterior. La única diferencia es que el momento de inercia es ahora | ||
| + | |||
| + | <center><math>I_{yy}=I_{zz}=\frac{1}{12}m(2b)^2 = \frac{mb^2}{3}</math></center> | ||
| + | |||
| + | lo que produce una velocidad angular diferente | ||
| + | |||
| + | <center><math>\omega_y=0\qquad\qquad \omega_z=\frac{3P}{mb^2}\vec{k}</math></center> | ||
| + | |||
| + | aunque la velocidad del CM no se ve afectada | ||
| + | |||
| + | <center><math>\Delta (m \vec{v}_G)=m\vec{v}^+_G =P\vec{\jmath}\qquad\Rightarrow\qquad \vec{v}^+_G=\frac{P}{m}\vec{\jmath}</math></center> | ||
| + | |||
| + | Esto implica que el nuevo centro instantáneo de rotación se halla en | ||
| + | |||
| + | <center><math>\overrightarrow{OI}=\frac{(P/m)\vec{k}\times\vec{\jmath}}{3cP/mb^2}=-\frac{b^2}{3c}\vec{\imath}</math></center> | ||
| + | |||
| + | Esto quiere decir que si se aplica la percusión en un extremo, el centro instantáneo de rotación se halla a b/3 del centro, es decir, 1 1/6 de la longitud de la barra desde el centro (y por tanto, a 1/3 desde el extremo). | ||
| + | |||
| + | |||
==Barra con masas, articulada== | ==Barra con masas, articulada== | ||
| + | Si la barra está articulada en B, quiere decir que la velocidad de este punto es nula en todo instante | ||
| + | |||
| + | <center><math>\vec{v}_B=\vec{0}</math></center> | ||
| + | |||
| + | Esta velocidad es, en general, incompatible con el campo de velocidades hallado en el primer apartado, por lo que el movimiento antes calculado no es posible en este caso. | ||
| + | |||
| + | El vínculo de la articulación implica la aparición de una fuerza de reacción impulsiva en este punto. Al ser una articulación no aparece un par en B, ya que la rotación es libre alrededor de este punto. La ecuación para la velocidad del CM es ahora | ||
| + | |||
| + | <center><math>m\vec{v}^+_G = \vec{P}+\vec{P}_r </math></center> | ||
| + | |||
| + | donde la percusión de reacción es una incógnita más del problema.Esº | ||
| + | |||
| + | Esta ecuación, por tanto, no es suficiente para determinar la velocidad del CM. | ||
| + | |||
| + | Podemos aplicar que B es un punto fijo y calcular momentos respecto a este punto, de manera que | ||
| + | |||
| + | <center><math>\Delta \vec{L}_B=\overrightarrow{BA}\times\vec{P} </math></center> | ||
| + | |||
| + | aquí no aparece la percusión de reacción porque se aplica en el propio punto B y por tanto su momento es nulo. | ||
| + | |||
| + | El momento de inercia respecto a este punto lo podemos hallar por el teorema de Steiner | ||
| + | |||
| + | <center><math>I_{xx}=0\qquad\qquad I_{yy}=I_{zz}=mb^2+md^2 </math></center> | ||
| + | |||
| + | por lo que la ecuación para la rotación queda | ||
| + | |||
| + | <center><math>m(b^2+d^2(\omega_y\vec{\jmath}+\omega_z\vec{k}) = ((c+d)\vec{\imath})\times(P\vec{\jmath})\qquad \qquad\omega_y=0\qquad\qquad \omega_z=\frac{(c+d)P}{m(b^2+d^2)}</math></center> | ||
| + | |||
| + | Por tanto, la barra comienza a describir u movimiento de rotación alrededor de B con esta velocidad angular. | ||
==Barra homogénea, articulada== | ==Barra homogénea, articulada== | ||
==Barra con masas, empotrada== | ==Barra con masas, empotrada== | ||
==Barra homogénea, empotrada== | ==Barra homogénea, empotrada== | ||
Revisión de 23:49 28 ago 2018
Contenido |
1 Enunciado
Supongamos dos masas iguales m / 2 unidas por una barra rígida de longitud 2b, sin masa (lo que sería una mancuerna ideal). Las masas reposan sobre un plano horizontal, sobre el que pueden moverse sin rozamiento.
Inicialmente la varilla está en reposo.
- Se comunica una percusión
 perpendicular a la barra en un punto A a una distancia c de su centro. ¿Cuánto valen la cantidad de movimiento, el momento cinético respecto al CM y la energía cinética de la barra? ¿Cómo es el movimiento del sistema a partir de ese momento?
perpendicular a la barra en un punto A a una distancia c de su centro. ¿Cuánto valen la cantidad de movimiento, el momento cinético respecto al CM y la energía cinética de la barra? ¿Cómo es el movimiento del sistema a partir de ese momento?
- ¿Cómo cambian los resultados del problema anterior si en lugar de una mancuerna tenemos una barra homogénea de longitud 2b y masa m a la cual se comunica una percusión
 perpendicular a la barra a una distancia c de su centro?
perpendicular a la barra a una distancia c de su centro?
- ¿Cómo cambian los resultados de los dos problemas anteriores si la barra está articulada a un punto fijo B, situado a una distancia d del centro de la barra? ¿Cuánto valen las fuerzas y momentos de reacción en B?
- ¿Y sí en lugar de estar articulada, está empotrada en B?
2 Barra con masas, libre
Las ecuaciones básicas de la dinámica del sólido sometido a una percusión aplicada en un punto A son

De la primera obtenemos la velocidad del centro de masas tras la percusión (antes de ella es nula). Aquí m es la masa total del sólido (la masa de cada partícula es m/2).
Tomamos un sistema de ejes en el que el OX es colineal con la barra, el OY es ortogonal a ella dentro del mismo plano horizontal y el OZ es perpendicular al plano del movimiento.
En este sistema

Para la rotación necesitamos en primer lugar el tensor de inercia del sistema en O. En este caso es muy simple, los tres ejes son principales; el momento respecto a OX es nulo por estar las dos masas sobre el propio eje; el momento respecto a OY es igual al momento respecto a OZ y vale
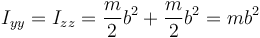
El momento cinético del sólido es entonces, en este sistema de ejes principales
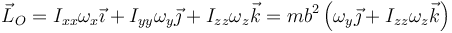
El momento de percusión vale
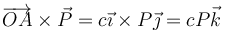
igualando resulta

Una vez que se efectúa la percusión la velocidad del CM y la velocidad angular permanecen constantes, por lo que el movimiento de la varilla es una combinación de avance horizontal y de rotación respecto a un eje vertical.
El centro instantáneo de rotación de este movimiento plano es

en este caso O es el propio CM por lo que su velocidad ya la hemos calculado. Esto nos da
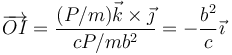
Si c es nula, este CIR se va al infinito, lo que corresponde a que si golpeamos la varilla en el centro no gira, sino que solo se traslada. Si golpeamos en una de las masas (c = b) el CIR pasa a estar en la otra, que en el instante inicial aun no se mueve.
3 Barra homogénea, libre
En el caso de una masa homogénea, el razonamiento es el mismo que en el apartado anterior. La única diferencia es que el momento de inercia es ahora
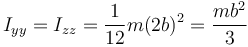
lo que produce una velocidad angular diferente
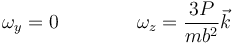
aunque la velocidad del CM no se ve afectada

Esto implica que el nuevo centro instantáneo de rotación se halla en
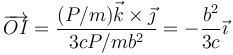
Esto quiere decir que si se aplica la percusión en un extremo, el centro instantáneo de rotación se halla a b/3 del centro, es decir, 1 1/6 de la longitud de la barra desde el centro (y por tanto, a 1/3 desde el extremo).
4 Barra con masas, articulada
Si la barra está articulada en B, quiere decir que la velocidad de este punto es nula en todo instante
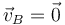
Esta velocidad es, en general, incompatible con el campo de velocidades hallado en el primer apartado, por lo que el movimiento antes calculado no es posible en este caso.
El vínculo de la articulación implica la aparición de una fuerza de reacción impulsiva en este punto. Al ser una articulación no aparece un par en B, ya que la rotación es libre alrededor de este punto. La ecuación para la velocidad del CM es ahora
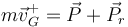
donde la percusión de reacción es una incógnita más del problema.Esº
Esta ecuación, por tanto, no es suficiente para determinar la velocidad del CM.
Podemos aplicar que B es un punto fijo y calcular momentos respecto a este punto, de manera que
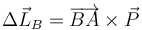
aquí no aparece la percusión de reacción porque se aplica en el propio punto B y por tanto su momento es nulo.
El momento de inercia respecto a este punto lo podemos hallar por el teorema de Steiner
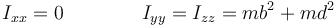
por lo que la ecuación para la rotación queda
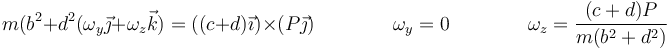
Por tanto, la barra comienza a describir u movimiento de rotación alrededor de B con esta velocidad angular.





