Corriente eléctrica
De Laplace
(→Problemas) |
(→Densidades de corriente e intensidad de corriente) |
||
| Línea 1: | Línea 1: | ||
==Introducción== | ==Introducción== | ||
==Densidades de corriente e intensidad de corriente== | ==Densidades de corriente e intensidad de corriente== | ||
| + | ===Densidad volumétrica de corriente=== | ||
| + | En situaciones no estáticas, las cargas que forman un sistema se encuentran en movimiento. Aunque todas las cargas que forman un material se encuentran en constante agitación, sólo una parte de ellas (los llamados ''portadores de carga'' poseen una velocidad promedio distinta de cero. La magnitud macroscópica que describe este movimiento colectivo es la \emph{densidad de corriente}, definida como | ||
| + | |||
| + | <center><math>\mathbf{J} = \frac{1}{\Delta\tau}\sum_{q_i\in \Delta\tau} q_i\mathbf{v}_i</math></center> | ||
| + | |||
| + | siendo su unidad en el SI 1 A/m². | ||
| + | |||
| + | Esta densidad de corriente no tiene una relación directa con la densidad de carga, ya que es perfectamente posible que en un punto de un conductor la densidad de carga se anule (porque haya tantas cargas positivas como negativas), mientras que la densidad de corriente sea distinta de cero (por ejemplo, porque las negativas se estén moviendo y las positivas no). Sí existe relación con la densidad de portadores. Dentro de un material en el cual existe movimiento de cargas por el desplazamiento de una o varias \emph{especies} (tipos de portadores, por ejemplo, en agua salada tendríamos al menos cuatro especies: OH<sup>−</sup>, H<sub>3</sub>O<sup>+</sup>, Cl<sup>−</sup>, Na<sup>+</sup>), la densidad de corriente puede escribirse como | ||
| + | |||
| + | <center><math>\mathbf{J} =\sum_i (Z_ie) N_i \mathbf{v}_i</math></center> | ||
| + | |||
| + | siendo <math>N_i</math> la densidad de cada especie, <math>\mathbf{v}_i</math> su velocidad neta promedio (o ''[[velocidad de arrastre]]'') y <math>Z_ie</math> su carga. En el caso común de un metal, en el que sólo los electrones se mueven <math>\mathbf{J} = -e | ||
| + | N_e\mathbf{v}_e</math>$. En un semiconductor tendremos un término debido a los electrones y otro debido a los huecos. | ||
| + | |||
| + | ===Densidad superficial de corriente=== | ||
| + | Del mismo modo que se define la densidad de corriente volumétrica también puede definirse la densidad de corriente superficial | ||
| + | |||
| + | <center><math>\mathbf{K} = \frac{1}{\Delta S}\sum_{q_i\in\Delta S} q_i\mathbf{v}_i</math></center> | ||
| + | |||
| + | Esta densidad será de interés cuando tengamos que los portadores de carga están concentrados en las superficies de los materiales. | ||
| + | |||
| + | ===Intensidad de corriente=== | ||
| + | Si consideramos el flujo de carga que atraviesa una determinada sección de un conductor, el resultado es la ''intensidad de corriente'' | ||
| + | |||
| + | <center><math>I = \int_S \mathbf{J}{\cdot}\mathrm{d}\mathbf{S}</math></center> | ||
| + | |||
| + | La intensidad de corriente, que se mide en amperios (A) en el SI, es un escalar con signo, indicando si el flujo es el sentido de la normal a la superficie o en el opuesto. | ||
| + | |||
| + | En el caso de una densidad de corriente superficial, puede obtenerse la intensidad de corriente que atraviesa una curva <math>\Gamma</math> (trazada sobre la superficie, y que es atravesada por la corriente) como | ||
| + | |||
| + | <math>I=\int_\Gamma \mathbf{K}{\cdot}\mathbf{n}_1\mathrm{d}l</math> | ||
| + | |||
| + | siendo <math>\mathbf{n}_1</math> un vector tangente a la superficie y normal a la curva <math>\Gamma</math>. | ||
| + | |||
==Ley de conservación de la carga== | ==Ley de conservación de la carga== | ||
==Ecuaciones del campo y de la corriente== | ==Ecuaciones del campo y de la corriente== | ||
Revisión de 12:25 25 feb 2009
1 Introducción
2 Densidades de corriente e intensidad de corriente
2.1 Densidad volumétrica de corriente
En situaciones no estáticas, las cargas que forman un sistema se encuentran en movimiento. Aunque todas las cargas que forman un material se encuentran en constante agitación, sólo una parte de ellas (los llamados portadores de carga poseen una velocidad promedio distinta de cero. La magnitud macroscópica que describe este movimiento colectivo es la \emph{densidad de corriente}, definida como
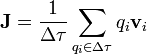
siendo su unidad en el SI 1 A/m².
Esta densidad de corriente no tiene una relación directa con la densidad de carga, ya que es perfectamente posible que en un punto de un conductor la densidad de carga se anule (porque haya tantas cargas positivas como negativas), mientras que la densidad de corriente sea distinta de cero (por ejemplo, porque las negativas se estén moviendo y las positivas no). Sí existe relación con la densidad de portadores. Dentro de un material en el cual existe movimiento de cargas por el desplazamiento de una o varias \emph{especies} (tipos de portadores, por ejemplo, en agua salada tendríamos al menos cuatro especies: OH−, H3O+, Cl−, Na+), la densidad de corriente puede escribirse como
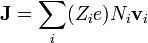
siendo Ni la densidad de cada especie,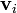 
su velocidad neta promedio (o velocidad de arrastre) y Zie su carga. En el caso común de un metal, en el que sólo los electrones se mueven 
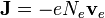$. En un semiconductor tendremos un término debido a los electrones y otro debido a los huecos.
2.2 Densidad superficial de corriente
Del mismo modo que se define la densidad de corriente volumétrica también puede definirse la densidad de corriente superficial
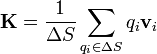
Esta densidad será de interés cuando tengamos que los portadores de carga están concentrados en las superficies de los materiales.
2.3 Intensidad de corriente
Si consideramos el flujo de carga que atraviesa una determinada sección de un conductor, el resultado es la intensidad de corriente
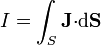
La intensidad de corriente, que se mide en amperios (A) en el SI, es un escalar con signo, indicando si el flujo es el sentido de la normal a la superficie o en el opuesto.
En el caso de una densidad de corriente superficial, puede obtenerse la intensidad de corriente que atraviesa una curva Γ (trazada sobre la superficie, y que es atravesada por la corriente) como
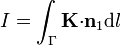
siendo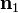 
un vector tangente a la superficie y normal a la curva Γ.
