Primera Convocatoria Ordinaria 2017/18 (F1 G.I.A.)

De Laplace

(Diferencias entre revisiones)

Revisión de 20:24 19 ago 2018

1 Partícula en movimiento con trayectoria y ley horaria conocidas

Una partícula $P$ se mueve respecto de un sistema de referencia cartesiano $O X Y Z$ , recorriendo la curva $Γ$ descrita por la ecuación paramétrica:

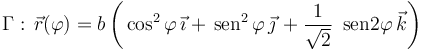
$\Gamma: \!\ \vec{r}(\varphi)= b\!\ \bigg(\cos^2 \varphi \!\ \vec{\imath}+\,\mathrm{sen}^2\, \varphi\!\ \vec{\jmath}\!\ +\frac{1}{\sqrt{2}}\ \,\mathrm{sen} 2\varphi\!\ \vec{k}\bigg)$

El movimiento de la partícula tiene lugar en el intervalo 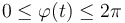$0\leq \varphi(t) \leq 2\pi$ , según la ley horaria 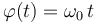$\varphi(t)=\omega_0\!\ t$ . Los parámetros $b$ y $ω 0$ tienen valores constantes conocidos.

Obtenga las expresiones de las componentes intrínsecas y cartesianas de la velocidad y la aceleración, en función del tiempo. Obtenga también la ley horaria 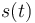$\displaystyle s(t)$ para el parámetro arco.

2 Cuerpo puntual sobre rampa con rozamiento y resorte

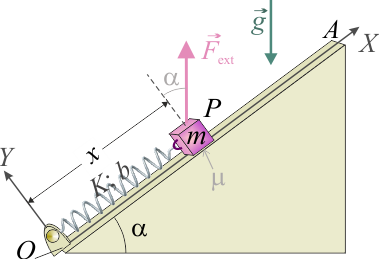
Un cuerpo que puede ser considerado como un punto material

P

de masa

m

, se encuentra en una rampa estrecha

O A

que forma con la horizontal un ángulo

α

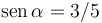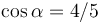tal que $\,\mathrm{sen}\,\alpha=3/5$ y $\,\mathrm{cos}\,\alpha=4/5$ . Entre partícula y rampa se establece un contacto unilateral; además, el contacto es rugoso, estando caracterizado por un coeficiente de rozamiento seco, que aproximadamente tiene el mismo valor, tanto para el caso estático como para el dinámico

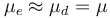$\mu_e\approx\mu_d=\mu$ . Un resorte de longitud natural $b$ y constante recuperadora $K$ conecta la partícula $P$ con el extremo fijo de la rampa, $O$ . Se sugiere utilizar un sistema de referencia cartesiano en que la rampa coincide con el eje $O X$ y el eje $O Y$ es perpendicular a la superficie $Σ$ de la misma. Los parámetros del sistema presentan valores tales que verifican la relación $\,mg=Kb$ .

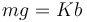Obtenga la posición de la rampa en que la partícula se mantendría en equilibrio, $P eq = P (x e q,0)$ , en el caso en que no hubiese rozamiento ( $μ = 0$ ). Calcule el valor de la reacción normal del plano-rampa sobre la partícula.
Analice el equilibrio del sistema en el caso de que exista rozamiento ( $\mu\neq 0$ ), y obtenga la expresión algebraica que permite determinar el rango de posiciones de equilibrio de la partícula en la rampa. ¿Cuál es dicho rango para el caso $μ = 1 / 2$ ?
Estando la partícula en el punto $O$ , se aplica una fuerza $\vec{F}_\mathrm{ext}$ , que en todo momento tiene la dirección y sentido opuesto al peso de la partícula para que ésta ascienda por la rampa; es decir, $\vec{F}_\mathrm{ext}=F(x)\!\ [(3/5)\!\ \vec{\imath}+(4/5)\!\ \vec{\jmath}]$ . ¿Cómo deber ser $F (x)$ para que la partícula se desplace a lo largo de la rampa con velocidad constante? ¿Cuál debe ser su valor máximo para que la partícula no pierda el contacto con la rampa?
Calcule el trabajo realizado por la fuerza $\vec{F}_\mathrm{ext}$ para llevar la partícula desde $O$ hasta el punto $P 0 = P (x 0,0)$ en que pierde el contacto con la rampa. ¿Y qué trabajo ha realizado la fuerza de rozamiento en el proceso?

@@ Línea 9: / Línea 9: @@
 El movimiento de la partícula tiene lugar en el intervalo <math>0\leq \varphi(t) \leq 2\pi</math>, según la ley horaria <math>\varphi(t)=\omega_0\!\ t</math>. Los parámetros <math>b</math> y <math>\omega_0</math> tienen valores constantes conocidos.
-&nbsp;
 Obtenga las expresiones de las componentes intrínsecas y cartesianas de la velocidad y la aceleración, en función del tiempo. Obtenga también la ley horaria <math>\displaystyle s(t)</math> para el parámetro arco.
 ==[[Cuerpo puntual sobre rampa con rozamiento y resorte, F1 GIA (Ene, 2018)|Cuerpo puntual sobre rampa con rozamiento y resorte]]==

Primera Convocatoria Ordinaria 2017/18 (F1 G.I.A.)

De Laplace

Revisión de 20:24 19 ago 2018

1 Partícula en movimiento con trayectoria y ley horaria conocidas

2 Cuerpo puntual sobre rampa con rozamiento y resorte

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES