Propiedades de una onda sinusoidal
De Laplace
(Diferencias entre revisiones)
(Nueva página: ==Enunciado== Una perturbación a lo largo de una cuerda se describe mediante la ecuación <center><math>y = 0.3\cos(126t-0.628x)\,</math></center> con ''x'' e ''y'' medidos en cen...) |
|||
| Línea 1: | Línea 1: | ||
==Enunciado== | ==Enunciado== | ||
| - | Una perturbación a lo largo de una cuerda se describe mediante la ecuación | + | [[Imagen:viajera.gif|left]]Una perturbación a lo largo de una cuerda se describe mediante la ecuación |
<center><math>y = 0.3\cos(126t-0.628x)\,</math></center> | <center><math>y = 0.3\cos(126t-0.628x)\,</math></center> | ||
| Línea 10: | Línea 10: | ||
==Solución== | ==Solución== | ||
| + | Esta función es una onda viajera correspondiente a la la forma general | ||
| + | |||
| + | <center><math>y = A \cos(\omega t - kx) = A \cos\left(k\left(x-vt\right)\right)\,</math></center> | ||
| + | |||
| + | que, por se de la forma <math>f(x-vt)</math> es claramente una solución de la ecuación de onda. | ||
===Amplitud=== | ===Amplitud=== | ||
===Frecuencia angular=== | ===Frecuencia angular=== | ||
Revisión de 16:51 23 feb 2009
Contenido |
1 Enunciado
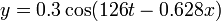
con x e y medidos en centímetros y t en segundos.
Para esta onda, halle su amplitud, frecuencia angular, periodo, número de onda y longitud de onda.
2 Solución
Esta función es una onda viajera correspondiente a la la forma general
que, por se de la forma f(x − vt) es claramente una solución de la ecuación de onda.
