Primera convocatoria 2017/18 (F2GIA)

De Laplace

Revisión de 18:43 9 jul 2018 (ver código fuente) Gabriel (Discusión | contribuciones) (→Campo eléctrico de distribución volumétrica de carga con simetría radial) ← Edición más antigua		Revisión de 18:44 9 jul 2018 (ver código fuente) Gabriel (Discusión | contribuciones) (→Campo eléctrico de distribución volumétrica de carga con simetría radial) Edición más nueva →
Línea 9:		Línea 9:
	# ¿Qué relación deben verificar la cantidades de <math>Q</math> y <math>q</math> de las respectivas cargas puntuales descritas en el sistema para que la fuerza eléctrica resultante que actúa sobre la carga que ocupa el punto <math>A</math> sea nula, <math>\vec{F}_e(Q;A)=\vec{0}</math>?		# ¿Qué relación deben verificar la cantidades de <math>Q</math> y <math>q</math> de las respectivas cargas puntuales descritas en el sistema para que la fuerza eléctrica resultante que actúa sobre la carga que ocupa el punto <math>A</math> sea nula, <math>\vec{F}_e(Q;A)=\vec{0}</math>?
	# En las condiciones del apartado anterior, ¿cómo es la fuerza eléctrica resultante que actúa sobre cada una de las otras tres cargas?		# En las condiciones del apartado anterior, ¿cómo es la fuerza eléctrica resultante que actúa sobre cada una de las otras tres cargas?
-
-	==[[Campo eléctrico de distribución volumétrica de carga con simetría radial (F2GIA)|Campo eléctrico de distribución volumétrica de carga con simetría radial]]==
-
-	En una esfera <math>\tau_0</math> de radio <math>R_0</math> y centro en <math>O</math>, existe una distribución no uniforme de carga eléctrica negativa descrita por una densidad volumétrica radial <math>\rho_e(r)</math>, respecto del punto <math>O</math>, de manera que <math>r</math> es la distancia desde dicho centro al punto <math>P</math> donde se mide la densidad de carga. Dicha distribuci'on es tal que si consideramos una región esférica <math>\tau</math> con centro en <math>O</math> y radio <math>r\leq R_0</math>, la cantidad parcial de carga contenida en <math>\tau</math> es <math>Q_\tau=-Q_0\!\ (r/R_0)^2=Q_\tau(r)</math>. No hay más cargas en el
-	sistema.
-
-	# ¿Cómo es la componente radial del campo eléctrico <math>E(r)</math> creado por la distribución descrita, tanto dentro como fuera de la esfera <math>\tau_0</math>?
-	# ¿Cómo es el potencial electrostático creado por la distribución en el exterior de <math>\tau_0</math>? ¿Cuánto vale el potencial en el centro <math>O</math>?

---

Revisión de 18:44 9 jul 2018

Fuerza eléctrica en sistema de cuatro cargas puntuales

Dos cargas eléctricas puntuales idénticas de valor Q, ocupan sendos puntos A y C que, en un sistema de referencia $OXYZ$, tienen coordenadas cartesianas A(a,0,0) y C( − a,0,0). Otras dos cargas idénticas entre sí y de valor q, ocupan los puntos B y D del eje OY, cuyas coordenadas cartesianas son B(0,b,0) y D(0, − b,0). La geometría

del sistema es tal que la distancia que separa dos carta contiguas es

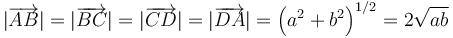
No existen más cargas eléctricas, a parte de las cuatro que constituyen el sistema descrito.

1. ¿Qué relación deben verificar la cantidades de Q y q de las respectivas cargas puntuales descritas en el sistema para que la fuerza eléctrica resultante que actúa sobre la carga que ocupa el punto A sea nula, ?
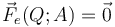2. En las condiciones del apartado anterior, ¿cómo es la fuerza eléctrica resultante que actúa sobre cada una de las otras tres cargas?