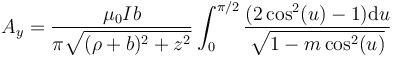Entrar Página Discusión Historial Go to the site toolbox

Campo de un imán anular

De Laplace

(Diferencias entre revisiones)
Línea 33: Línea 33:
y nos queda
y nos queda
-
<center><math>A_y=\frac{\mu_0Ib}{\pi}\int_{0}^{\pi/2} \frac{(2\cos^2(u)-1)\mathrm{d}\theta'}{\sqrt{(\rho+b)^2+z^2-4\rho b\cos^2(u)}}</math></center>
+
<center><math>A_y=\frac{\mu_0Ib}{\pi}\int_{0}^{\pi/2} \frac{(2\cos^2(u)-1)\mathrm{d}u}{\sqrt{(\rho+b)^2+z^2-4\rho b\cos^2(u)}}</math></center>
Nuestro objetivo aquí es llegar a las integrales elípticas completas de primera y segunda especie, E y K
Nuestro objetivo aquí es llegar a las integrales elípticas completas de primera y segunda especie, E y K
Línea 45: Línea 45:
y el potencial vector se expresa
y el potencial vector se expresa
-
<center><math>A_y=\frac{\mu_0Ib}{\pi\sqrt{(\rho+b)^2+z^2}}\int_{0}^{\pi/2} \frac{(2\cos^2(u)-1)\mathrm{d}\theta'}{1-m\cos^2(u)}}</math></center>
+
<center><math>A_y=\frac{\mu_0Ib}{\pi\sqrt{(\rho+b)^2+z^2}}\int_{0}^{\pi/2} \frac{(2\cos^2(u)-1)\mathrm{d}u}{\sqrt{1-m\cos^2(u)}}</math></center>

Revisión de 14:06 14 abr 2018

Contenido

1 Introducción

2 Corrientes equivalentes

3 El campo de una espira circular

Para obtener el campo magnético de una espira consideramos en primer lugar su potencial vector. Posteriormente, mediante el rotacional, podemos hallar el campo magnético.

De acuerdo con la fórmula de Neuman para una espira

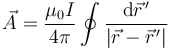
\vec{A}=\frac{\mu_0 I}{4\pi}\oint \frac{\mathrm{d}\vec{r}^{\,\prime}}{|\vec{r}-\vec{r}^{\,\prime}|}

Por la simetría del sistema, tomamos coordenadas cilíndricas. Sin pérdida de generalidad, podemos suponer que el punto \vec{r} se halla sobre el plano OXZ de manera que

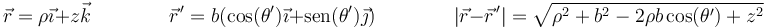
\vec{r}=\rho\vec{\imath}+z\vec{k}\qquad\qquad \vec{r}^{\,\prime}=b(\cos(\theta')\vec{\imath}+\mathrm{sen}(\theta')\vec{\jmath})\qquad\qquad |\vec{r}-\vec{r}^{\,\prime}|=\sqrt{\rho^2+b^2-2\rho b\cos(\theta')+z^2}

siendo el diferencial de camino

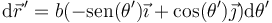
\mathrm{d}\vec{r}^{\,\prime}=b(-\mathrm{sen}(\theta')\vec{\imath}+\cos(\theta')\vec{\jmath})\mathrm{d}\theta'

llevamos esto a la fórmula del potencial vector y queda

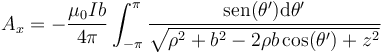
A_x=-\frac{\mu_0Ib}{4\pi}\int_{-\pi}^\pi \frac{\mathrm{sen}(\theta')\mathrm{d}\theta'}{\sqrt{\rho^2+b^2-2\rho b\cos(\theta')+z^2}}

y

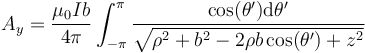
A_y=\frac{\mu_0Ib}{4\pi}\int_{-\pi}^\pi \frac{\cos(\theta')\mathrm{d}\theta'}{\sqrt{\rho^2+b^2-2\rho b\cos(\theta')+z^2}}

La primera de las dos integrales se anula, por tratarse de la integral de una función impar sobre un intervalo par. Para la segunda, aprovechando la simetría, podemos reducirla a

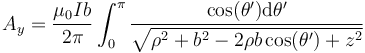
A_y=\frac{\mu_0Ib}{2\pi}\int_{0}^\pi \frac{\cos(\theta')\mathrm{d}\theta'}{\sqrt{\rho^2+b^2-2\rho b\cos(\theta')+z^2}}

Introducimos aquí el ángulo mitad

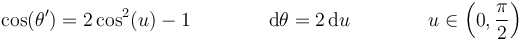
\cos(\theta')=2\cos^2(u)-1\qquad\qquad \mathrm{d}\theta=2\,\mathrm{d}u\qquad\qquad u\in\left(0,\frac{\pi}{2}\right)

y nos queda

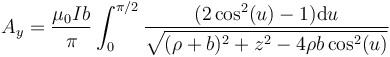
A_y=\frac{\mu_0Ib}{\pi}\int_{0}^{\pi/2} \frac{(2\cos^2(u)-1)\mathrm{d}u}{\sqrt{(\rho+b)^2+z^2-4\rho b\cos^2(u)}}

Nuestro objetivo aquí es llegar a las integrales elípticas completas de primera y segunda especie, E y K

E(m)=\int_0^{\pi/2}\sqrt{1-m\cos^2(u)}\,\mathrm{d}u\qquad\qquad K(m)=\int_0^{\pi/2}\frac{1}{\sqrt{1-m\cos^2(u)}}\,\mathrm{d}u

Definimos

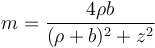
m = \frac{4\rho b}{(\rho+b)^2+z^2}

y el potencial vector se expresa

A_y=\frac{\mu_0Ib}{\pi\sqrt{(\rho+b)^2+z^2}}\int_{0}^{\pi/2} \frac{(2\cos^2(u)-1)\mathrm{d}u}{\sqrt{1-m\cos^2(u)}}


4 El campo de dos espiras concéntricas

5 El campo de un imán anular

6 Imán que cae alrededor de un tubo

Obtenido de "http://tesla.us.es/wiki/index.php/Campo_de_un_im%C3%A1n_anular"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Aviso legal - Acerca de Laplace