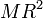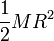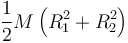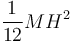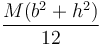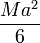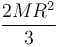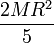Tensor de inercia (M.R.)
De Laplace
(Página creada con '= Introducción = El tensor de inercia de un sólido rígido caracteriza la relación entre el momento cinético del sólido respecto a un punto y su vector rotación. Su cará…') |
|||
| Línea 3: | Línea 3: | ||
El tensor de inercia de un sólido rígido caracteriza la relación entre el momento cinético del sólido respecto a un punto y su vector rotación. Su carácter tensorial se debe a que tanto el momento cinético como el vector rotación son magnitudes vectoriales. | El tensor de inercia de un sólido rígido caracteriza la relación entre el momento cinético del sólido respecto a un punto y su vector rotación. Su carácter tensorial se debe a que tanto el momento cinético como el vector rotación son magnitudes vectoriales. | ||
| - | + | = Momento de inercia respecto a un eje = | |
Para una partícula de masa <math>m</math>, situada en el punto <math>P</math> y con velocidad <math> \vec{v}</math>, su momento cinético respecto a un punto <math>O</math> es | Para una partícula de masa <math>m</math>, situada en el punto <math>P</math> y con velocidad <math> \vec{v}</math>, su momento cinético respecto a un punto <math>O</math> es | ||
| Línea 113: | Línea 113: | ||
</center> | </center> | ||
| - | + | == Ejempos de momentos de inercia respecto a un eje == | |
;Varilla homogénea: Una barra de longitud H con una masa M distribuida uniformemente posee un momento de inercia respecto a un eje perpendicular a ella por su centro | ;Varilla homogénea: Una barra de longitud H con una masa M distribuida uniformemente posee un momento de inercia respecto a un eje perpendicular a ella por su centro | ||
| Línea 220: | Línea 220: | ||
Esto permite estudiar de forma general los problemas de objetos rodantes, suponiendo un cierto factor γ general y luego particularizando | Esto permite estudiar de forma general los problemas de objetos rodantes, suponiendo un cierto factor γ general y luego particularizando | ||
| + | |||
| + | |||
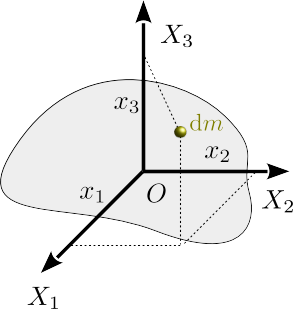
| + | = Momentos de inercia de cuerpos continuos = | ||
| + | [[Archivo:Tensor_de_inercia_03.png|right]] | ||
| + | Se definen momentos de inercia respecto a ejes, planos y puntos. En todos los | ||
| + | casos la definición es similar. Se divide el cuerpo continuo en elementos | ||
| + | diferenciales y el integrando se construye multiplicando la masa del elemento | ||
| + | diferencial por el cuadrado de la distancia el elemento geométrico respecto al | ||
| + | que se define el momento de inercia. | ||
| + | |||
| + | ;Momentos de inercia respecto a los planos coordenados | ||
| + | En cada caso aparece la distancia del elemento de volumen al plano coordenado | ||
| + | correspondiente | ||
| + | <center> | ||
| + | <math> | ||
| + | I_1 = \int\mathrm{d}m \, x_1^2, \qquad | ||
| + | I_2 = \int\mathrm{d}m \, x_2^2, \qquad | ||
| + | I_3 = \int\mathrm{d}m \, x_3^2 | ||
| + | </math> | ||
| + | </center> | ||
| + | También usaremos la notación con <math>XYZ</math> | ||
| + | <center> | ||
| + | <math> | ||
| + | I_x = \int\mathrm{d}m \, x^2 = I_1, \qquad | ||
| + | I_y = \int\mathrm{d}m \, y^2 = I_2, \qquad | ||
| + | I_z = \int\mathrm{d}m \, z^2 = I_3 | ||
| + | </math> | ||
| + | </center> | ||
| + | |||
| + | ;Momentos de inercia respecto a los ejes coordenados | ||
| + | En este caso, en el integrando aparece el cuadrado de la distancia de cada | ||
| + | elemento del sólido al eje coordenado correspondiente | ||
| + | <center> | ||
| + | <math> | ||
| + | \begin{array}{l} | ||
| + | I_{11} = \int\mathrm{d}m \, (x_2^2+x_3^2) = \int\mathrm{d}m\, (y^2+z^2) = I_{xx}, \\ | ||
| + | \\ | ||
| + | I_{22} = \int\mathrm{d}m \, (x_1^2+x_3^2) = \int\mathrm{d}m\, (x^2+z^2) = I_{yy}, \\ | ||
| + | \\ | ||
| + | I_{33} = \int\mathrm{d}m \, (x_1^2+x_2^2) = \int\mathrm{d}m\, (x^2+y^2) = I_{zz}. | ||
| + | \end{array} | ||
| + | </math> | ||
| + | </center> | ||
| + | |||
| + | ;Momentos de inercia respecto a un punto | ||
| + | Ahora aparece en el integrando la distancia de cada punto del sólido al punto en | ||
| + | cuestión. Si el punto es el origen de coordenadas tenemos | ||
| + | <center> | ||
| + | <math> | ||
| + | I_O = \int\mathrm{d}m\, (x_1^2+x_2^2+x_3^2) = \int\mathrm{d}m\,(x^2+y^2+z^2) = | ||
| + | \int\mathrm{d}m\, r^2. | ||
| + | </math> | ||
| + | </center> | ||
| + | |||
| + | ;Relaciones entre los momentos de inercia respecto a elementos cartesianos | ||
| + | Si los elementos geométricos son los planos y ejes cartesianos pueden | ||
| + | demostrarse las siguientes relaciones | ||
| + | <center> | ||
| + | <math> | ||
| + | \begin{array}{l} | ||
| + | I_{11} = I_2 + I_3, \\ | ||
| + | I_{22} = I_1 + I_3, \\ | ||
| + | I_{33} = I_1 + I_3, \\ | ||
| + | I_{O} = (I_{11} + I_{22} + I_{33})/2. | ||
| + | \end{array} | ||
| + | </math> | ||
| + | </center> | ||
| + | Las demostraciones son inmediatas. Por ejemplo, para la primera tenemos | ||
| + | <center> | ||
| + | <math> | ||
| + | I_2 + I_3 = \int\mathrm{d}m\, x_2^2 + \int\mathrm{d}m\, x_3^2 | ||
| + | = | ||
| + | \int\mathrm{d}m\,(x_2^2 + x_3^2) = I_{11}. | ||
| + | </math> | ||
| + | </center> | ||
| + | Las otras se demuestran de manera similar. | ||
| + | |||
| + | Los momentos de | ||
| + | inercia son siempre positivos, pues son sumas de cuadrados. | ||
| + | |||
| + | ;Productos de inercia | ||
| + | En estas magnitudes aparecen mezcladas las distancias de cada punto del sólido a | ||
| + | dos planos coordenados | ||
| + | <center> | ||
| + | <math> | ||
| + | P_{12} = \int\mathrm{d}m \, x_1x_2, \qquad | ||
| + | P_{13} = \int\mathrm{d}m \, x_1x_3, \qquad | ||
| + | P_{23} = \int\mathrm{d}m \, x_2x_3. | ||
| + | </math> | ||
| + | </center> | ||
| + | Los productos de inercia pueden ser negativos o positivos. En la notación | ||
| + | <math>XYZ</math> se escribe | ||
| + | <center> | ||
| + | <math> | ||
| + | P_{xy} = \int\mathrm{d}m \, xy, \qquad | ||
| + | P_{xz} = \int\mathrm{d}m \, xz, \qquad | ||
| + | P_{yz} = \int\mathrm{d}m \, yz. | ||
| + | </math> | ||
| + | </center> | ||
| + | De las definiciones vemos que se cumple | ||
| + | <center> | ||
| + | <math> | ||
| + | P_{ij} = P_{ji}. | ||
| + | </math> | ||
| + | </center> | ||
| + | |||
| + | = Tensor de Inercia = | ||
| + | El Tensor de Inercia de un sólido calculado en el origen de un sistema | ||
| + | cartesiano de coordenadas es un tensor de orden 2 que puede representarse por la | ||
| + | matriz | ||
| + | <center> | ||
| + | <math> | ||
| + | \overset{\leftrightarrow}{I}_O | ||
| + | = | ||
| + | \left[ | ||
| + | \begin{array}{ccc} | ||
| + | I_{11} & -P_{12} & -P_{13}\\ | ||
| + | -P_{21} & I_{22} & -P_{23}\\ | ||
| + | -P_{31} & -P_{21} & I_{33} | ||
| + | \end{array} | ||
| + | \right] | ||
| + | = | ||
| + | \left[ | ||
| + | \begin{array}{ccc} | ||
| + | I_{xx} & -P_{xy} & -P_{xz}\\ | ||
| + | -P_{yx} & I_{yy} & -P_{yz}\\ | ||
| + | -P_{zx} & -P_{zy} & I_{zz} | ||
| + | \end{array} | ||
| + | \right] | ||
| + | </math> | ||
| + | </center> | ||
| + | También recibe el nombre de Matriz de Inercia. Es una matriz simétrica, por las | ||
| + | relaciones que vimos antes de los productos de inercia. | ||
| + | |||
| + | Para un sólido dado, el | ||
| + | Tensor de Inercia es diferente en cada punto el espacio. Podemos definir para cada sólido | ||
| + | un campo tensorial, a cada punto del espacio se le asigna un tensor, el Tensor | ||
| + | de Inercia del sólido calculado en ese punto. | ||
| + | |||
| + | Como ocurre con los vectores, un tensor no depende del sistema de coordenadas en | ||
| + | que se exprese. Esto quiere decir que si el tensor de inercia se expresa en dos | ||
| + | sistemas de coordenadas distintos, las matrices que lo representan serán | ||
| + | diferentes, pero el tensor en sí no cambia. | ||
| + | |||
| + | El Tensor de Inercia puede expresarse también en formato de índices | ||
| + | <center> | ||
| + | <math> | ||
| + | I_{ij} = \int\mathrm{d}\,(r^2\delta_{ij} - x_ix_j), | ||
| + | \qquad\qquad | ||
| + | i,j = 1,2,3. | ||
| + | </math> | ||
| + | </center> | ||
| + | Siendo <math>r^2=x_1^2+x_2^2 + x_3^2</math> y <math>\delta_{ij}</math> es la | ||
| + | [https://es.wikipedia.org/wiki/Delta_de_Kronecker Delta de Kronecker] | ||
Revisión de 16:07 10 abr 2018
Contenido |
1 Introducción
El tensor de inercia de un sólido rígido caracteriza la relación entre el momento cinético del sólido respecto a un punto y su vector rotación. Su carácter tensorial se debe a que tanto el momento cinético como el vector rotación son magnitudes vectoriales.
2 Momento de inercia respecto a un eje
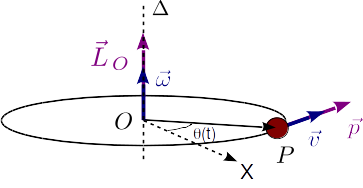
Para una partícula de masa m, situada en el punto P y con velocidad  , su momento cinético respecto a un punto O es
, su momento cinético respecto a un punto O es
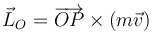
Supongamos una partícula m que describe una circunferencia de radio
R en torno al origen con velocidad angular
 . Su velocidad es
. Su velocidad es
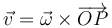
El momento cinético de esta partícula respecto al centro de la circunferencia es perpendicular al plano de ésta y de módulo
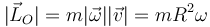
Puesto que en este caso el momento cinético tiene la misma dirección y sentido que la velocidad angular, podemos escribir esta expresión en forma vectorial
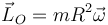
Esta relación entre los vectores rotación y momento cinético es similar a la que
existe entre la velocidad y la cantidad de movimiento, 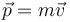 . El escalar que multiplica
al vector rotación, mR2, es una medida de la inercia de la
partícula respecto al movimiento de rotación. Recibe el nombre de momento de inercia de la partícula respecto al eje Δ. El momento de inercia relaciona una magnitud cinemática,
. El escalar que multiplica
al vector rotación, mR2, es una medida de la inercia de la
partícula respecto al movimiento de rotación. Recibe el nombre de momento de inercia de la partícula respecto al eje Δ. El momento de inercia relaciona una magnitud cinemática,  con una magnitud cinética,
con una magnitud cinética,  .
.
IΔ = mR2.
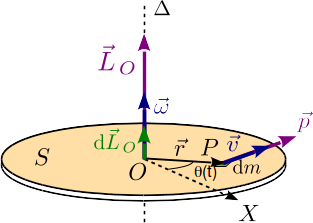
Para un sistema de partículas (por ejemplo, un sólido rígido) el momento
cinético del sistema respecto de un punto es la suma de los momentos cinéticos
de cada una de las partículas que componen el sistema. Supongamos que tenemos un
disco que rota con vector rotación  respecto a un eje
perpendicular a él que pasa por su centro.
respecto a un eje
perpendicular a él que pasa por su centro.
Cada elemento de superficie del disco, de masa dm, realiza un movimiento circular de radio r y con velocidad
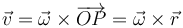
Igual que para la partícula anterior, el momento cinético respecto al centro de disco del elemento de área es
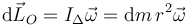
El momento cinético del disco es la suma de los momentos cinéticos de todos los elementos de área que se pueden considerar en el disco. Como es un sistema continuo la suma se convierte en integral
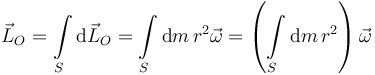
Hemos usado que el vector rotación es el mismo en todos los puntos del sólido (es el invariante vectorial), y lo sacamos de factor común de la integral. La cantidad entre paréntesis es el momento de inercia del disco respecto al eje Δ
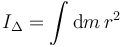
Vemos que en este caso se cumple
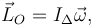
es decir, los vectores momento cinético y rotación son paralelos. En este caso esto ocurre porque el eje de rotación es un eje de simetría del sólido. Si este no es el caso los vectores rotación y momento angular no son paralelos. Un ejemplo sencillo donde el momento cinético no es paralelo a la velocidad angular es el de un rotor desequilibrado.
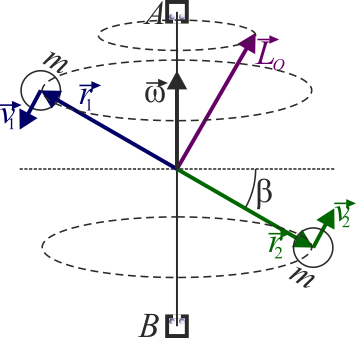
En estos casos todavía existe una relación lineal entre el momento cinético y el
vector rotación. Pero para ello, el momento de inercia respecto a un eje, que es
una magnitud escalar, se ve sustituida por el Tensor de Inercia (o Matriz
de Inercia), 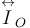 . Esta es una magnitud tensorial, de modo que podemos escribir
. Esta es una magnitud tensorial, de modo que podemos escribir
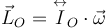
2.1 Ejempos de momentos de inercia respecto a un eje
- Varilla homogénea
- Una barra de longitud H con una masa M distribuida uniformemente posee un momento de inercia respecto a un eje perpendicular a ella por su centro
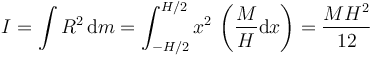
- donde hemos aplicado que por ser homogénea

- Superficie cilíndrica
- Para una superficie cilíndrica de radio R y altura h, el momento de inercia respecto al eje del cilindro es, simplemente
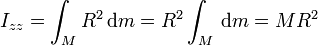
- ya que todos los puntos se encuentran a la misma distancia del eje.
- Cilindro macizo
- Si en cambio consideramos un cilindro macizo homogéneo de radio R y altura h, su momento de inercia es igual a
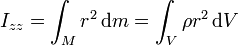
- Como elementos de volumen consideramos finas películas cilíndricas de radio r y espesor dr, cada una de las cuales tiene el volumen diferencial
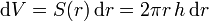
- Llevando esto al momento de inercia nos queda
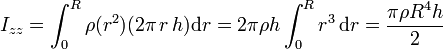
- Vemos que para cilindros del mismo material (con la misma densidad de masa), el momento de inercia va como la cuarta potencia del radio (esto es, doble de radio significa que el momento de inercia se multiplica por 16). Sustituyendo el valor de la densidad de masa
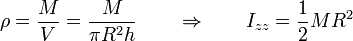
- El momento de inercia de un cilindro macizo es entonces la mitad del de una superficie cilíndrica de la misma masa y el mismo radio.
- Puesto que estos resultados no dependen de la altura del cilindro también son aplicables al caso de un anillo (superficie cilíndrica de altura muy pequeña) y de un disco (cilindro macizo de muy pequeño espesor).
Por su interés, es conveniente tabular casos particulares de momentos de inercia de sólidos homogéneos. Muchos otros pueden hallarse
Vemos que para aquellos que se caracterizan por una sola distancia R (radio, longitud,...), la forma del momento de inercia es
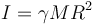
con γ un número que depende del objeto. En particular, para objetos redondos (con R el radio) tenemos
| Cuerpo | Cilindro hueco | Cilindro macizo | Esfera hueca | Esfera maciza |
|---|---|---|---|---|
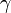
| 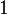
| 
| 
| 
|
Esto permite estudiar de forma general los problemas de objetos rodantes, suponiendo un cierto factor γ general y luego particularizando
3 Momentos de inercia de cuerpos continuos
Se definen momentos de inercia respecto a ejes, planos y puntos. En todos los casos la definición es similar. Se divide el cuerpo continuo en elementos diferenciales y el integrando se construye multiplicando la masa del elemento diferencial por el cuadrado de la distancia el elemento geométrico respecto al que se define el momento de inercia.
- Momentos de inercia respecto a los planos coordenados
En cada caso aparece la distancia del elemento de volumen al plano coordenado correspondiente
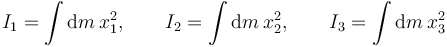
También usaremos la notación con XYZ
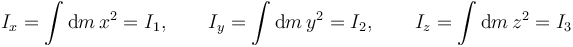
- Momentos de inercia respecto a los ejes coordenados
En este caso, en el integrando aparece el cuadrado de la distancia de cada elemento del sólido al eje coordenado correspondiente
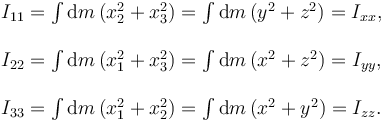
- Momentos de inercia respecto a un punto
Ahora aparece en el integrando la distancia de cada punto del sólido al punto en cuestión. Si el punto es el origen de coordenadas tenemos
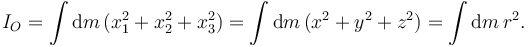
- Relaciones entre los momentos de inercia respecto a elementos cartesianos
Si los elementos geométricos son los planos y ejes cartesianos pueden demostrarse las siguientes relaciones
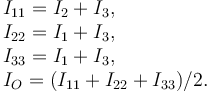
Las demostraciones son inmediatas. Por ejemplo, para la primera tenemos
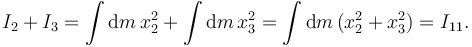
Las otras se demuestran de manera similar.
Los momentos de inercia son siempre positivos, pues son sumas de cuadrados.
- Productos de inercia
En estas magnitudes aparecen mezcladas las distancias de cada punto del sólido a dos planos coordenados
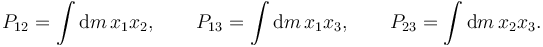
Los productos de inercia pueden ser negativos o positivos. En la notación XYZ se escribe
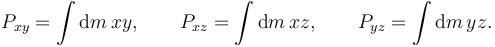
De las definiciones vemos que se cumple
Pij = Pji.
4 Tensor de Inercia
El Tensor de Inercia de un sólido calculado en el origen de un sistema cartesiano de coordenadas es un tensor de orden 2 que puede representarse por la matriz
![\overset{\leftrightarrow}{I}_O
=
\left[
\begin{array}{ccc}
I_{11} & -P_{12} & -P_{13}\\
-P_{21} & I_{22} & -P_{23}\\
-P_{31} & -P_{21} & I_{33}
\end{array}
\right]
=
\left[
\begin{array}{ccc}
I_{xx} & -P_{xy} & -P_{xz}\\
-P_{yx} & I_{yy} & -P_{yz}\\
-P_{zx} & -P_{zy} & I_{zz}
\end{array}
\right]](/wiki/images/math/d/3/6/d36e9713460078815f1644a204d5d347.png)
También recibe el nombre de Matriz de Inercia. Es una matriz simétrica, por las relaciones que vimos antes de los productos de inercia.
Para un sólido dado, el Tensor de Inercia es diferente en cada punto el espacio. Podemos definir para cada sólido un campo tensorial, a cada punto del espacio se le asigna un tensor, el Tensor de Inercia del sólido calculado en ese punto.
Como ocurre con los vectores, un tensor no depende del sistema de coordenadas en que se exprese. Esto quiere decir que si el tensor de inercia se expresa en dos sistemas de coordenadas distintos, las matrices que lo representan serán diferentes, pero el tensor en sí no cambia.
El Tensor de Inercia puede expresarse también en formato de índices
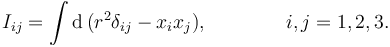
Siendo 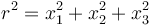 y δij es la
Delta de Kronecker
y δij es la
Delta de Kronecker