Carga distribuida en un anillo (GIE)
De Laplace
(Diferencias entre revisiones)
(Página creada con '==Enunciado== Un anillo de radio R se encuentra en el plano OXY con centro el origen de coordenadas. El anillo almacena una distribución de carga con densidad lineal <center><…') |
|||
| Línea 8: | Línea 8: | ||
# El potencial eléctrico en el origen de coordenadas | # El potencial eléctrico en el origen de coordenadas | ||
# El campo eléctrico en el origen de coordenadas. | # El campo eléctrico en el origen de coordenadas. | ||
| + | |||
| + | ==Carga total== | ||
| + | La carga total es la suma de la de todos los elementos que forman el anillo | ||
| + | |||
| + | <center><math>Q=\int_Q \mathrm{d}q=\int \lambdaº,\mathrm{d}\ell'=\int_{-\pi}^\pi \lambda_0\cos^2\left(\frac{\theta'}{2}\right)\,R\,\mathrm{d}\theta'</math></center> | ||
| + | |||
| + | El resultado de esta integral es | ||
| + | |||
| + | <center><math>Q=\lambda_0 R\int_{-\pi}^{\pi}\cos^2\left(\frac{\theta'}{2}\right)\mathrm{d}\theta'=\frac{\lambda_0 R}{2}\int_{-\pi}^\pi (1-\cos(\theta'))\mathrm{d}\theta'=\lambda_0\pi R</math></center> | ||
| + | ==Potencial en el centro== | ||
| + | Para el potencial en un punto del espacio, la expresión general es | ||
| + | |||
| + | <center><math>V(\vec{r})=\frac{1}{4\pi\varepsilon_0}\int \frac{\mathrm{d}q'}{|\vec{r}-\vec{r}'|}</math></center> | ||
| + | |||
| + | En este caso <math>\vec{r}=\vec{0}</math> ya que queremos el potencial en el centro del anillo. Por tanto | ||
| + | |||
| + | <center><math>|\vec{r}-\vec{r}'|=|\vec{r}'| = R</math></center> | ||
| + | |||
| + | para todos los puntos del anillo. Por ello | ||
| + | |||
| + | <center><math>V(\vec{0})=\frac{1}{4\pi\varepsilon_0}\int \frac{\mathrm{d}q'}{R}=\frac{1}{4\\pi\varepsilon_0R}\int \mathrm{d}q'=\frac{Q}{4\pi\varepsilon_0 R}=\frac{\lambda_0}{4\varepsilon_0}</math></center> | ||
| + | ==Campo en el centro== | ||
Revisión de 16:43 9 abr 2018
Contenido |
1 Enunciado
Un anillo de radio R se encuentra en el plano OXY con centro el origen de coordenadas. El anillo almacena una distribución de carga con densidad lineal
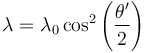
siendo θ' el ángulo que forma con el eje OX el vector de posición de los puntos del anillo. Para esta distribución, halle
- La carga total almacenada
- El potencial eléctrico en el origen de coordenadas
- El campo eléctrico en el origen de coordenadas.
2 Carga total
La carga total es la suma de la de todos los elementos que forman el anillo
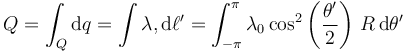
El resultado de esta integral es
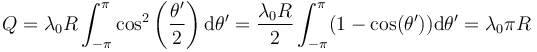
3 Potencial en el centro
Para el potencial en un punto del espacio, la expresión general es
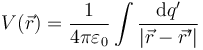
En este caso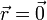 
ya que queremos el potencial en el centro del anillo. Por tanto
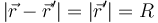
para todos los puntos del anillo. Por ello
