Problemas de Dinámica Impulsiva (MR G.I.C.)
De Laplace
(Diferencias entre revisiones)
(→Barra oscilante sometida a una percusión horizontal) |
(→Barra oscilante sometida a una percusión horizontal) |
||
| Línea 1: | Línea 1: | ||
| + | = Problemas del boletín = | ||
==[[Barra oscilante sometida a una percusión horizontal]]== | ==[[Barra oscilante sometida a una percusión horizontal]]== | ||
[[Imagen:Percusiones_barra_enunciado.jpg|right]] | [[Imagen:Percusiones_barra_enunciado.jpg|right]] | ||
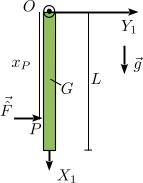
Una barra homogénea de longitud <math>L</math> está articulada en un punto fijo <math>O</math> de modo que puede colgar libremente, sometida a la acción de la gravedad. En el instante inicial se encuentra en reposo y colgando verticalmente. Se aplica un percusión horizontal hacia la derecha a una distancia <math>x_P</math> del punto <math>O</math>. Determina la velocidad angular de la barra justo después de la percusión y las percusiones vinculares. Hazlo usando las herramientas de la Dinámica Vectorial y la Analítica. | Una barra homogénea de longitud <math>L</math> está articulada en un punto fijo <math>O</math> de modo que puede colgar libremente, sometida a la acción de la gravedad. En el instante inicial se encuentra en reposo y colgando verticalmente. Se aplica un percusión horizontal hacia la derecha a una distancia <math>x_P</math> del punto <math>O</math>. Determina la velocidad angular de la barra justo después de la percusión y las percusiones vinculares. Hazlo usando las herramientas de la Dinámica Vectorial y la Analítica. | ||
| + | |||
| + | = Otros problemas = | ||
| + | ==[[ Disco rodando sobre plataforma con muelle (Ene 2018 MR) | Disco rodando sobre plataforma con muelle ]]== | ||
| + | [[Imagen:MR_disco_placa_muelle_enunciado.png|right]] | ||
| + | Un disco de masa <math>m</math> y radio <math>R</math> (sólido "2") rueda sin deslizar sobre una placa | ||
| + | rectangular de masa <math>m</math> (sólido "0"). La placa desliza sin rozamiento sobre el eje fijo | ||
| + | <math>O_1X_1</math>. Un muelle de constante elástica <math>k</math> y longitud natural nula conecta la placa con | ||
| + | el eje <math>O_1Y_1</math>. | ||
| + | #Encuentra la reducción cinemática del movimiento absoluto. | ||
| + | #Escribe la Lagrangiana del sistema. | ||
| + | #Escribe las ecuaciones de Lagrange. | ||
| + | #En el estado inicial los dos sólidos están en reposo y <math>x_0(0)=0</math>, <math>x_2(0)=L/2</math>. Se somete la placa a una percusión <math>\vec{\hat{F}} = \hat{F}_0\,\vec{\imath}_1</math> aplicada en su extremo izquierdo. ¿Cuánto valen las velocidades generalizadas inmediatamente después de la percusión? ¿Cuál es la frecuencia de las oscilaciones de la placa en el movimiento después de la percusión? | ||
última version al 18:55 3 abr 2018
Contenido |
1 Problemas del boletín
1.1 Barra oscilante sometida a una percusión horizontal
Una barra homogénea de longitud L está articulada en un punto fijo O de modo que puede colgar libremente, sometida a la acción de la gravedad. En el instante inicial se encuentra en reposo y colgando verticalmente. Se aplica un percusión horizontal hacia la derecha a una distancia xP del punto O. Determina la velocidad angular de la barra justo después de la percusión y las percusiones vinculares. Hazlo usando las herramientas de la Dinámica Vectorial y la Analítica.
2 Otros problemas
2.1 Disco rodando sobre plataforma con muelle
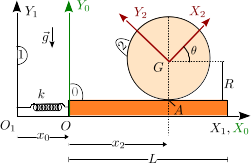
Un disco de masa m y radio R (sólido "2") rueda sin deslizar sobre una placa rectangular de masa m (sólido "0"). La placa desliza sin rozamiento sobre el eje fijo O1X1. Un muelle de constante elástica k y longitud natural nula conecta la placa con el eje O1Y1.
- Encuentra la reducción cinemática del movimiento absoluto.
- Escribe la Lagrangiana del sistema.
- Escribe las ecuaciones de Lagrange.
- En el estado inicial los dos sólidos están en reposo y x0(0) = 0, x2(0) = L / 2. Se somete la placa a una percusión
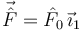aplicada en su extremo izquierdo. ¿Cuánto valen las velocidades generalizadas inmediatamente después de la percusión? ¿Cuál es la frecuencia de las oscilaciones de la placa en el movimiento después de la percusión?
