Problemas de Movimiento ondulatorio
De Laplace
(Diferencias entre revisiones)
(→Solución de onda estacionaria) |
(→Solución de onda estacionaria) |
||
| Línea 22: | Línea 22: | ||
Una perturbación de una cuerda es de la forma | Una perturbación de una cuerda es de la forma | ||
| - | <center><math>y =0.2\cos(126t)\ | + | <center><math>y =0.2\cos(126t)\,\mathrm{sen}\,(0.314x)</math></center> |
con ''x'' e ''y'' medidos en centímetros y ''t'' en segundos. Demuestre que esta función verifica la ecuación de ondas. ¿Qué velocidad le | con ''x'' e ''y'' medidos en centímetros y ''t'' en segundos. Demuestre que esta función verifica la ecuación de ondas. ¿Qué velocidad le | ||
Revisión de 18:45 19 feb 2009
1 Pulso en una cuerda
Los puntos de una cuerda horizontal se mueven verticalmente, de forma que el perfil de la cuerda tiene la forma
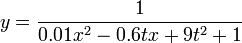
donde x e y se miden en centímetros y t en segundos.
- Halle la velocidad de esta onda.
- Demuestre que esta señal cumple la ecuación de onda.
- Calcule la velocidad del punto de la cuerda situado en x = 15 cm, en (a) t = 0 s, (b) t = 0.5 s, (c) t = 1 s.
2 Propiedades de una onda sinusoidal
Una perturbación a lo largo de una cuerda se describe mediante la ecuación
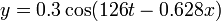
con x e y medidos en centímetros y t en segundos.
Para esta onda, halle su amplitud, frecuencia angular, periodo, número de onda y longitud de onda.
3 Solución de onda estacionaria
Una perturbación de una cuerda es de la forma
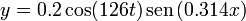
con x e y medidos en centímetros y t en segundos. Demuestre que esta función verifica la ecuación de ondas. ¿Qué velocidad le corresponde?





