Barra apoyada en bloque
De Laplace
(Diferencias entre revisiones)
(Página creada con '==Enunciado== Una barra homogénea de 10 N de peso y 150 cm de longitud está articulada por uno de sus extremos, O. La barra está apoyada sin rozamiento sobre un…') |
(→Enunciado) |
||
| Línea 1: | Línea 1: | ||
==Enunciado== | ==Enunciado== | ||
| - | Una barra homogénea de 10 N de peso y 150 cm de longitud está articulada por uno de sus extremos, O. La barra está apoyada sin rozamiento sobre un bloque cuadrado homogéneo de <math>h=60 cm</math> de lado y 9.6 N de peso fijado al suelo, de manera que su borde está a <math>b=80 | + | Una barra homogénea de 10 N de peso y 150 cm de longitud está articulada por uno de sus extremos, O. La barra está apoyada sin rozamiento sobre un bloque cuadrado homogéneo de <math>h=60 cm</math> de lado y 9.6 N de peso fijado al suelo, de manera que su borde está a <math>b=80\,cm</math> de O. Sea A el punto del bloque donde se apoya la barra. |
# Determine la fuerza que se ejerce sobre la barra en O y en A. | # Determine la fuerza que se ejerce sobre la barra en O y en A. | ||
| Línea 9: | Línea 9: | ||
<li>Halle el momento resultante de las fuerzas de reacción del suelo sobre el bloque respecto a la esquina B de éste.</li> | <li>Halle el momento resultante de las fuerzas de reacción del suelo sobre el bloque respecto a la esquina B de éste.</li> | ||
</ol> | </ol> | ||
| + | |||
==Fuerzas sobre la barra== | ==Fuerzas sobre la barra== | ||
==Fuerza sobre el bloque== | ==Fuerza sobre el bloque== | ||
Revisión de 00:06 1 feb 2018
Contenido |
1 Enunciado
Una barra homogénea de 10 N de peso y 150 cm de longitud está articulada por uno de sus extremos, O. La barra está apoyada sin rozamiento sobre un bloque cuadrado homogéneo de h = 60cm de lado y 9.6 N de peso fijado al suelo, de manera que su borde está a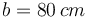 
de O. Sea A el punto del bloque donde se apoya la barra.
- Determine la fuerza que se ejerce sobre la barra en O y en A.
Suponga ahora que el bloque no está soldado al suelo, sino solo apoyado en él, y es mantenido en su posición por la fuerza de rozamiento estático.
- Calcule la resultante de las fuerzas de reacción que el suelo ejerce sobre el bloque.
- Determine el valor mínimo del coeficiente de rozamiento μ para que el sistema se quede en equilibrio.
- Halle el momento resultante de las fuerzas de reacción del suelo sobre el bloque respecto a la esquina B de éste.
