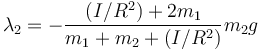Estudio analítico de máquina de Atwood
De Laplace
(Página creada con '==Enunciado== Una máquina de Atwood está formada por dos masas <math>m_1</math> y <math>m_2</math> unidas por un hilo ideal, inextensible y sin masa, que pasa por una polea id…') |
|||
| (5 ediciones intermedias no se muestran.) | |||
| Línea 3: | Línea 3: | ||
# Empleando el principio de D’Alembert halle la aceleración de cada una de las masas. | # Empleando el principio de D’Alembert halle la aceleración de cada una de las masas. | ||
# Con ayuda de los multiplicadores de Lagrange, calcule la tensión del hilo que pasa por la polea. | # Con ayuda de los multiplicadores de Lagrange, calcule la tensión del hilo que pasa por la polea. | ||
| + | #Empleando también multiplicadores, halle la fuerza que ejerce el gancho que sostiene a la polea. | ||
# Suponga ahora que la polea es un disco de radio <math>R</math> con momento de inercia <math>I</math>. ¿Cómo queda en ese caso la aceleración de las masas? ¿Y las tensiones de la cuerda? | # Suponga ahora que la polea es un disco de radio <math>R</math> con momento de inercia <math>I</math>. ¿Cómo queda en ese caso la aceleración de las masas? ¿Y las tensiones de la cuerda? | ||
==Aceleración== | ==Aceleración== | ||
| Línea 48: | Línea 49: | ||
Esta es la tensión de la cuerda que sujeta a ambas masas. | Esta es la tensión de la cuerda que sujeta a ambas masas. | ||
| + | ==Fuerza en el soporte== | ||
| + | Para hallar la fuerza que ejerce el gancho del que cuelga el sistema debemos desvincular esa ligadura, añadiendo el multiplicador de Lagrange correspondiente. | ||
| + | |||
| + | Para ello, añademos una nueva coordenada <math>x_O</math> que representa la posición de la polea. Al introducir esta coordenada cambia el vínculo que habíamos escrito, ya que lo que es constante es la longitud del hilo, lo cual ahora se escribe | ||
| + | |||
| + | <center><math>(x_1-x_O)+(x_2-x_O)=\ell \qquad \Rightarrow\qquad \delta x_1+\delta x_2-2\delta x_O =0</math></center> | ||
| + | |||
| + | Junto a este vínculo, aparece otro, que es el que vamos a desvincular. | ||
| + | |||
| + | <center><math>x_O=0\qquad\Rightarrow\qquad \delta x_O=0</math></center> | ||
| + | |||
| + | Antes de desvincular y teniendo en cuenta que la polea la suponemos sin masa y solo está sometida a fuerzas de reacción vincular, el principio de D'Alembert se escribe | ||
| + | |||
| + | <center><math>m_1(\ddot{x}_1-g)\delta x_1+m_2(\ddot{x}_2-g)\delta x_2 + 0\cdot\delta x_O= 0</math></center> | ||
| + | |||
| + | junto con las dos ecuaciones de vínculo | ||
| + | |||
| + | <center><math>x_1+x_2-2x_O=\ell\qquad\qquad x_O=0</math></center> | ||
| + | |||
| + | y las correspondientes relaciones entre diferenciales | ||
| + | |||
| + | <center><math>\delta x_1+\delta x_2-2\delta x_O=0\qquad\qquad \delta x_O=0</math></center> | ||
| + | |||
| + | Es evidente que sustituyendo las condiciones para <math>x_O</math> recuperamos la solución anterior. | ||
| + | |||
| + | Procedemos a desvincular. Suponemos que no existe el vínculo <math>x_O=0</math> (pero sí se mantiene el otro) y en su lugar aparece una fuerza de reacción de manera que ahora el principio de D'Alembert se escribe | ||
| + | |||
| + | <center><math>m_1(\ddot{x}_1-g)\delta x_1+m_2(\ddot{x}_2-g)\delta x_2 + (-\lambda_O)\delta x_O= 0</math></center> | ||
| + | |||
| + | Sustituimos aquí la relación entre desplazamientos virtuales | ||
| + | |||
| + | <center><math>\delta x_O = \frac{\delta x_1+\delta x_2}{2}</math></center> | ||
| + | |||
| + | y nos queda | ||
| + | |||
| + | <center><math>\left(m_1(\ddot{x}_1-g)-\frac{\lambda_O}{2}\right)\delta x_1+\left(m_2(\ddot{x}_2-g)-\frac{\lambda_O}{2}\right)\delta x_2= 0</math></center> | ||
| + | |||
| + | Al haber quitado el vínculo, estos dos desplazamientos virtuales son independientes, por lo que cada coeficiente debe anularse por separado | ||
| + | |||
| + | <center><math>m_1(\ddot{x}_1-g)-\frac{\lambda_O}{2}=0\qquad\qquad m_2(\ddot{x}_2-g)-\frac{\lambda_O}{2}= 0</math></center> | ||
| + | |||
| + | de donde | ||
| + | |||
| + | <center><math>\lambda_O=2m_1(\ddot{x}_1-g)=-\frac{4m_1m_2}{m_1+m_2}g</math></center> | ||
| + | |||
| + | Esta sería la fuerza que sujeta la polea en su sitio. | ||
| + | |||
==Polea con inercia== | ==Polea con inercia== | ||
| + | ===Aceleración=== | ||
| + | Consideramos ahora el caso de que la polea no sea ideal, sino que tenga un cierto momento de inercia que requiere un trabajo para hacerla girar, arrastrada por la cuerda. Esto nos obliga a añadir un término de rotación al principio de D'Alembert | ||
| + | |||
| + | <center><math>m_1(\ddot{x}_1-g)\delta x_1+m_2(\ddot{x}_2-g)\delta x_2 +I\ddot{\theta}\delta\theta= 0</math></center> | ||
| + | |||
| + | Este ángulo no es independiente de las posiciones de las masas, ya que la polea gira arrastrada por la cuerda. Por ello, además del vínculo | ||
| + | |||
| + | <center><math>x_1+x_2 = \ell \qquad\Rightarrow\qquad \delta x_1 + \delta x_2 = 0</math></center> | ||
| + | |||
| + | tenemos que añadir el | ||
| + | |||
| + | <center><math>\dot{x}_1=R\dot{\theta}\qquad\Rightarrow\qquad \delta x_1-R\,\delta\theta = 0</math></center> | ||
| + | |||
| + | Llevando esto al principio de D'Alembert nos queda | ||
| + | |||
| + | <center><math>m_1(\ddot{x}_1-g)\delta x_1+m_2(-\ddot{x}_1-g)(-\delta x_1) +\left(I\frac{\ddot{x}_1}{R}\right)\left(\frac{\delta x_1}{R}\right)= 0</math></center> | ||
| + | |||
| + | como <math>x_1</math> es libre, debe anularse el coeficiente del desplazamiento, lo que nos da | ||
| + | |||
| + | <center><math>\left(m_1+m_2+\frac{I}{R^2}\right)\ddot{x}_1-(m_1-m_2)g=0</math></center> | ||
| + | |||
| + | y llegamos a la aceleración | ||
| + | |||
| + | <center><math>\ddot{x}_1=\frac{m_1-m_2}{m_1+m_2+(I/R^2)}g</math></center> | ||
| + | |||
| + | Vemos que el efecto ha sido aumentar la inercia del sistema. | ||
| + | ===Tensión sobre la masa 2=== | ||
| + | Para hallar la tensión que tira de la masa 2 debemos romper el vínculo que afecta a la coordenada 2, manteniendo el otro. A cambio, hay que meter una fuerza de reacción asociada al vínculo. Esto nos deja con | ||
| + | |||
| + | <center><math>\left(m_1(\ddot{x}_1-g)-\lambda_2\right)\delta x_1+\left(m_2(\ddot{x}_2-g)-\lambda_2\right)\delta x_2 +\left(I\frac{\ddot{x}_1}{R}\right)\left(\frac{\delta x_1}{R}\right)= 0</math></center> | ||
| + | |||
| + | Ahora <math>\delta x_2</math> es independiente de <math>\delta x_1</math> por lo que obtenemos las ecuaciones | ||
| + | |||
| + | <center><math>\left(m_1+\frac{I}{R^2}\right)\ddot{x}_1=m_1g+\lambda_2 \qquad\qquad m_2\ddot{x}_2=m_2g+\lambda_2</math></center> | ||
| + | |||
| + | De cualquiera de ellas | ||
| + | |||
| + | <center><math>\lambda_2=-\frac{(I/R^2) + 2 m_1}{m_1+m_2+(I/R^2)}m_2g</math></center> | ||
| + | |||
| + | [[Categoría:Problemas de mecánica analítica (CMR)]] | ||
última version al 20:33 24 ene 2018
Contenido |
1 Enunciado
Una máquina de Atwood está formada por dos masas m1 y m2 unidas por un hilo ideal, inextensible y sin masa, que pasa por una polea ideal, sin rozamiento y sin masa.
- Empleando el principio de D’Alembert halle la aceleración de cada una de las masas.
- Con ayuda de los multiplicadores de Lagrange, calcule la tensión del hilo que pasa por la polea.
- Empleando también multiplicadores, halle la fuerza que ejerce el gancho que sostiene a la polea.
- Suponga ahora que la polea es un disco de radio R con momento de inercia I. ¿Cómo queda en ese caso la aceleración de las masas? ¿Y las tensiones de la cuerda?
2 Aceleración
Las dos masas m1 y m2 están unidas por un hilo que pasa por una polea ideal (sin masa y sin rozamiento), de forma que ambas cuelgan verticalmente.
Si consideramos el eje X vertical y hacia abajo, la ecuación fundamental de la dinámica puede escribirse como
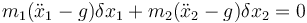
Las coordenadas están relacionadas por el vínculo
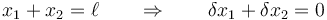
lo que llevado a la ecuación anterior nos da
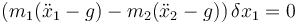
Como δx1 es arbitrario, el coeficiente debe anularse:
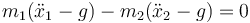
Por otro lado, del mismo vínculo tenemos
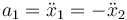
y por tanto
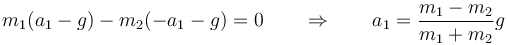
3 Tensión
Si deseamos hallar la tensión del hilo debemos desvincular la relación
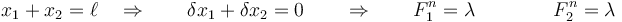
Vemos que la tensión es la misma para las dos masas. Llevamos esto a la ecuación de D'Alembert
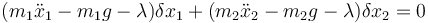
Al desaparecer el vínculo ambos diferenciales son independientes, por lo que los coeficientes deben anularse por separado

Dado que ya conocemos la aceleración, de cualquiera de estas dos ecuaciones podemos hallar el multiplicador de Lagrange (el resultado, lógicamente, debe ser el mismo).
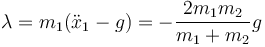
Esta es la tensión de la cuerda que sujeta a ambas masas.
4 Fuerza en el soporte
Para hallar la fuerza que ejerce el gancho del que cuelga el sistema debemos desvincular esa ligadura, añadiendo el multiplicador de Lagrange correspondiente.
Para ello, añademos una nueva coordenada xO que representa la posición de la polea. Al introducir esta coordenada cambia el vínculo que habíamos escrito, ya que lo que es constante es la longitud del hilo, lo cual ahora se escribe
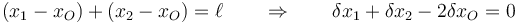
Junto a este vínculo, aparece otro, que es el que vamos a desvincular.
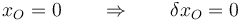
Antes de desvincular y teniendo en cuenta que la polea la suponemos sin masa y solo está sometida a fuerzas de reacción vincular, el principio de D'Alembert se escribe
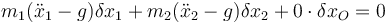
junto con las dos ecuaciones de vínculo
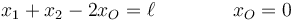
y las correspondientes relaciones entre diferenciales
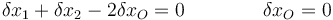
Es evidente que sustituyendo las condiciones para xO recuperamos la solución anterior.
Procedemos a desvincular. Suponemos que no existe el vínculo xO = 0 (pero sí se mantiene el otro) y en su lugar aparece una fuerza de reacción de manera que ahora el principio de D'Alembert se escribe
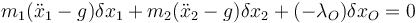
Sustituimos aquí la relación entre desplazamientos virtuales
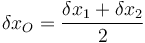
y nos queda
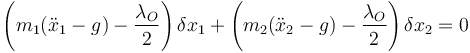
Al haber quitado el vínculo, estos dos desplazamientos virtuales son independientes, por lo que cada coeficiente debe anularse por separado

de donde
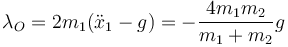
Esta sería la fuerza que sujeta la polea en su sitio.
5 Polea con inercia
5.1 Aceleración
Consideramos ahora el caso de que la polea no sea ideal, sino que tenga un cierto momento de inercia que requiere un trabajo para hacerla girar, arrastrada por la cuerda. Esto nos obliga a añadir un término de rotación al principio de D'Alembert
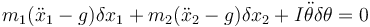
Este ángulo no es independiente de las posiciones de las masas, ya que la polea gira arrastrada por la cuerda. Por ello, además del vínculo
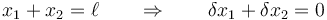
tenemos que añadir el

Llevando esto al principio de D'Alembert nos queda
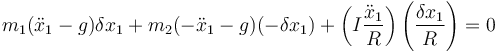
como x1 es libre, debe anularse el coeficiente del desplazamiento, lo que nos da
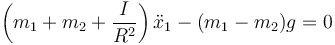
y llegamos a la aceleración
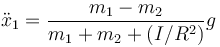
Vemos que el efecto ha sido aumentar la inercia del sistema.
5.2 Tensión sobre la masa 2
Para hallar la tensión que tira de la masa 2 debemos romper el vínculo que afecta a la coordenada 2, manteniendo el otro. A cambio, hay que meter una fuerza de reacción asociada al vínculo. Esto nos deja con
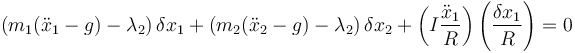
Ahora δx2 es independiente de δx1 por lo que obtenemos las ecuaciones
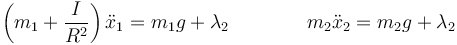
De cualquiera de ellas