Dos barras articuladas (CMR)

De Laplace

(Diferencias entre revisiones)

Revisión de 20:00 12 ene 2018

Contenido

1 Enunciado
2 Lagrangiana del sistema
3 Ecuaciones de movimiento
4 Cambio de coordenadas
5 Nuevas ecuaciones de movimiento
6 Constantes de movimiento
7 Reducción del sistema
8 Lagrangiana con varilla rotatoria
9 Ecuación con varilla rotatoria
10 Magnitud conservada

1 Enunciado

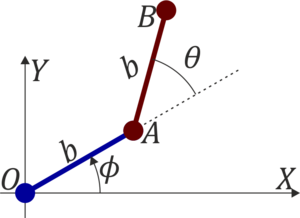
Un sistema está formado por dos varillas homogéneas, ambas de masa $m$ y longitud $b$ , situadas sobre un plano horizontal (“sólido 1”). La varilla “2” está articulada por su extremo O a un punto fijo del plano, mientras que por su extremo A está articulada a la varilla “3”.

Escriba la lagrangiana del sistema, empleando como coordenadas generalizadas los ángulos que ambas varillas forman con el eje $O X 1$ , ϕ (para la varilla 2) y ψ (para la 3).
Obtenga las ecuaciones de movimiento para estos dos ángulos.
¿Es cíclica alguna de estas coordenadas?

Si en lugar de esas coordenadas se usan el ángulo ϕ que la varilla OA forma con OX y el ángulo θ que AB forma con la prolongación de OA

¿Cómo queda la lagrangiana?
¿Y las ecuaciones de movimiento para estos ángulos?
¿Es cíclica alguna de estas coordenadas?
Determine dos constantes de movimiento para este sistema.
Con ayuda de estas constantes, reduzca el problema a una única ecuación de movimiento para el ángulo θ.

Suponga ahora que la varilla 2 es forzada a girar con velocidad angular constante Ω en torno a O.

Escriba la lagrangiana para este sistema en función del ángulo θ.
Obtenga la ecuación de movimiento para θ. ¿Es la misma que en el apartado (8)?
¿Se conserva la energía en este sistema? ¿Hay alguna otra constante de movimiento?

2 Lagrangiana del sistema

La lagrangiana del sistema se calcula como

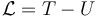
$\mathcal{L}=T-U$

siendo $T = K$ la energía cinética y U la potencial. En este caso, que no hay ninguna fuerza externa conservativa actuando sobre las varillas, esta energía potencial es nula.

$U=0\,$

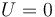
La energía cinética es la suma de las de las dos varillas

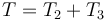
$T=T_2+T_3\,$

La de la varilla 2 se calcula como la de una barra que gira en torno a un eje perpendicular por su extremo

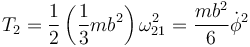
$T_2=\frac{1}{2}\left(\frac{1}{3}mb^2\right)\omega_{21}^2=\frac{mb^2}{6}\dot{\phi}^2$

Para la varilla 3 aplicamos el teorema de König

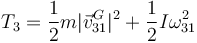
$T_3=\frac{1}{2}m|\vec{v}^{G}_{31}|^2+\frac{1}{2}I\omega_{31}^2$

siendo G el centro de masas de la varilla 3.

No hace falta añadir más términos en la energía cinética de rotación porque el eje OZ es uno principal de inercia para ambas varillas y por tanto el momento cinético es paralelo a la velocidad angular

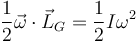
$\frac{1}{2}\vec{\omega}\cdot\vec{L}_G=\frac{1}{2}I\omega^2$

Este término de rotación vale

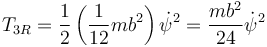
$T_{3R}=\frac{1}{2}\left(\frac{1}{12}mb^2\right)\dot{\psi}^2=\frac{mb^2}{24}\dot{\psi}^2$

La velocidad del centro de la varilla 3 la calculamos mediante la expresión del campo de velocidades de un sólido

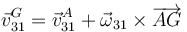
$\vec{v}^G_{31}=\vec{v}^A_{31}+\vec{\omega}_{31}\times\overrightarrow{AG}$

La velocidad de A la calculamos usando que es una articulación

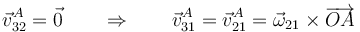
$\vec{v}^A_{32}=\vec{0}\qquad\Rightarrow\qquad \vec{v}^A_{31}=\vec{v}^A_{21}=\vec{\omega}_{21}\times \overrightarrow{OA}$

Sustituimos la posición relativa y la velocidad angular

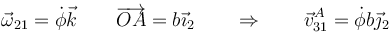
$\vec{\omega}_{21}=\dot{\phi}\vec{k}\qquad\overrightarrow{OA}=b\vec{\imath}_2\qquad\Rightarrow\qquad \vec{v}^A_{31}=\dot{\phi}b\vec{\jmath}_2$

siendo 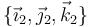$\{\vec{\imath}_2,\vec{\jmath}_2,\vec{k}_2\}$ una base ligada al sólido 2 (aunque por ser un sistema plano 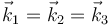$\vec{k}_1=\vec{k}_2=\vec{k}_3$ , por lo que el subíndice es superfluo). Por otro lado,

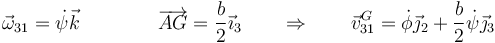
$\vec{\omega}_{31}=\dot{\psi}\vec{k}\qquad\qquad \overrightarrow{AG}=\frac{b}{2}\vec{\imath}_3\qquad\Rightarrow\qquad \vec{v}^G_{31}=\dot{\phi}\vec{\jmath}_{2}+\frac{b}{2}\dot{\psi}\vec{\jmath}_3$

Obsérvese que la expresión contiene vectores de dos bases diferentes, por lo que hay que ser cuidadoso a la hora de hallar la energía cinética de traslación

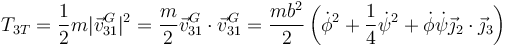
$T_{3T}=\frac{1}{2}m|\vec{v}^{G}_{31}|^2=\frac{m}{2}\vec{v}^{G}_{31}\cdot\vec{v}^{G}_{31}=\frac{mb^2}{2}\left(\dot{\phi}^2+\frac{1}{4}\dot{\psi}^2+\dot{\phi}\dot{\psi}\vec{\jmath}_2\cdot\vec{\jmath}_3\right)$

El producto escalar de dos vectores unitarios es igual al coseno del ángulo que forman

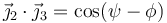
$\vec{\jmath}_2\cdot\vec{\jmath}_3=\cos(\psi-\phi)$

Sumando todos los términos en la energía cinética obtenemos la total, que coincide con la lagrangiana

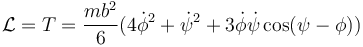
$\mathcal{L}=T=\frac{mb^2}{6}(4\dot{\phi}^2+\dot{\psi}^2+3\dot{\phi}\dot{\psi}\cos(\psi-\phi))$

3 Ecuaciones de movimiento

Estas dos coordenadas son independientes, por lo que podemos emplear las ecuaciones de Lagrange.

3.1 Para la coordenada ϕ

La ecuación para esta coordenada es

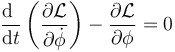
$\frac{\mathrm{d}\ }{\mathrm{d}t}\left(\frac{\partial\mathcal{L}}{\partial\dot{\phi}}\right)-\frac{\partial\mathcal{L}}{\partial\phi}=0$

Calculamos en primer lugar el momento conjugado

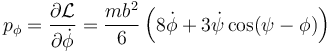
$p_\phi=\frac{\partial\mathcal{L}}{\partial\dot{\phi}}= \frac{mb^2}{6}\left(8\dot{\phi}+3\dot{\psi}\cos(\psi-\phi)\right)$

siendo su derivada temporal

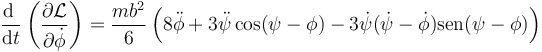
$\frac{\mathrm{d}\ }{\mathrm{d}t}\left(\frac{\partial\mathcal{L}}{\partial\dot{\phi}}\right)=\frac{mb^2}{6}\left(8\ddot{\phi}+3\ddot{\psi}\cos(\psi-\phi)-3\dot{\psi}(\dot{\psi}-\dot{\phi})\mathrm{sen}(\psi-\phi)\right)$

Por otro lado

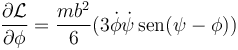
$\frac{\partial\mathcal{L}}{\partial\phi}=\frac{mb^2}{6}(3\dot{\phi}\dot{\psi}\,\mathrm{sen}(\psi-\phi))$

Si sustituimos en la ecuación de Lagrange queda

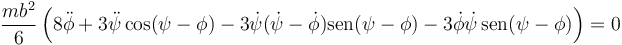
$\frac{mb^2}{6}\left(8\ddot{\phi}+3\ddot{\psi}\cos(\psi-\phi)-3\dot{\psi}(\dot{\psi}-\dot{\phi})\mathrm{sen}(\psi-\phi)-3\dot{\phi}\dot{\psi}\,\mathrm{sen}(\psi-\phi)\right)=0$

que, simplificada, se reduce a

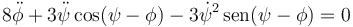
$8\ddot{\phi}+3\ddot{\psi}\cos(\psi-\phi)-3\dot{\psi}^2\,\mathrm{sen}(\psi-\phi)=0$

3.2 Para la coordenada ψ

La ecuación para esta coordenada es

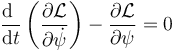
$\frac{\mathrm{d}\ }{\mathrm{d}t}\left(\frac{\partial\mathcal{L}}{\partial\dot{\psi}}\right)-\frac{\partial\mathcal{L}}{\partial\psi}=0$

El momento conjugado de esta coordenada vale

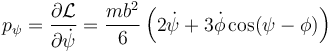
$p_\psi=\frac{\partial\mathcal{L}}{\partial\dot{\psi}}= \frac{mb^2}{6}\left(2\dot{\psi}+3\dot{\phi}\cos(\psi-\phi)\right)$

siendo su derivada temporal

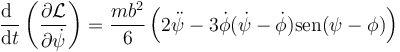
$\frac{\mathrm{d}\ }{\mathrm{d}t}\left(\frac{\partial\mathcal{L}}{\partial\dot{\psi}}\right)=\frac{mb^2}{6}\left(2\ddot{\psi}-3\dot{\phi}(\dot{\psi}-\dot{\phi})\mathrm{sen}(\psi-\phi)\right)$

Por otro lado

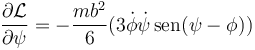
$\frac{\partial\mathcal{L}}{\partial\psi}=-\frac{mb^2}{6}(3\dot{\phi}\dot{\psi}\,\mathrm{sen}(\psi-\phi))$

Sustituimos en la ecuación de Lagrange correspondiente

$\frac{\mathrm{d}\ }{\mathrm{d}t}\left(\frac{\partial\mathcal{L}}{\partial\dot{\psi}}\right)=\frac{mb^2}{6}\left(2\ddot{\psi}-3\dot{\phi}(\dot{\psi}-\dot{\phi})\mathrm{sen}(\psi-\phi)+3\dot{\phi}\dot{\psi}\,\mathrm{sen}(\psi-\phi)\right)=0$

que, simplificada, queda

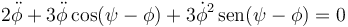
$2\ddot{\phi}+3\ddot{\phi}\cos(\psi-\phi)+3\dot{\phi}^2\,\mathrm{sen}(\psi-\phi)=0$

3.3 Sistema de ecuaciones

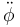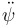Estas dos ecuaciones son acopladas en el sentido de que ambas combinan las dos aceleraciones angulares. Podemos despejar cada una de estas tratando las ecuaciones de Lagrange como un sistema de dos ecuaciones con dos incógnitas ( $\ddot{\phi}$ y $\ddot{\psi}$ ). El resultado es

$\ddot{\phi}=\dfrac{3S \left(3 C \dot{\phi}^2+2\dot{\psi}^2\right)}{16-9 C^2}\qquad\qquad \ddot{\psi}=-\dfrac{3S \left(3 C \dot{\psi}^2+8\dot{\phi}^2\right)}{16-9 C^2}$

siendo

$S=\mathrm{sen}(\psi-\phi)\qquad \qquad C=\cos(\psi-\phi)$

Vemos que el sistema de ecuaciones no es en absoluto trivial. Su solución requiere del uso de software para computar la evolución en el tiempo de estas variables.

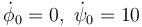
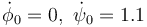
$\dot{\phi}_0=0,\ \dot{\psi}_0=10$	$\dot{\phi}_0=0,\ \dot{\psi}_0=1.1$
Archivo:Dos-varillas-01.png	Archivo:Dos-varillas-02.png
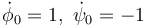
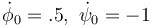
$\dot{\phi}_0=1,\ \dot{\psi}_0=-1$	$\dot{\phi}_0=.5,\ \dot{\psi}_0=-1$
Archivo:Dos-varillas-03.png	Archivo:Dos-varillas-04.png

4 Cambio de coordenadas

5 Nuevas ecuaciones de movimiento

6 Constantes de movimiento

7 Reducción del sistema

8 Lagrangiana con varilla rotatoria

9 Ecuación con varilla rotatoria

10 Magnitud conservada

@@ Línea 134: / Línea 134: @@
 <center><math>
-\ddot{\phi}=\dfrac{3S \left(-3 C \dot{\phi}^2-2\dot{\psi}^2\right)}{9 C^2-16}\qquad\qquad
+\ddot{\phi}=\dfrac{3S \left(3 C \dot{\phi}^2+2\dot{\psi}^2\right)}{16-9 C^2}\qquad\qquad
-\ddot{\psi}=-\dfrac{3S \left(-3 C  \dot{\psi}^2-8\dot{\phi}^2\right)}{9 C^2-16}</math></center>
+\ddot{\psi}=-\dfrac{3S \left(3 C  \dot{\psi}^2+8\dot{\phi}^2\right)}{16-9 C^2}</math></center>
 siendo
@@ Línea 143: / Línea 143: @@
 Vemos que el sistema de ecuaciones no es en absoluto trivial. Su solución requiere del uso de software para computar la evolución en el tiempo de estas variables.
+{| class="bordeado"
+|-
+! <math>\dot{\phi}_0=0,\ \dot{\psi}_0=10</math>
+! <math>\dot{\phi}_0=0,\ \dot{\psi}_0=1.1</math>
+|-
+| [[Archivo:dos-varillas-01.png]]
+| [[Archivo:dos-varillas-02.png]]
+|-
+! <math>\dot{\phi}_0=1,\ \dot{\psi}_0=-1</math>
+! <math>\dot{\phi}_0=.5,\ \dot{\psi}_0=-1</math>
+|-
+| [[Archivo:dos-varillas-03.png]]
+| [[Archivo:dos-varillas-04.png]]
+|}
 ==Cambio de coordenadas==
 ==Nuevas ecuaciones de movimiento==

Dos barras articuladas (CMR)

De Laplace

Revisión de 20:00 12 ene 2018

Contenido

1 Enunciado

2 Lagrangiana del sistema

3 Ecuaciones de movimiento

3.1 Para la coordenada ϕ

3.2 Para la coordenada ψ

3.3 Sistema de ecuaciones

4 Cambio de coordenadas

5 Nuevas ecuaciones de movimiento

6 Constantes de movimiento

7 Reducción del sistema

8 Lagrangiana con varilla rotatoria

9 Ecuación con varilla rotatoria

10 Magnitud conservada

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES