Péndulo compuesto (CMR)
De Laplace
(→Energía mecánica) |
|||
| (3 ediciones intermedias no se muestran.) | |||
| Línea 7: | Línea 7: | ||
## La fuerza que realiza el soporte en O. ¿Cuánto ha aumentado o disminuido respecto a la situación de equilibrio? | ## La fuerza que realiza el soporte en O. ¿Cuánto ha aumentado o disminuido respecto a la situación de equilibrio? | ||
# Suponga que la articulación en O es un par de revolución, de forma que solo puede moverse en el plano OXZ | # Suponga que la articulación en O es un par de revolución, de forma que solo puede moverse en el plano OXZ | ||
| - | ## Obtenga | + | ## Obtenga las ecuacions de movimiento para el ángulo que forma con la vertical |
## Halle las frecuencia de las pequeñas oscilaciones que realiza cuando se suelta desde una posición próxima a la vertical. | ## Halle las frecuencia de las pequeñas oscilaciones que realiza cuando se suelta desde una posición próxima a la vertical. | ||
## Para el caso del enunciado, que se suelta desde la posición horizontal, calcule la fuerza que ejerce el soporte en O para cada ángulo θ | ## Para el caso del enunciado, que se suelta desde la posición horizontal, calcule la fuerza que ejerce el soporte en O para cada ángulo θ | ||
| Línea 258: | Línea 258: | ||
<center><math>\vec{\omega}_{01}=\dot{\phi}\vec{k}_1=\dot{\phi}\vec{k}_0\qquad\qquad\vec{\alpha}_{01}=\ddot{\phi}\vec{k}_1=\ddot{\phi}\vec{k}_0</math></center> | <center><math>\vec{\omega}_{01}=\dot{\phi}\vec{k}_1=\dot{\phi}\vec{k}_0\qquad\qquad\vec{\alpha}_{01}=\ddot{\phi}\vec{k}_1=\ddot{\phi}\vec{k}_0</math></center> | ||
| + | {| class="bordeado" | ||
| + | |- | ||
| + | ! Vista cenital | ||
| + | ! Vista frontal | ||
| + | |- | ||
| + | | [[Archivo:pendulo-compuesto-01.png]] | ||
| + | | [[Archivo:pendulo-compuesto-02.png]] | ||
| + | |} | ||
La relación entre el sistema intermedio y el ligado al sólido la dan las relaciones | La relación entre el sistema intermedio y el ligado al sólido la dan las relaciones | ||
| Línea 269: | Línea 277: | ||
<center><math>\vec{\omega}_{20}=\dot{\theta}\vec{\imath}_0=\dot{\theta}\vec{\imath}_2\qquad\qquad\vec{\alpha}_{20}=\ddot{\theta}\vec{\imath}_0=\ddot{\theta}\vec{\imath}_0</math></center> | <center><math>\vec{\omega}_{20}=\dot{\theta}\vec{\imath}_0=\dot{\theta}\vec{\imath}_2\qquad\qquad\vec{\alpha}_{20}=\ddot{\theta}\vec{\imath}_0=\ddot{\theta}\vec{\imath}_0</math></center> | ||
| + | |||
===Teorema del momento cinético=== | ===Teorema del momento cinético=== | ||
De nuevo, la forma más directa de llegar a las ecuaciones de movimiento es mediante el teorema del momento cinético, empleando como centro de reducción el punto fijo O. Respecto a este punto se cumple | De nuevo, la forma más directa de llegar a las ecuaciones de movimiento es mediante el teorema del momento cinético, empleando como centro de reducción el punto fijo O. Respecto a este punto se cumple | ||
| Línea 276: | Línea 285: | ||
El momento cinético posee una expresión sencilla en el sistema 2, ya que en este los ejes cartesianos son ejes principales. Se cumple | El momento cinético posee una expresión sencilla en el sistema 2, ya que en este los ejes cartesianos son ejes principales. Se cumple | ||
| - | <center><math>I_{XX}=I_{YY}=\frac{1}{ | + | <center><math>I_{XX}=I_{YY}=I_0=\frac{1}{3}mb^2\qquad\qquad I_{ZZ}=0</math></center> |
Por tanto, en este sistema | Por tanto, en este sistema | ||
| Línea 294: | Línea 303: | ||
<center><math>\vec{L}_O=I_0(\dot{\theta}\vec{\imath}_2+\dot{\phi}S\vec{\jmath}_2)</math></center> | <center><math>\vec{L}_O=I_0(\dot{\theta}\vec{\imath}_2+\dot{\phi}S\vec{\jmath}_2)</math></center> | ||
| - | A la hora de derivar esta expresión debemos tener en cuenta que los | + | A la hora de derivar esta expresión debemos tener en cuenta que los vectores de la base dependen del tiempo, por lo que debemos emplear la fórmula de Poisson |
<center><math>\left.\frac{\mathrm{d}\vec{L}_O}{\mathrm{d}t}\right|_1=\left.\frac{\mathrm{d}\vec{L}_O}{\mathrm{d}t}\right|_2+\vec{\omega}_{21}\times\vec{L}_O= | <center><math>\left.\frac{\mathrm{d}\vec{L}_O}{\mathrm{d}t}\right|_1=\left.\frac{\mathrm{d}\vec{L}_O}{\mathrm{d}t}\right|_2+\vec{\omega}_{21}\times\vec{L}_O= | ||
| Línea 302: | Línea 311: | ||
<center><math>\left\{\begin{array}{rcrcl}x:&\quad& I_0\dot{\omega}_X-I_0\omega_Z\omega_Y & = & M_{OX}\\ | <center><math>\left\{\begin{array}{rcrcl}x:&\quad& I_0\dot{\omega}_X-I_0\omega_Z\omega_Y & = & M_{OX}\\ | ||
| - | + | y:&\quad& I_0\dot{\omega}_Y+I_0\omega_Z\omega_X & = & M_{OY}\\z:&\quad&0&=&M_{OZ}\end{array}\right.</math></center> | |
| + | |||
| + | En el segundo miembro aparecen las componentes del momento de las fuerzas (el peso, en este caso), expresadas en la base 2. | ||
| + | |||
| + | La posición del CM en esta base es simplemente | ||
| + | |||
| + | <center><math>\overrightarrow{OG}=-\frac{b}{2}\vec{k}_2</math></center> | ||
| + | |||
| + | mientras que el peso se escribe | ||
| + | |||
| + | <center><math>m\vec{g}=-mg\vec{k}_0=-mg(S\vec{\jmath}_2+C\vec{k}_2)</math></center> | ||
| + | |||
| + | lo que nos da un momento | ||
| + | |||
| + | <center><math>\vec{M}_O=\overrightarrow{OG}\times(m\vec{g})=-\frac{mgb}{2}S\vec{\imath}_2</math></center> | ||
| + | |||
| + | y llegamos a las ecuaciones | ||
| + | |||
| + | <center><math>\left\{\begin{array}{rcrcl}x:&\quad& \dot{\omega}_X-\omega_Z\omega_Y & = & -\dfrac{3g}{2b}S\\ | ||
| + | y:&\quad& \dot{\omega}_Y+\omega_Z\omega_X & = & 0\\z:&\quad&0&=&0\end{array}\right.</math></center> | ||
| + | |||
| + | Si ahora sustituimos las componentes de la velocidad angular y sus derivadas llegamos a | ||
| + | |||
| + | <center><math> \ddot{\theta}-\dot{\phi}^2SC = -\dfrac{3g}{2b}S</math></center> | ||
| + | |||
| + | y | ||
| + | |||
| + | <center><math>\ddot{\phi}S+2\dot{\phi}\dot{\theta}C = 0</math></center> | ||
| + | |||
| + | Estas son las ecuaciones que gobiernan la orientación de la varilla. Son ecuaciones no lineales cuya solución completa requiere el uso de ordenador. | ||
| + | |||
| + | Como caso particular vemos que si la varilla oscila en un plano vertical inmóvil (<math>\dot{\phi}=0</math>) la primera ecuación se reduce a la que ya obtvimos | ||
| + | |||
| + | <center><math>(\dot{\phi}=0)\qquad\qquad \ddot{\theta}-\dot{\phi}^2SC = -\dfrac{3g}{2b}S</math></center> | ||
===Teorema de la cantidad de movimiento=== | ===Teorema de la cantidad de movimiento=== | ||
Como en el caso del movimiento plano, se cumple que | Como en el caso del movimiento plano, se cumple que | ||
| Línea 311: | Línea 353: | ||
<center><math>\vec{F}_O=m\left(\vec{a}_G-\vec{g}\right)</math></center> | <center><math>\vec{F}_O=m\left(\vec{a}_G-\vec{g}\right)</math></center> | ||
| + | |||
| + | ===Constantes de movimiento=== | ||
| + | En este sistema tenemos dos constantes de movimiento no triviales. Las podemos calcular integrando las ecuaciones anteriores o mediante análisis de las magnitudes físicas. Antes empleamos el primer camino, ahora usaremos el segundo. | ||
| + | ====Componente vertical del momento cinético==== | ||
| + | La única fuerza que produce momento respecto del punto O, que tiene una dirección puramente vertical. Esto implica que su momento es puramente horizontal | ||
| + | |||
| + | <center><math>m\vec{g}=-mg\vec{k}_1\qquad\Rightarrow\qquad \vec{M}_O\perp \vec{k}_1</math></center> | ||
| + | |||
| + | y por tanto la componente del momento cinético en dicha dirección es constante | ||
| + | |||
| + | <center><math>L_{0z_1}=\vec{L}_O\cdot\vec{k}_1=\mathrm{cte}.</math></center> | ||
| + | |||
| + | Se trata de expresar ahora este resultado en función de las variables del sistema. Según hemos dicho, el momento cinético tiene la expresión | ||
| + | |||
| + | <center><math>\vec{L}_O=I_0\left(\omega_X\vec{\imath}_2+\omega_Y\vec{\jmath}_2\right)</math></center> | ||
| + | |||
| + | y por tanto, la cantidad que es constante es | ||
| + | |||
| + | <center><math>L_{Oz_1}=I_0\left(\omega_X\vec{\imath}_2\cdot{k}_1+\omega_Y\vec{\jmath}_2\cdot\vec{k}_1\right)</math></center> | ||
| + | |||
| + | Para los productos escalares usamos las relaciones entre las bases que enunciamos antes | ||
| + | |||
| + | <center><math>\vec{\imath}_2\cdot\vec{k}_1=\vec{\imath}_0\cdot\vec{k}_0=0</math></center> | ||
| + | |||
| + | y | ||
| + | |||
| + | <center><math>\vec{\jmath}_2\cdot\vec{k}_1=(C\vec{\jmath}_0+S\vec{k}_0)\cdot\vec{k}_0=S</math></center> | ||
| + | |||
| + | Como además | ||
| + | |||
| + | <center><math>\omega_Y= \dot{\phi}S</math></center> | ||
| + | |||
| + | Llegamos a la constante de movimiento | ||
| + | |||
| + | <center><math>L_{Oz_1}=\frac{1}{3}mb^2\dot{\phi}S^2=\mathrm{cte}</math></center> | ||
| + | |||
| + | Podíamos haber llegado a este resultado integrando la segunda de las ecuaciones de movimiento. | ||
| + | |||
| + | El valor de la constante lo obtenemos de las condiciones iniciales. | ||
| + | |||
| + | <center><math>L_{0z_1}=\frac{1}{3}mb^2\dot{\phi}_0S_0^2\qquad\qquad (S_0=\mathrm{sen}(\theta_0)\ )</math></center> | ||
| + | ====Energía mecánica==== | ||
| + | Este sistema es conservativo, ya que sobre él actúan solo dos fuerzas: | ||
| + | * el peso, que deriva de un potencial, | ||
| + | *la reacción en O, que por actuar sobre un punto de velocidad nula no modifica la energía mecánica del sistema. | ||
| + | Por tanto | ||
| + | |||
| + | <center><math>E=K+U=\mathrm{cte}\,</math></center> | ||
| + | |||
| + | siendo la energía cinética | ||
| + | |||
| + | <center><math>K=T=\frac{1}{2}\vec{\omega}\cdot\bar{\bar{I}}\cdot\vec{\omega}=\frac{I_0}{2}(\omega_X^2+\omega_Y^2)=\frac{mb^2}{6}(\dot{\theta}^2+\dot{\phi}^2S^2)</math></center> | ||
| + | |||
| + | y la potencial | ||
| + | |||
| + | <center><math>U=mgz_G=-mg\frac{b}{2}C</math></center> | ||
| + | |||
| + | lo que nos da la constante | ||
| + | |||
| + | <center><math>E=\frac{mb^2}{6}(\dot{\theta}^2+\dot{\phi}^2S^2)-\frac{mgb}{2}C</math></center> | ||
| + | |||
| + | ===Ecuación de movimiento reducida=== | ||
| + | La conservación de la componente del momento cinético nos permite expresar <math>\dot{\phi}</math> en función del ángulo θ | ||
| + | |||
| + | <center><math>\dot{\phi}=\frac{3L_{Oz_1}}{mb^2S^2}=\frac{\dot{\phi}_0S_0^2}{S^2}</math></center> | ||
| + | |||
| + | resultado que podemos sustituir en la ecuación de movimiento para θ | ||
| + | |||
| + | <center><math> \ddot{\theta}-\dot{\phi}_0^2S_0^4\frac{C}{S^3} = -\dfrac{3g}{2b}S</math></center> | ||
| + | |||
| + | Esta sería la ecuación de movimiento ya solo para este ángulo. | ||
| + | |||
| + | También podemos sustituir en la ley de conservación de la energía | ||
| + | |||
| + | <center><math>E=\frac{mb^2}{6}\dot{\theta}^2+\frac{3L_{0z_1}^2}{mb^2S^2}-\frac{mgb}{2}C</math></center> | ||
| + | |||
| + | que nos permite despejar la velocidad angular para cada valor del ángulo. | ||
| + | |||
| + | ===Movimiento cónico=== | ||
| + | Si se desea que la barra mantenga constante su inclinación, debe anularse la derivada <math>\dot{\theta}</math>, lo que nos da la condición | ||
| + | |||
| + | <center><math> -\dot{\phi}^2SC = -\dfrac{3g}{2b}S</math></center> | ||
| + | |||
| + | y por tanto | ||
| + | |||
| + | <center><math>\dot{\phi}=\sqrt{\dfrac{3g}{2bC}}</math></center> | ||
| + | |||
| + | Como el coseno vale como máximo 1, existe una velocidad angular mínima para poder conseguir una inclinación constante. | ||
| + | |||
| + | [[Categoría:Problemas de dinámica del sólido rígido (CMR)]] | ||
última version al 21:48 9 ene 2018
Contenido |
1 Enunciado
Una barra homogénea de 1kg de masa y 1m de longitud está suspendida del techo por dos soportes muy ligeros, uno de ellos está articulado a un punto A, situado a 20cm de un extremo de la barra y el otro está articulado sin rozamiento en el otro extremo O.
- Determine la fuerza que ejerce cada soporte en el equilibrio.
- En un momento dado, se rompe el soporte en A. Justo tras el corte, halle:
- La aceleración lineal del centro de masas de la barra, G.
- La aceleración angular de la barra
- La fuerza que realiza el soporte en O. ¿Cuánto ha aumentado o disminuido respecto a la situación de equilibrio?
- Suponga que la articulación en O es un par de revolución, de forma que solo puede moverse en el plano OXZ
- Obtenga las ecuacions de movimiento para el ángulo que forma con la vertical
- Halle las frecuencia de las pequeñas oscilaciones que realiza cuando se suelta desde una posición próxima a la vertical.
- Para el caso del enunciado, que se suelta desde la posición horizontal, calcule la fuerza que ejerce el soporte en O para cada ángulo θ
- Suponga ahora que la articulación en O es una rótula, de forma que la barra puede tanto variar su ángulo θ con la vertical como el ángulo ϕ alrededor de OZ.
- Determine las ecuaciones de movimiento para estos dos ángulos.
- Halle dos constantes de movimiento no triviales.
- Con ayuda de las constantes anteriores, halle una ecuación de movimiento para θ que no incluya a ϕ
- Calcule qué valor debe tener la velocidad angular
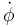 para la que la barra gire en torno a OZ manteniendo constante su ángulo θ con la vertical.
para la que la barra gire en torno a OZ manteniendo constante su ángulo θ con la vertical.
2 Equilibrio horizontal
En lo que sigue emplearemos varios sistemas de referencia. Tomamos como sistema fijo uno en el que el eje OZ1 es el vertical hacia arriba, el OY1 es el horizontal a lo largo de la barra y el OX1 el ortogonal a ambos según la regla de la mano derecha, es decir, dirigido hacia el observador.
En el estado de equilibrio, la barra está sometida a tres fuerzas:
- Su peso
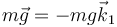 .
.
- La reacción en O,
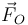 .
.
- La reacción en A,
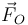 .
.
En principio, las dos fuerzas de reacción pueden tener cualquier dirección, pero es fácil ver que deben ser verticales, como el peso.
La condición de equilibrio de la barra la da el que el conjunto de fuerzas forme un sistema nulo

Como centro de reducción podemos elegir el que queramos pero, dado que el punto O va a ser fijo en lo que sigue, es mejor elegirlo ya.
Separando por componentes las fuerzas obtenemos las relaciones

y para los momentos respecto a OXZ

siendo
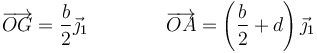
Vemos que este centro de reducción nos permite ignorar la fuerza en O, que se calcula posteriormente a partir del equilibrio de fuerzas.
Esto nos da
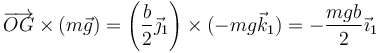
y
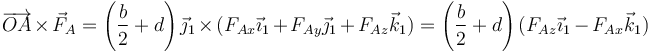
como el momento resultante debe anularse, debe ser
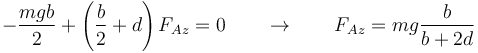
y

Esta ecuación no nos permite hallar las componentes de la fuerza según el eje OY, pero en ausencia de acciones externas, no hay razón para que no sean nulas.

Por el equilibrio de fuerzas obtenemos la fuerza en O

Estas fuerzas de reacción cumplen la ley de la palanca, ya que el producto de cada una por su distancia al CM da el mismo valor.

3 Corte del soporte
Una vez que se corta el soporte, el sistema deja de estar en equilibrio. Sobre las barras actúan dos fuerzas, siendo la de O diferente a la que había justo tras el corte.
La dinámica de la barra viene gobernada por el teorema de la cantidad de movimiento
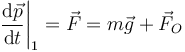
y por el teorema del momento cinético

De nuevo la elección de O como centro de reducción simplifica notablemente los cálculos.
En este caso, el peso provoca un par
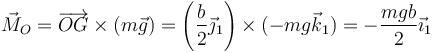
que provoca un giro en torno a OX1

donde esta cantidad ω será negativa ya que la barra va a descender.
El eje OX1 es un eje principal de inercia en este movimiento, por estar la barra confinada al plano x = 0. El momento de inercia respecto a este eje (que será un momento principal de inercia) vale
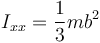
de forma que el momento cinético de la barra es
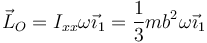
siendo su derivada respecto al tiempo
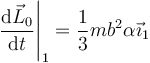
Igualando esto al momento del peso queda
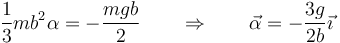
La aceleración del CM la obtenemos a partir de la expresión del campo de velocidades teniendo en cuenta que inicialmente la velocidad angular es nula
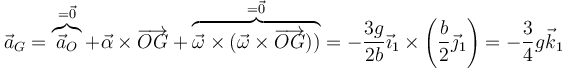
y esto nos permite hallar la fuerza que realiza la articulación de OA}
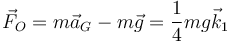
es decir, tira hacia arriba con 1/4 del peso.
La variación en la fuerza que ejerce este soporte por romper el otro es
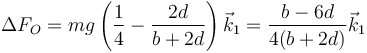
4 Oscilaciones verticales
4.1 Ecuación de movimiento
Cuando la barra sigue su descenso se siguen aplicando las ecuaciones anteriores, pero el momento del peso va cambiando ya que la distancia de O a la recta soporte depende de θ
En el sistema fijo, la posición del CM para cada ángulo con la vertical es

donde hemos usado las abreviaturas

siendo el momento del peso

Puesto que la rotación se produce en torno al eje OX1 se siguen cumpliendo las expresiones para el momento cinético
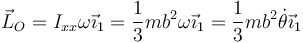
y para su derivada
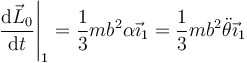
Igualando esta derivada al momento del peso queda
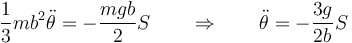
4.2 Pequeñas oscilaciones
Si el péndulo está cerca de la vertical, puede emplearse la aproximación

lo que reduce la ecuación de movimiento a
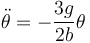
Esta es la ecuación de un oscilador armónico de frecuencia
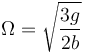
4.3 Fuerza en el soporte
Como en el caso horizontal se cumple
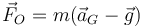
pero ahora la aceleración del CM incluye un término de aceleración normal
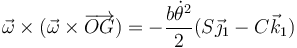
y otro de aceleración tangencial
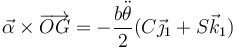
de manera que
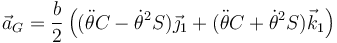
Siendo la reacción en O, por componentes,
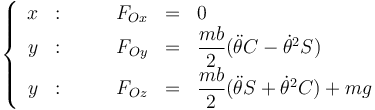
Ahora bien, este resultado está en función de θ y de sus derivadas, no solo de θ por lo que aun no es el resultado definitivo. Debemos poner las derivadas en función del ángulo. Para la segunda disponemos de la ecuación de movimiento
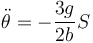


donde cada miembro cumple
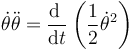
y

Por tanto llegamos a la ley de conservación
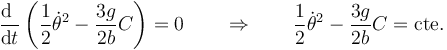
El valor de la constante sale de las condiciones iniciales
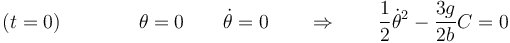
De aquí despejamos
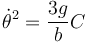
Tenemos por tanto que

Sustituimos en la expresión de la fuerza de reacción
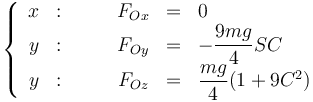
Vemos que la fuerza vertical va de 1/4 del peso en la posición horizontal a 5/2 del peso cuando pasa por la vertical. La fuerza horizontal, en cambio, es nula en estas dos posiciones y tiene un máximo cuando pasa por 45°, en que vale 9/8 del peso.
5 Movimiento tridimensional
5.1 Sistemas de referencia
Cuando consideramos los dos grados de libertad posibles el problema es máx complicado y se hace engorroso si solo se emplea el sistema de referencia fijo. Por ello, realizaremos el análisis completo empleando tres sistemas de referencia:
- El sistema fijo 1, con el eje OZ1 vertical
- El sistema ligado 2, en el que la barra va en la dirección del eje OZ2 negativo
- Un sistema intermedio 0, que está girado un ángulo ϕ en torno a OZ1 = OZ0 de manera que la barra se encuentre en todo momento en el plano OY0Z0
De esta forma obtendremos una solución que se puede expresar en términos más simples y de la cual podemos hallar, como casos particulares, as que acabamos de obtener.
La relación entre las bases de estos sistemas de referencia es, del fijo al intermedio

siendo la velocidad y aceleraciones angulares de este movimiento

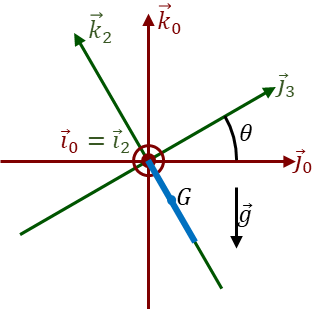
| Vista cenital | Vista frontal |
|---|---|
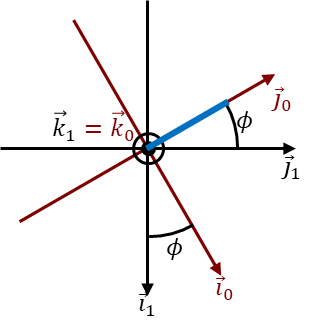
| 
|
La relación entre el sistema intermedio y el ligado al sólido la dan las relaciones
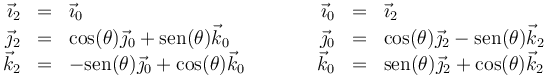
siendo la velocidad y aceleraciones angulares del movimiento {20}

5.2 Teorema del momento cinético
De nuevo, la forma más directa de llegar a las ecuaciones de movimiento es mediante el teorema del momento cinético, empleando como centro de reducción el punto fijo O. Respecto a este punto se cumple

El momento cinético posee una expresión sencilla en el sistema 2, ya que en este los ejes cartesianos son ejes principales. Se cumple
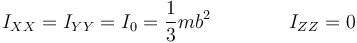
Por tanto, en este sistema
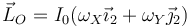
Las componentes de la velocidad angular en la base 2 las obtenemos mediante la composición de velocidades angulares

por lo que

y
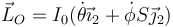
A la hora de derivar esta expresión debemos tener en cuenta que los vectores de la base dependen del tiempo, por lo que debemos emplear la fórmula de Poisson
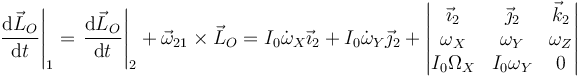
Separando por componentes e igualando al momento de las fuerzas queda
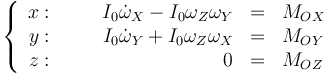
En el segundo miembro aparecen las componentes del momento de las fuerzas (el peso, en este caso), expresadas en la base 2.
La posición del CM en esta base es simplemente

mientras que el peso se escribe

lo que nos da un momento
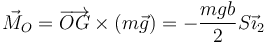
y llegamos a las ecuaciones
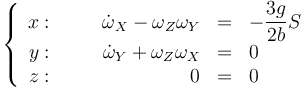
Si ahora sustituimos las componentes de la velocidad angular y sus derivadas llegamos a
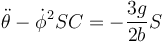
y
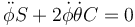
Estas son las ecuaciones que gobiernan la orientación de la varilla. Son ecuaciones no lineales cuya solución completa requiere el uso de ordenador.
Como caso particular vemos que si la varilla oscila en un plano vertical inmóvil (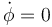 ) la primera ecuación se reduce a la que ya obtvimos
) la primera ecuación se reduce a la que ya obtvimos
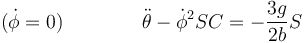
5.3 Teorema de la cantidad de movimiento
Como en el caso del movimiento plano, se cumple que
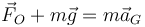
Esta ecuación nos permite calcular la fuerza ejercida sobre el soporte una vez que hemos determinado el movimiento del CM.

5.4 Constantes de movimiento
En este sistema tenemos dos constantes de movimiento no triviales. Las podemos calcular integrando las ecuaciones anteriores o mediante análisis de las magnitudes físicas. Antes empleamos el primer camino, ahora usaremos el segundo.
5.4.1 Componente vertical del momento cinético
La única fuerza que produce momento respecto del punto O, que tiene una dirección puramente vertical. Esto implica que su momento es puramente horizontal
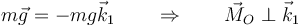
y por tanto la componente del momento cinético en dicha dirección es constante
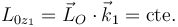
Se trata de expresar ahora este resultado en función de las variables del sistema. Según hemos dicho, el momento cinético tiene la expresión

y por tanto, la cantidad que es constante es

Para los productos escalares usamos las relaciones entre las bases que enunciamos antes

y
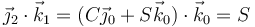
Como además
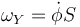
Llegamos a la constante de movimiento
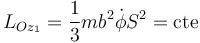
Podíamos haber llegado a este resultado integrando la segunda de las ecuaciones de movimiento.
El valor de la constante lo obtenemos de las condiciones iniciales.

5.4.2 Energía mecánica
Este sistema es conservativo, ya que sobre él actúan solo dos fuerzas:
- el peso, que deriva de un potencial,
- la reacción en O, que por actuar sobre un punto de velocidad nula no modifica la energía mecánica del sistema.
Por tanto
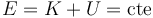
siendo la energía cinética

y la potencial
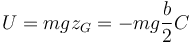
lo que nos da la constante
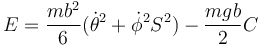
5.5 Ecuación de movimiento reducida
La conservación de la componente del momento cinético nos permite expresar 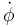 en función del ángulo θ
en función del ángulo θ

resultado que podemos sustituir en la ecuación de movimiento para θ

Esta sería la ecuación de movimiento ya solo para este ángulo.
También podemos sustituir en la ley de conservación de la energía

que nos permite despejar la velocidad angular para cada valor del ángulo.
5.6 Movimiento cónico
Si se desea que la barra mantenga constante su inclinación, debe anularse la derivada  , lo que nos da la condición
, lo que nos da la condición
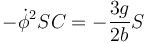
y por tanto
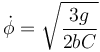
Como el coseno vale como máximo 1, existe una velocidad angular mínima para poder conseguir una inclinación constante.





