Péndulo formado por barra y disco (GIE)
De Laplace
(Página creada con '==Enunciado== Se tiene un péndulo compuesto, formado por una barra homogénea, de longitud <math>b=1.20\,\mathrm{m}</math> y masa <math>m_1=1.5\,\mathrm{kg}</math> en cuyo extr…') |
|||
| (2 ediciones intermedias no se muestran.) | |||
| Línea 10: | Línea 10: | ||
Tómese <math>g=10\,\mathrm{m}/\mathrm{s}^2</math> | Tómese <math>g=10\,\mathrm{m}/\mathrm{s}^2</math> | ||
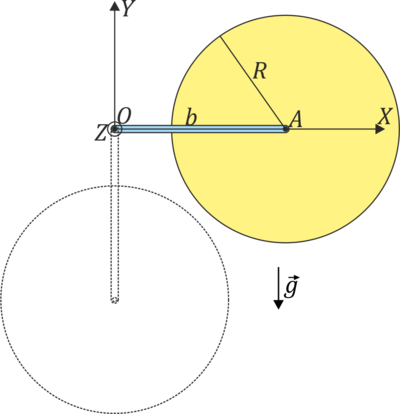
<center>[[Archivo:pendulo-barra-disco.png|400px]]</center> | <center>[[Archivo:pendulo-barra-disco.png|400px]]</center> | ||
| + | ==Centro de masas== | ||
| + | <center><math>\overrightarrow{OG}=\frac{m_1\overrightarrow{OG}_1+m_1\overrightarrow{OG}_2}{m_1+m_2}=\frac{1.5(0.60\vec{\imath})+3(1.2\vec{\imath})}{1.5+3.0}\mathrm{m}=1.0\,\vec{\imath}\,\mathrm{m}</math></center> | ||
| + | |||
| + | Hacemos | ||
| + | |||
| + | <center><math>d_G=|\overrightarrow{OG}|=1.00\,\mathrm{m}</math></center> | ||
| + | ==Momentos de inercia== | ||
| + | ===Respecto a OZ=== | ||
| + | Aplicando el teorema de Steiner a los dos sólidos: | ||
| + | <center><math>I_{zz}=I_{1zz}+I_{2zz}=\left(\frac{1}{12}m_1b^2+m_1\left(\frac{b}{2}\right)^2\right)+\left(\frac{1}{2}m_2R^2+m_2b^2\right)=6.00\mathrm{kg}\cdot\mathrm{m}^2</math></center> | ||
| + | ===Respecto a OX=== | ||
| + | Aplicando el teorema de la figura plana: | ||
| + | <center><math>I_{xx}=I_{1xx}+I_{2xx}=0+\frac{1}{4}m_2R^2=0.48\mathrm{kg}\cdot\mathrm{m}^2</math></center> | ||
| + | ===Respecto a OY=== | ||
| + | Aplicando el teorema de Steiner y el de la figura plana:<center><math>I_{yy}=I_{1yy}+I_{2yy}=\left(\frac{1}{12}m_1b^2+m_1\left(\frac{b}{2}\right)^2\right)+\left(\frac{1}{4}m_2R^2+m_2b^2\right)=5.52\mathrm{kg}\cdot\mathrm{m}^2</math></center> | ||
| + | |||
| + | Se cumple que | ||
| + | |||
| + | <center><math>I_{xx}+I_{yy}=I_{zz}</math></center> | ||
| + | ==Paso por la vertical== | ||
| + | ===Velocidad angular=== | ||
| + | Por conservación de la energía mecánica | ||
| + | |||
| + | <center><math>\frac{1}{2}I_{zz}|\vec{\omega}|^2+m g \overbrace{h_G}^{=-d_G} =0\qquad\Rightarrow\qquad |\omega|=\sqrt{\frac{2mgd_G}{I_{zz}}}=\sqrt{\frac{2\times 4.5\times 10\times 1}{6}}\,\frac{\mathrm{rad}}{\mathrm{s}}=\sqrt{15}\,\frac{\mathrm{rad}}{\mathrm{s}}=3.87\,\frac{\mathrm{rad}}{\mathrm{s}}</math></center> | ||
| + | |||
| + | Vectorialmente | ||
| + | |||
| + | <center><math>\vec{\omega}=-3.87\,\frac{\mathrm{rad}}{\mathrm{s}}\vec{k}</math></center> | ||
| + | ===Fuerza en A=== | ||
| + | <center><math>\vec{F}_A=-m_2\vec{g}+m_2\frac{|\vec{v}_{G2}|^2}{b}\vec{k}=m_2(g+|\vec{\omega}^2|b)\vec{k}=+84\,\mathrm{N}\,\vec{k}</math></center> | ||
| + | ===Fuerza en O=== | ||
| + | <center><math>\vec{F}_O=-m\vec{g}+m\frac{|\vec{v}_{G}|^2}{d_G}\vec{k}=m(g+|\vec{\omega}^2|d_G)\vec{k}=+112.5\,\mathrm{N}\,\vec{k}</math></center> | ||
| + | ==Disco de perfil== | ||
| + | El cálculo sería igual pero con <math>I_{yy}</math> en lugar de <math>I_{zz}</math>. Como <math>I_{yy}< I_{zz}</math> resulta una velocidad angular mayor al pasar por la vertical y por tanto también mayores fuerzas en A y en O. Concretamente | ||
| + | |||
| + | <center><math>|\vec{\omega}|=4.04 \,\frac{\mathrm{rad}}{\mathrm{s}}\qquad\qquad |\vec{F}_A|=88.7\,\mathrm{N}\qquad\qquad |\vec{F}_O|=118.4\,\mathrm{N}</math></center> | ||
| + | |||
| + | [[Categoría:Problemas de dinámica del sólido rígido (GIE)]] | ||
última version al 18:22 8 ene 2018
Contenido |
1 Enunciado
Se tiene un péndulo compuesto, formado por una barra homogénea, de longitud 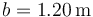 y masa
y masa 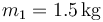 en cuyo extremo A se encuentra ensartado un disco de masa
en cuyo extremo A se encuentra ensartado un disco de masa  y radio
y radio 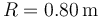 . La barra está articulada en su otro extremo O a un punto fijo. Esta articulación permite el movimiento solo en el plano vertical coplanario a la varillo y al disco. Inicialmente el péndulo está sujeto en reposo y con su varilla horizontal
. La barra está articulada en su otro extremo O a un punto fijo. Esta articulación permite el movimiento solo en el plano vertical coplanario a la varillo y al disco. Inicialmente el péndulo está sujeto en reposo y con su varilla horizontal
- Determine la posición del CM del péndulo, para la posición inicial, empleando los ejes indicados.
- Calcule el momento de inercia del péndulo respecto al eje OX, al OY y al OZ.
- Suponga que, estando el péndulo en la posición horizontal en reposo, se suelta. Para el instante en que pasa por la vertical…
- ¿Cuánto vale la velocidad angular del péndulo?
- ¿Qué fuerza ejerce el soporte del disco en A?
- ¿Qué fuerza ejerce el soporte del péndulo en O?
- Si el disco, en lugar de ser coplanario al plano de movimiento, fuera perpendicular a él (es decir, que en la figura lo veríamos de perfil, como una línea, prolongación de la varilla), al pasar por la vertical el péndulo su velocidad angular ¿sería mayor, menor, o igual a la del apartado anterior? ¿Por qué?
Tómese 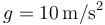
2 Centro de masas
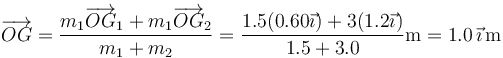
Hacemos
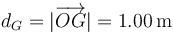
3 Momentos de inercia
3.1 Respecto a OZ
Aplicando el teorema de Steiner a los dos sólidos:
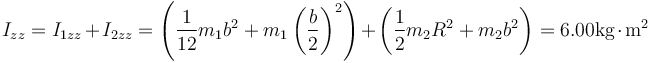
3.2 Respecto a OX
Aplicando el teorema de la figura plana:
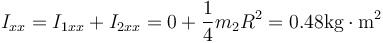
3.3 Respecto a OY
Aplicando el teorema de Steiner y el de la figura plana: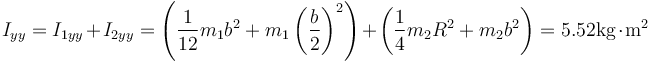
Se cumple que
4 Paso por la vertical
4.1 Velocidad angular
Por conservación de la energía mecánica

Vectorialmente
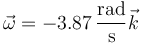
4.2 Fuerza en A
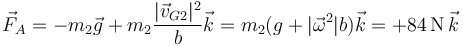
4.3 Fuerza en O
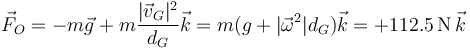
5 Disco de perfil
El cálculo sería igual pero con Iyy en lugar de Izz. Como Iyy < Izz resulta una velocidad angular mayor al pasar por la vertical y por tanto también mayores fuerzas en A y en O. Concretamente