Partícula en una superficie cónica (GIE)
De Laplace
(Diferencias entre revisiones)
(Página creada con '==Enunciado== Una partícula de masa m se encuentra obligada a moverse sobre la superficie interior de un cono recto, de eje vertical y cuyo semiángulo en el vértice mide β. …') |
|||
| Línea 2: | Línea 2: | ||
Una partícula de masa m se encuentra obligada a moverse sobre la superficie interior de un cono recto, de eje vertical y cuyo semiángulo en el vértice mide β. La partícula puede deslizar sin rozamiento sobre esta superficie y está sometido a la acción del peso, que va en la dirección vertical. | Una partícula de masa m se encuentra obligada a moverse sobre la superficie interior de un cono recto, de eje vertical y cuyo semiángulo en el vértice mide β. La partícula puede deslizar sin rozamiento sobre esta superficie y está sometido a la acción del peso, que va en la dirección vertical. | ||
Se desea que la partícula describa uniformemente circunferencias horizontales a una altura h respecto al vértice. Con ayuda de las coordenadas cilíndricas y la base asociada a ellas, | Se desea que la partícula describa uniformemente circunferencias horizontales a una altura h respecto al vértice. Con ayuda de las coordenadas cilíndricas y la base asociada a ellas, | ||
| - | <center>[[Archivo:particula-en-cono.png]]</center> | + | <center>[[Archivo:particula-en-cono.png|400px]]</center> |
# ¿Qué rapidez <math>v_0</math> debe comunicársele a la partícula, en función de la altura h? | # ¿Qué rapidez <math>v_0</math> debe comunicársele a la partícula, en función de la altura h? | ||
# ¿Cuánto vale, en módulo, la reacción de la superficie cónica en este movimiento? | # ¿Cuánto vale, en módulo, la reacción de la superficie cónica en este movimiento? | ||
Revisión de 18:41 27 nov 2017
Enunciado
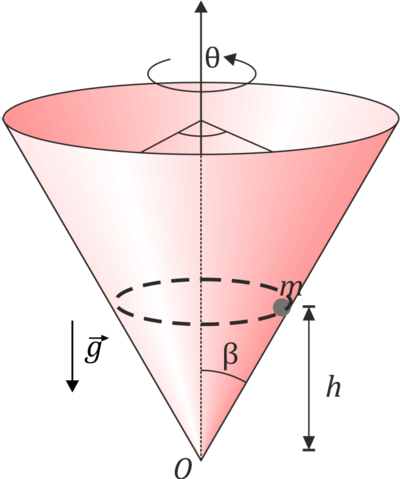
Una partícula de masa m se encuentra obligada a moverse sobre la superficie interior de un cono recto, de eje vertical y cuyo semiángulo en el vértice mide β. La partícula puede deslizar sin rozamiento sobre esta superficie y está sometido a la acción del peso, que va en la dirección vertical. Se desea que la partícula describa uniformemente circunferencias horizontales a una altura h respecto al vértice. Con ayuda de las coordenadas cilíndricas y la base asociada a ellas,
- ¿Qué rapidez v0 debe comunicársele a la partícula, en función de la altura h?
- ¿Cuánto vale, en módulo, la reacción de la superficie cónica en este movimiento?
- ¿Cuánto vale la proporción E/U entre la energía mecánica y la potencial para este movimiento circular? Tómese como origen de energía potencial el vértice del cono.
- Exprese, en la base de las coordenadas cilíndricas:
- La cantidad de movimiento. ¿Es constante?
- El momento cinético respecto a O. ¿Es constante?
- La fuerza resultante sobre la partícula
- El momento de las fuerzas sobre la partícula.





