Traslaciones de un sólido rígido
De Laplace
| Línea 72: | Línea 72: | ||
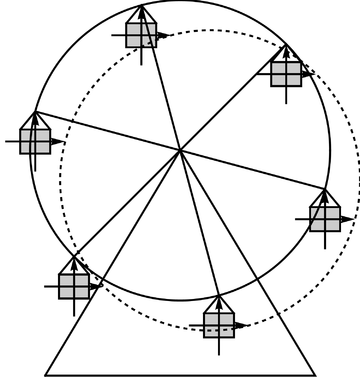
{{ejemplo|Consideremos el caso de las vagonetas de una noria circular. Si despreciamos el po-sible movimiento pendular, cada una de las cabinas describe una traslación permanente, no un movimiento de rotación. | {{ejemplo|Consideremos el caso de las vagonetas de una noria circular. Si despreciamos el po-sible movimiento pendular, cada una de las cabinas describe una traslación permanente, no un movimiento de rotación. | ||
| - | <center>[[Archivo:noria-traslacion.gif]]{{qquad}}[[Archivo:noria-traslacion.png]]</center> | + | <center>[[Archivo:noria-traslacion.gif]]{{qquad}}[[Archivo:noria-traslacion.png|360px]]</center> |
La orientación de los ejes ligados a una cabina permanece constante y todos sus puntos describen movimientos circulares paralelos. | La orientación de los ejes ligados a una cabina permanece constante y todos sus puntos describen movimientos circulares paralelos. | ||
}} | }} | ||
[[Categoría:Cinemática del sólido rígido (CMR)]] | [[Categoría:Cinemática del sólido rígido (CMR)]] | ||
última version al 11:47 27 oct 2017
Contenido |
1 Concepto de traslación
Una traslación es un movimiento en el que todos los puntos experimentan el mismo desplazamiento, preservándose la orientación del sólido
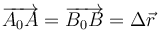
Esta condición implica que el vector de posición relativa entre dos puntos cualesquiera es el mismo tras la traslación que antes de ella
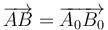
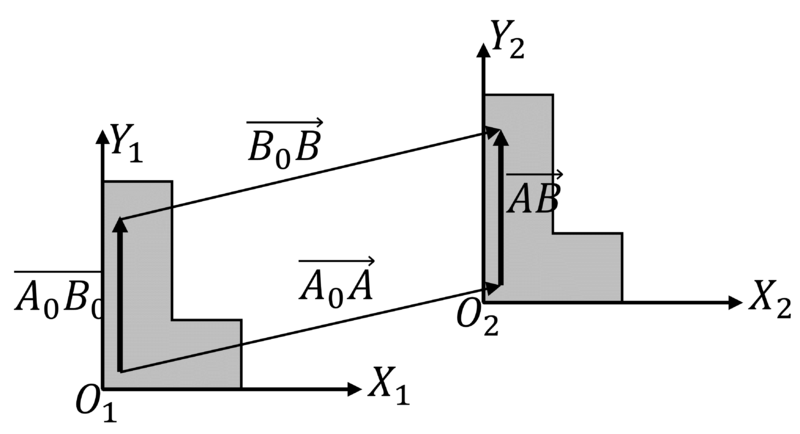
y por tanto, que el sistema de ejes ligado conserva su orientación respecto al fijo, es decir que el eje OX2 es paralelo al OX1, el OY2 al OY1 y así sucesivamente.
2 Traslaciones finitas
En términos de las componentes cartesianas, una traslación se calcula sumando las componentes del desplazamiento
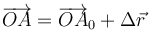
Empleando los sistemas de referencia fijo y ligado tenemos que en el instante inicial tomamos los dos sistemas como coincidentes, de forma que las coordenadas de cada punto son iguales en ambos sistemas
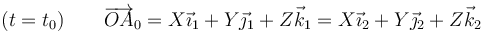
Tras la traslación, las componentes en el sistema ligado siguen siendo las mismas, pero e el sistema fijo han cambiado
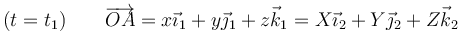
siendo la relación entre ellas las componentes del desplazamiento
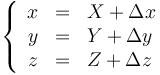
o, en forma matricial
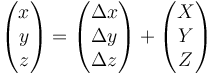
Una traslación finita no implica que en los instantes intermedios el sólido esté efectuando una traslación. Por ejemplo un disco que rueda sobre el suelo al completar una vuelta ha efectuado una traslación finita, ya que todos sus puntos han avanzado una distancia 2πR, pero en cada instante no solo se traslada sino que también gira.
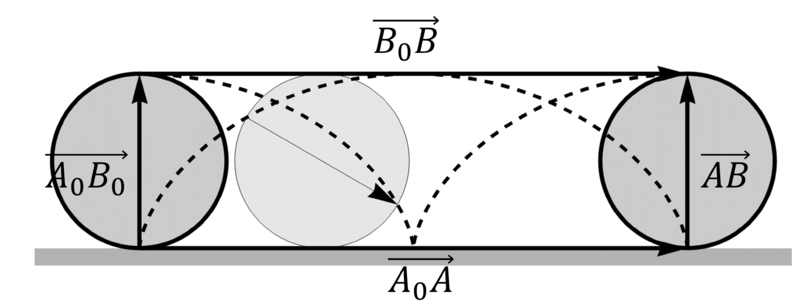
3 Traslaciones instantáneas
Una traslación instantánea es la que ocurre entre dos instantes sucesivos, t0 y t0 + dt. En este caso, los desplazamientos de todas las partículas son diferenciales e iguales entre sí
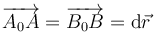
por lo cual la velocidad instantánea de todas las partículas es idéntica
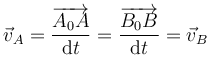
Hay que remarcar que esto es lo que ocurre en un instante concreto. De que un só-lido realice una traslación instantánea en un momento dado no podemos deducir que lo vaya a hacer en el siguiente.
En términos del sistema de referencia ligado puesto que su orientación no cambia en ese instante, se verifica
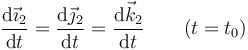
Equivalentemente, el movimiento de traslación se puede enunciar afirmando que si tres puntos no colineales del sólido tienen la misma velocidad, todos los demás también tienen la misma. No podemos afirmar que la aceleración de todas las partículas es la misma ya que el cálculo requiere una segunda derivada y por tanto conocer lo que ocurre en instantes posteriores.
4 Traslaciones permanentes
Un sólido experimenta una traslación permanente durante un cierto intervalo de tiempo cuando el movimiento en todo momento es una traslación instantánea.
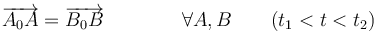
En una traslación permanente todas las partículas se mueven de la misma manera (aunque la velocidad en cada instante pueda ir cambiando)
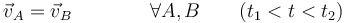
y por tanto las partículas describen trayectorias paralelas.
La orientación de los ejes ligados es constante en una traslación permanente.
En el caso de una traslación permanente sí podemos derivar con respecto al tiempo, con lo que resultan aceleraciones iguales para todas las partículas
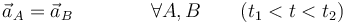
El que un sólido describa una traslación permanente no implica que describa un movimiento rectilíneo, ni un movimiento uniforme.
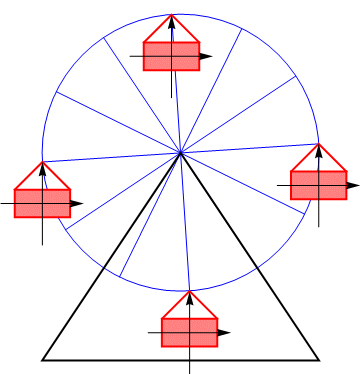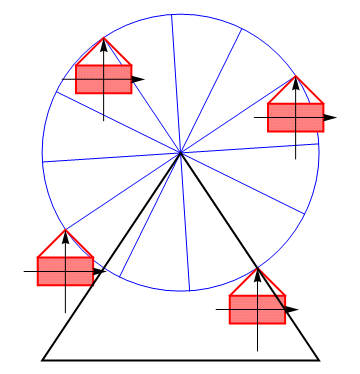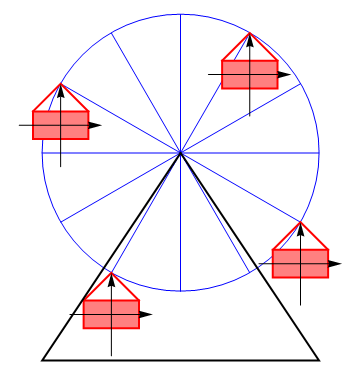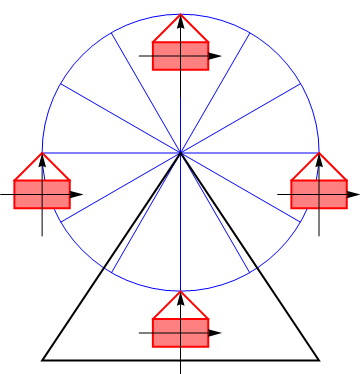
La orientación de los ejes ligados a una cabina permanece constante y todos sus puntos describen movimientos circulares paralelos.





