Traslaciones de un sólido rígido
De Laplace
| Línea 8: | Línea 8: | ||
<center><math>\overrightarrow{AB}=\overrightarrow{A_0B_0}</math></center> | <center><math>\overrightarrow{AB}=\overrightarrow{A_0B_0}</math></center> | ||
| - | <center>[[Archivo:traslacion-finita-L.png| | + | <center>[[Archivo:traslacion-finita-L.png|800px]]</center> |
y por tanto, que el sistema de ejes ligado conserva su orientación respecto al fijo, es decir que el eje <math>OX_2</math> es paralelo al <math>OX_1</math>, el <math>OY_2</math> al <math>OY_1</math> y así sucesivamente. | y por tanto, que el sistema de ejes ligado conserva su orientación respecto al fijo, es decir que el eje <math>OX_2</math> es paralelo al <math>OX_1</math>, el <math>OY_2</math> al <math>OY_1</math> y así sucesivamente. | ||
| Línea 37: | Línea 37: | ||
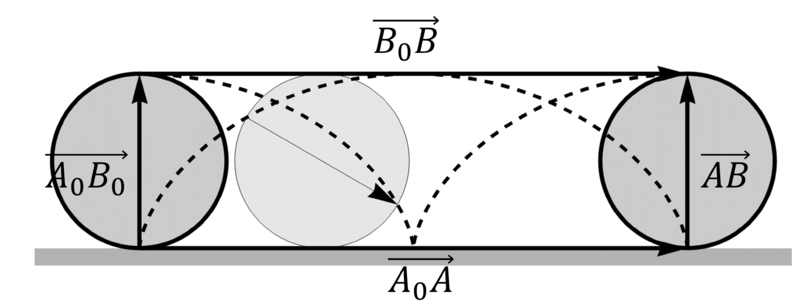
Una traslación finita no implica que en los instantes intermedios el sólido esté efectuando una traslación. Por ejemplo un disco que rueda sobre el suelo al completar una vuelta ha efectuado una traslación finita, ya que todos sus puntos han avanzado una distancia 2πR, pero en cada instante no solo se traslada sino que también gira. | Una traslación finita no implica que en los instantes intermedios el sólido esté efectuando una traslación. Por ejemplo un disco que rueda sobre el suelo al completar una vuelta ha efectuado una traslación finita, ya que todos sus puntos han avanzado una distancia 2πR, pero en cada instante no solo se traslada sino que también gira. | ||
| - | <center>[[Archivo:cicloide-traslacion.png]]</center> | + | <center>[[Archivo:cicloide-traslacion.png|800px]]</center> |
==Traslaciones instantáneas== | ==Traslaciones instantáneas== | ||
==Traslaciones permanentes== | ==Traslaciones permanentes== | ||
[[Categoría:Cinemática del sólido rígido (CMR)]] | [[Categoría:Cinemática del sólido rígido (CMR)]] | ||
Revisión de 09:35 27 oct 2017
Contenido |
1 Concepto de traslación
Una traslación es un movimiento en el que todos los puntos experimentan el mismo desplazamiento, preservándose la orientación del sólido
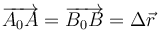
Esta condición implica que el vector de posición relativa entre dos puntos cualesquiera es el mismo tras la traslación que antes de ella
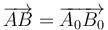
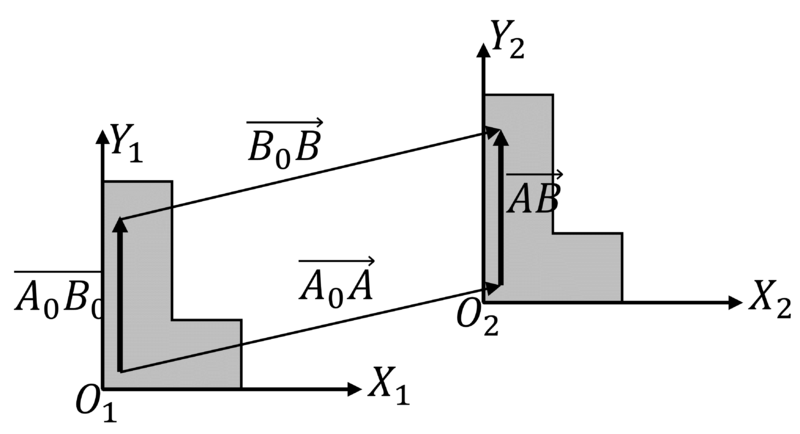
y por tanto, que el sistema de ejes ligado conserva su orientación respecto al fijo, es decir que el eje OX2 es paralelo al OX1, el OY2 al OY1 y así sucesivamente.
2 Traslaciones finitas
En términos de las componentes cartesianas, una traslación se calcula sumando las componentes del desplazamiento
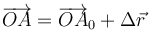
Empleando los sistemas de referencia fijo y ligado tenemos que en el instante inicial tomamos los dos sistemas como coincidentes, de forma que las coordenadas de cada punto son iguales en ambos sistemas
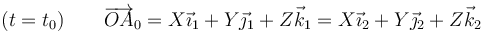
Tras la traslación, las componentes en el sistema ligado siguen siendo las mismas, pero e el sistema fijo han cambiado
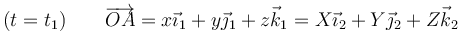
siendo la relación entre ellas las componentes del desplazamiento
\left\{ \begin{array}{rcl} x & = & X+ \Delta x \\ y & = & Y+ \Delta y \\ z & = & Z+ \Delta z \end{array}\right.
o, en forma matricial
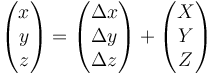
Una traslación finita no implica que en los instantes intermedios el sólido esté efectuando una traslación. Por ejemplo un disco que rueda sobre el suelo al completar una vuelta ha efectuado una traslación finita, ya que todos sus puntos han avanzado una distancia 2πR, pero en cada instante no solo se traslada sino que también gira.