Traslaciones de un sólido rígido
De Laplace
(Diferencias entre revisiones)
(Página creada con '==Concepto de traslación== ==Traslaciones finitas== ==Traslaciones instantáneas== ==Traslaciones permanentes== Categoría:Cinemática del sólido rígido (CMR)') |
|||
| Línea 1: | Línea 1: | ||
==Concepto de traslación== | ==Concepto de traslación== | ||
| + | Una traslación es un movimiento en el que todos los puntos experimentan el mismo desplazamiento, preservándose la orientación del sólido | ||
| + | |||
| + | <center><math>\overrightarrow{A_0A}=\overrightarrow{B_0B} = \Delta\vec{r}</math></center> | ||
| + | |||
| + | Esta condición implica que el vector de posición relativa entre dos puntos cualesquiera es el mismo tras la traslación que antes de ella | ||
| + | |||
| + | <center><math>\overrightarrow{AB}=\overrightarrow{A_0B_0}</math></center> | ||
| + | |||
| + | <center>[[Archivo:traslacion-finita-L.png]]</center> | ||
==Traslaciones finitas== | ==Traslaciones finitas== | ||
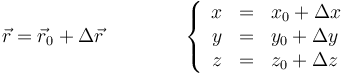
| + | En términos de las componentes cartesianas, una traslación se calcula sumando las componentes del desplazamiento | ||
| + | |||
| + | <center><math>\vec{r}=\vec{r}_0+\Delta \vec{r}\qquad\qquad \left\{ \begin{array}{rcl} x & = & x_0+ \Delta x \\ y & = & y_0+ \Delta y \\ z & = & z_0+ \Delta z \end{array}\right.</math></center> | ||
| + | |||
| + | |||
==Traslaciones instantáneas== | ==Traslaciones instantáneas== | ||
==Traslaciones permanentes== | ==Traslaciones permanentes== | ||
[[Categoría:Cinemática del sólido rígido (CMR)]] | [[Categoría:Cinemática del sólido rígido (CMR)]] | ||
Revisión de 10:00 27 oct 2017
Contenido |
1 Concepto de traslación
Una traslación es un movimiento en el que todos los puntos experimentan el mismo desplazamiento, preservándose la orientación del sólido
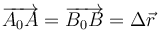
Esta condición implica que el vector de posición relativa entre dos puntos cualesquiera es el mismo tras la traslación que antes de ella
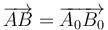
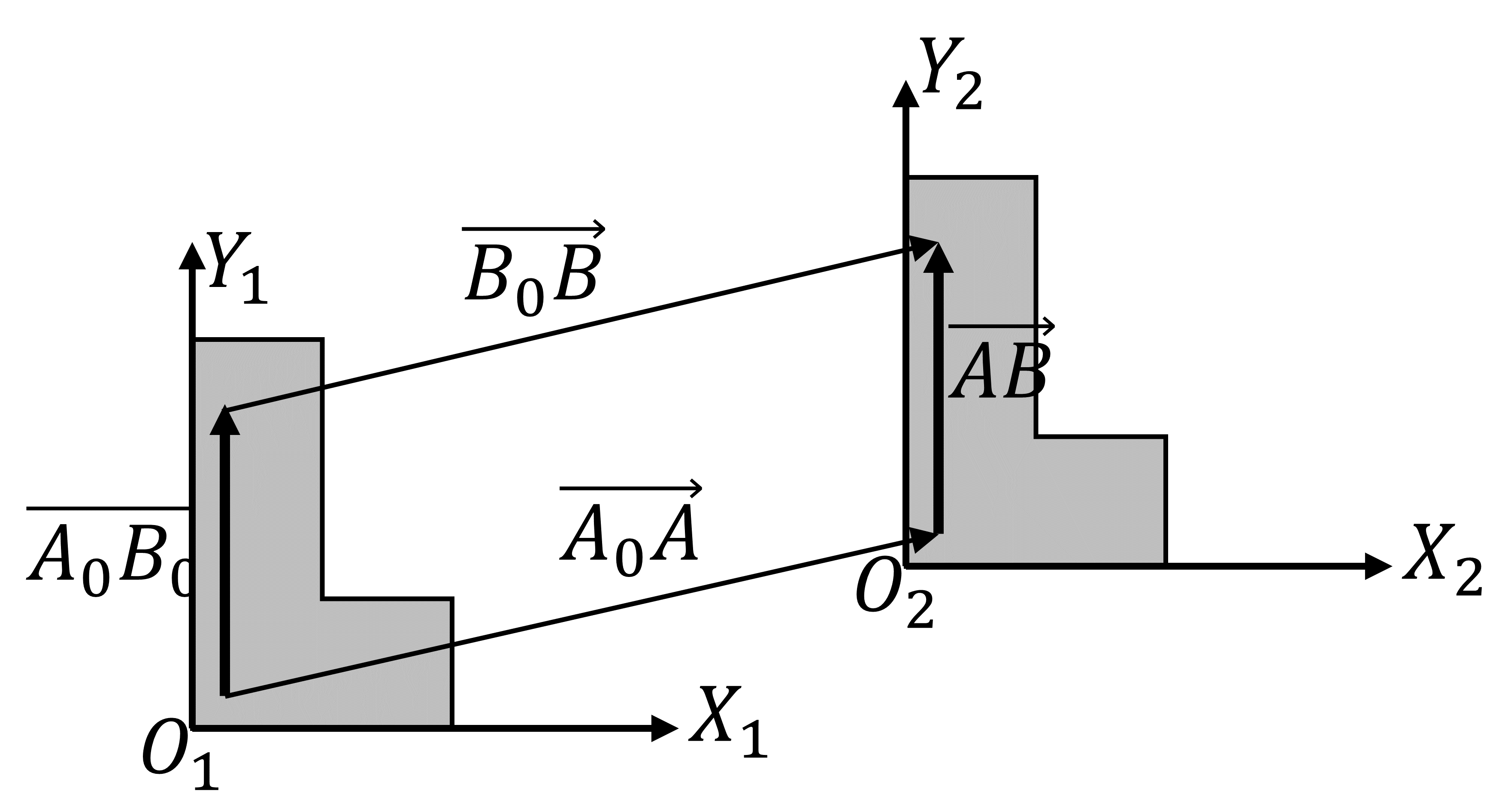
2 Traslaciones finitas
En términos de las componentes cartesianas, una traslación se calcula sumando las componentes del desplazamiento