Problemas de cinemática del sólido rígido (CMR)
De Laplace
(Diferencias entre revisiones)
(→Caso de rotación finita) |
|||
| Línea 9: | Línea 9: | ||
\vec{\jmath}_2 & = & 0.60\vec{\jmath}_1 + 0.80\vec{k}_1 \\ | \vec{\jmath}_2 & = & 0.60\vec{\jmath}_1 + 0.80\vec{k}_1 \\ | ||
\vec{k}_2 & = & 0.80\vec{\imath}_1 - 0.48\vec{\jmath}_1 + 0.368\vec{k}_1 \end{array}</math></center> | \vec{k}_2 & = & 0.80\vec{\imath}_1 - 0.48\vec{\jmath}_1 + 0.368\vec{k}_1 \end{array}</math></center> | ||
| - | |||
| - | |||
# Compruébese que la base es ortonormal. | # Compruébese que la base es ortonormal. | ||
# Determine un vector en la dirección del eje de rotación. | # Determine un vector en la dirección del eje de rotación. | ||
Revisión de 00:03 27 oct 2017
1 Traslación y rotación en el plano
En un movimiento plano, un sólido realiza una traslación 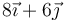 seguida de una rotación de 90° en torno a la nueva posición del origen de coordenadas. ¿Qué punto del plano está al final en la misma posición que al principio?
¿Cómo cambia el resultado si la rotación que sucede a la traslación es de un ángulo θ tal que tg(θ)=3\/4?
seguida de una rotación de 90° en torno a la nueva posición del origen de coordenadas. ¿Qué punto del plano está al final en la misma posición que al principio?
¿Cómo cambia el resultado si la rotación que sucede a la traslación es de un ángulo θ tal que tg(θ)=3\/4?
2 Caso de rotación finita
Tras una determinada rotación en torno al origen de coordenadas la base ligada al sólido se expresa en función de la base fija como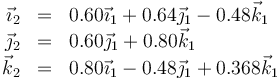
- Compruébese que la base es ortonormal.
- Determine un vector en la dirección del eje de rotación.
- Calcule el ángulo girado en torno a este eje (estudie el cambio de un vector perpendicular al eje).





