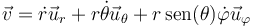Velocidad de una partícula (CMR)
De Laplace
| (2 ediciones intermedias no se muestran.) | |||
| Línea 104: | Línea 104: | ||
<center><math>\vec{T}=\cos(\phi-\theta)\vec{u}_\rho+\mathrm{sen}(\phi-\theta)\vec{u}_\theta</math></center> | <center><math>\vec{T}=\cos(\phi-\theta)\vec{u}_\rho+\mathrm{sen}(\phi-\theta)\vec{u}_\theta</math></center> | ||
| + | A modo de ejemplo, si consideramos una partícula describiendo un movimiento circular alrededor del origen, | ||
| + | |||
| + | <center><math>\rho = A = \mathrm{cte}\qquad\Rightarrow\qquad \dot{\rho}=0\qquad\qquad \dot{\theta}=\omega</math></center> | ||
| + | |||
| + | y resulta la velocidad | ||
| + | |||
| + | <center><math>\vec{v} = \overbrace{\dot{\rho}}^{0}\vec{u}_\rho + \overbrace{\rho}^{A}\overbrace{\dot{\theta}}^{\omega}\vec{u}_\theta = \omega A\vec{u}_\theta</math></center> | ||
| + | |||
| + | En un movimiento circular alrededor del origen la velocidad es puramente acimutal, ya que la partícula solo gira en torno al origen. | ||
| + | |||
| + | <center>[[Archivo:circular-polares.gif]]</center> | ||
| + | |||
| + | Sin embargo, el que la velocidad acimutal sea distinta de cero (que visto desde el origen se vea girar), no implica que el movimiento sea circular, ni siquiera curvo. | ||
| + | |||
| + | Consideremos el caso de una partícula que sigue un movimiento rectilíneo y uniforme a lo largo de una recta paralela al origen de forma que | ||
| + | |||
| + | <center><math>x = L\qquad y = v_0 t</math></center> | ||
| + | |||
| + | La expresión de este movimiento en polares es | ||
| + | |||
| + | <center><math>\rho = \sqrt{x^2+y^2} = \sqrt{L^2+v_0^2t^2}\qquad\qquad\theta=\,\mathrm{arctg}\left(\frac{y}{x}\right)=\,\mathrm{arctg}\left(\frac{v_0t}{L}\right)</math></center> | ||
| + | |||
| + | Las derivadas respecto al tiempo de estas dos magnitudes valen | ||
| + | |||
| + | <center><math>\dot{\rho}=\frac{v_0^2 t}{\sqrt{L^2+v_0^2 t^2}}\qquad \dot{\theta} = \frac{v_0L t}{L^2+v_0^2t^2}</math></center> | ||
| + | |||
| + | y esto nos da la velocidad instantánea | ||
| + | |||
| + | <center><math>\vec{v}=\frac{v_0^2 t\vec{u}_\rho+v_0Lt\vec{u}_\theta}{\sqrt{L^2+v_0^2t^2}}</math></center> | ||
| + | |||
| + | vemos que aunque el movimiento sea rectilíneo y uniforme, resulta una velocidad radial y una acimutal no nula. Para interpretarlo nos imaginamos a un observador situado en el origen de coordenadas, que apunte en todo momento a la partícula. Este observador ve a la partícula acercarse y alejarse (pasando por un mínimo justo cuando está en la perpendicular a la recta), y también ve cambiar la dirección de observación, lo que equivale a un giro. | ||
===Velocidad en cilíndricas=== | ===Velocidad en cilíndricas=== | ||
| Línea 124: | Línea 155: | ||
<center><math>\vec{v}=\dot{r}\vec{u}_r+r\dot{\theta}\vec{u}_\theta+r\,\mathrm{sen}(\theta)\dot{\varphi}\vec{u}_\varphi</math></center> | <center><math>\vec{v}=\dot{r}\vec{u}_r+r\dot{\theta}\vec{u}_\theta+r\,\mathrm{sen}(\theta)\dot{\varphi}\vec{u}_\varphi</math></center> | ||
| + | [[Categoría:Cinemática de la partícula (CMR)]] | ||
última version al 15:41 26 oct 2017
Contenido |
1 Definición
Se define la velocidad media en un intervalo de tiempo como el cociente entre el desplazamiento realizado y el intervalo de tiempo empleado en realizarlo.
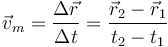
La velocidad instantánea de la partícula es el límite de la velocidad media cuando el intervalo de tiempo es muy pequeño
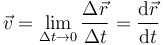
Es decir, la velocidad instantánea es la derivada de la posición respecto al tiempo. En Física, las derivadas respecto al tiempo suelen representarse con un punto sobre la magnitud
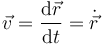
Si conocemos la velocidad instantánea a lo largo de un intervalo podemos calcular la posición como función del tiempo

2 Vector tangente
El vector velocidad va en la dirección tangente a la trayectoria. Esto permite definir el unitario tangente
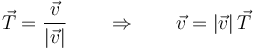
3 Movimiento en el plano
En el caso particular de una partícula que se mueve por el plano OXY, la velocidad posee solo dos componentes

por lo que el vector tangente está sobre dicho plano, formando un cierto ángulo con el eje OX

No hay que confundir este ángulo φ con la coordenada θ de polares. Las componentes del vector tangente se relacionan con las derivadas de las coordenadas a través de la proporcionalidad entre los vectores
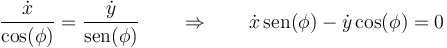
4 Rapidez y distancia recorrida
Al módulo de la velocidad se lo denomina rapidez o celeridad de la partícula. Mide el ritmo con el que se recorre la trayectoria y como tal se relaciona directamente con el parámetro arco
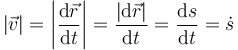
Esto permite determinar la distancia recorrida en un intervalo de tiempo dado
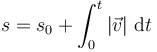
5 Componentes de la velocidad
En un sistema de referencia fijo, los vectores de la base cartesiana son constantes, por lo que
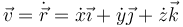
es decir, las componentes de la velocidad son las derivadas de las componentes de la posición.
6 Velocidad en función de parámetros
Si la posición no está dada explícitamente en función del tiempo, sino que conocemos la trayectoria en función de un parámetro θ para hallar la velocidad es preciso aplicar la regla de la cadena

A menudo, la posición no se indica en función de las coordenadas cartesianas, sino como función de 2 o más variables, θ, φ… (denominadas coordenadas generalizadas). En ese caso, se extiende la expresión anterior
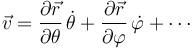
Si denominamos a las diferentes variables como 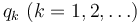 la expresión anterior se escribe
la expresión anterior se escribe
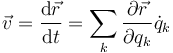
En ocasiones, la posición se expresa como función del tiempo y de una variable (dependiente implícitamente del tiempo). En ese caso, aplicamos que la derivada del tiempo respecto a sí mismo vale 1 (la velocidad del tiempo es un segundo por segundo) y queda
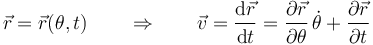
Nótese la diferencia entre la derivada total (d) y la parcial (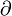 ).
).
Si depende de varias variables y del tiempo queda la fórmula general
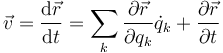
7 Velocidad en polares, cilíndricas y esféricas
7.1 Velocidad en polares
Cuando una partícula se mueve en el plano OXY su velocidad se encuentra confinada a este plano y tiene solo dos componentes
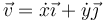
Por ser un vector de este plano podrá expresarse en la base polares. Obtenemos esta expresión derivando el vector de posición
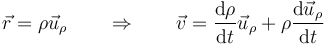
La segunda derivada no es nula ya que el vector radial acompaña a la partícula en su movimiento y por tanto depende del tiempo. La calculamos por la regla de la cadena
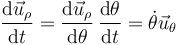
lo que nos da la velocidad

esto es, aunque la posición posee solo componente radial, la velocidad posee componente radial, debido al cambio en la distancia al origen y velocidad lateral, debido al cambio en la orientación del vector de posición.
La rapidez de la partícula en polares es el módulo de este vector
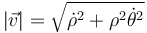
El vector tangente en estas coordenadas se calcula dividiendo la velocidad por su módulo. A su vez, si este vector forma un ángulo φ con el eje OX

forma uno φ − θ con el vector de posición
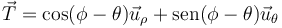
A modo de ejemplo, si consideramos una partícula describiendo un movimiento circular alrededor del origen,

y resulta la velocidad
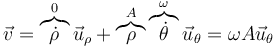
En un movimiento circular alrededor del origen la velocidad es puramente acimutal, ya que la partícula solo gira en torno al origen.
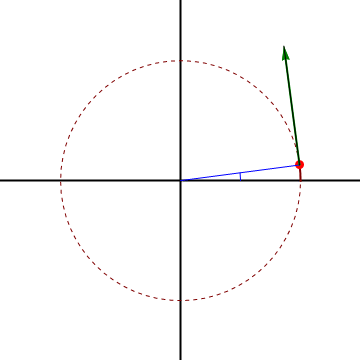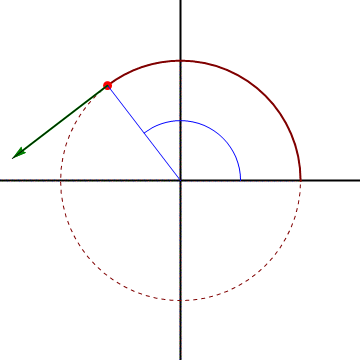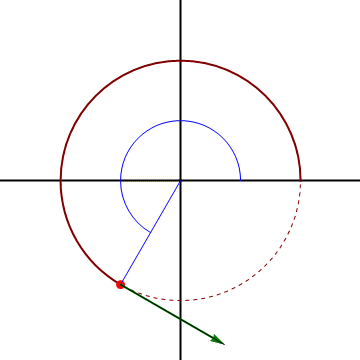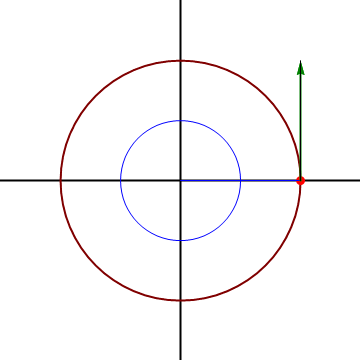
Sin embargo, el que la velocidad acimutal sea distinta de cero (que visto desde el origen se vea girar), no implica que el movimiento sea circular, ni siquiera curvo.
Consideremos el caso de una partícula que sigue un movimiento rectilíneo y uniforme a lo largo de una recta paralela al origen de forma que

La expresión de este movimiento en polares es

Las derivadas respecto al tiempo de estas dos magnitudes valen
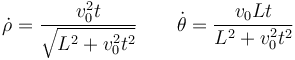
y esto nos da la velocidad instantánea
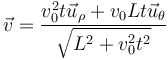
vemos que aunque el movimiento sea rectilíneo y uniforme, resulta una velocidad radial y una acimutal no nula. Para interpretarlo nos imaginamos a un observador situado en el origen de coordenadas, que apunte en todo momento a la partícula. Este observador ve a la partícula acercarse y alejarse (pasando por un mínimo justo cuando está en la perpendicular a la recta), y también ve cambiar la dirección de observación, lo que equivale a un giro.
7.2 Velocidad en cilíndricas
Al pasar a tres dimensiones en coordenadas cilíndricas, simplemente añadimos la componente vertical del movimiento
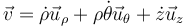
Así, en el caso del movimiento helicoidal uniforme
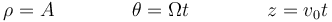
la velocidad posee dos componentes en cilíndricas
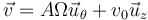
que indica que en este caso la velocidad forma un ángulo constante con la horizontal.
7.3 Velocidad en esféricas
El cálculo de la velocidad en esféricas se hace de manera análoga al caso de polares pero teniendo en cuenta que en este caso el vector 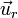 depende de las dos variables angulares θ y
depende de las dos variables angulares θ y  . El resultado es
. El resultado es