Posición de una partícula (CMR)
De Laplace
| (14 ediciones intermedias no se muestran.) | |||
| Línea 220: | Línea 220: | ||
Las coordenadas polares pueden extenderse a tres dimensiones añadiendo una tercera coordenada cartesiana, que sería la altura <math>z</math>. | Las coordenadas polares pueden extenderse a tres dimensiones añadiendo una tercera coordenada cartesiana, que sería la altura <math>z</math>. | ||
| - | <center>[[Archivo: | + | <center>[[Archivo:cilindricas.png|400px]]</center> |
<center><math>x = \rho\cos(\theta) \qquad y = | <center><math>x = \rho\cos(\theta) \qquad y = | ||
| Línea 260: | Línea 260: | ||
===Coordenadas esféricas=== | ===Coordenadas esféricas=== | ||
| - | Otra posible generalización consiste en convertir el plano OXY en el OXZ y girarlo alrededor del eje OZ. Añadimos entonces una tercera coordenada \varphi que representa el giro del vector de posición alrededor del eje OZ. De esta forma, las coordenadas cartesianas de la posición se expresan | + | Otra posible generalización consiste en convertir el plano OXY en el OXZ y girarlo alrededor del eje OZ. Añadimos entonces una tercera coordenada <math>\varphi</math> que representa el giro del vector de posición alrededor del eje OZ. De esta forma, las coordenadas cartesianas de la posición se expresan |
<center><math>\begin{array}{rcl} | <center><math>\begin{array}{rcl} | ||
| Línea 268: | Línea 268: | ||
\end{array}</math></center> | \end{array}</math></center> | ||
| - | <center>[[Archivo: | + | <center>[[Archivo:Base-esfericas.png|400px]]</center> |
Geométricamente, | Geométricamente, | ||
* <math>r</math>, ''coordenada radial'', varía en <math>[0,\infty)</math>, es la distancia al origen de coordenadas | * <math>r</math>, ''coordenada radial'', varía en <math>[0,\infty)</math>, es la distancia al origen de coordenadas | ||
| Línea 274: | Línea 274: | ||
* <math>\varphi</math>, ''coordenada acimutal'', varía en <math>[0,2\pi]</math>, representa el ángulo forma con OX la proyección del vector de posición con el plano OXY. En la superficie terrestre equivale a la longitud respecto al meridiano de Greenwich. | * <math>\varphi</math>, ''coordenada acimutal'', varía en <math>[0,2\pi]</math>, representa el ángulo forma con OX la proyección del vector de posición con el plano OXY. En la superficie terrestre equivale a la longitud respecto al meridiano de Greenwich. | ||
| - | <center>[[Archivo:Latitud.png]] [[Archivo:Esf-sup.png]]</center> | + | <center>[[Archivo:Latitud.png|300px]]{{qquad}}{{qquad}}[[Archivo:Esf-sup.png]]</center> |
En coordenadas esféricas, las superficies <math>r=\mathrm{cte.}</math> son esferas concéntricas, las <math>\theta=\mathrm{cte.}</math> son conos con vértice el origen y eje el OZ y las <math>\varphi=\mathrm{cte.}</math> son semiplanos verticales. | En coordenadas esféricas, las superficies <math>r=\mathrm{cte.}</math> son esferas concéntricas, las <math>\theta=\mathrm{cte.}</math> son conos con vértice el origen y eje el OZ y las <math>\varphi=\mathrm{cte.}</math> son semiplanos verticales. | ||
| Línea 281: | Línea 281: | ||
Las coordenadas esféricas llevan asociadas una base vectorial <math>\{\vec{u}_r,\vec{u}_\theta,\vec{u}_\varphi\}</math> dependiente de la posición, donde cada vector es el unitario en la dirección y sentido en que aumenta cada coordenada. | Las coordenadas esféricas llevan asociadas una base vectorial <math>\{\vec{u}_r,\vec{u}_\theta,\vec{u}_\varphi\}</math> dependiente de la posición, donde cada vector es el unitario en la dirección y sentido en que aumenta cada coordenada. | ||
| + | |||
| + | Si lo representamos sobre una superficie de una esfera, que podemos imaginar la terrestre, el unitario radial <math>\vec{u}_r</math> va hacia afuera de la esfera, el polar <math>\vec{u}_\theta</math> va hacia el sur y el acimutal <math>\vec{u}_\varphi</math> va hacia el este. | ||
La expresión de la base de esféricas en función de la canónica es más complicada que en cilíndricas | La expresión de la base de esféricas en función de la canónica es más complicada que en cilíndricas | ||
| Línea 286: | Línea 288: | ||
<center><math>\begin{array}{rcl} | <center><math>\begin{array}{rcl} | ||
\vec{u}_r&=&\mathrm{sen}\,\theta\,\cos\varphi\vec{\imath}+\mathrm{sen}\,\theta\,\mathrm{sen}\,\varphi\vec{\jmath}+\cos\theta\vec{k}\\ | \vec{u}_r&=&\mathrm{sen}\,\theta\,\cos\varphi\vec{\imath}+\mathrm{sen}\,\theta\,\mathrm{sen}\,\varphi\vec{\jmath}+\cos\theta\vec{k}\\ | ||
| - | \ | + | \vec{u}_{\theta}&=&\cos\theta\cos\varphi\vec{\imath}+\cos\theta\mathrm{sen}\,\varphi\vec{\jmath}-\mathrm{sen}\,\theta\vec{k}\\ |
| - | \ | + | \vec{u}_\varphi&=& -\mathrm{sen}\,\varphi\,\vec{\imath} + \cos\varphi \vec{\jmath} |
\end{array}</math></center> | \end{array}</math></center> | ||
| + | |||
| + | Estos vectores dependen de la posición a través de los ángulos <math>\theta</math> y <math>\varphi</math>, cumpliéndose las relaciones | ||
| + | |||
| + | <center><math>\frac{\partial\vec{u}_r}{\partial \theta}=\vec{u}_\theta\qquad\qquad \frac{\partial\vec{u}_r}{\partial \varphi}=\mathrm{sen}(\theta)\vec{u}_\varphi\qquad\qquad\frac{\partial\vec{u}_\theta}{\partial \theta}=-\vec{u}_r\qquad\qquad \frac{\partial\vec{u}_\theta}{\partial \varphi}=\cos(\theta)\vec{u}_\varphi\qquad\qquad\frac{\partial\vec{u}_\varphi}{\partial \theta}=\vec{0}\qquad\qquad \frac{\partial\vec{u}_\varphi}{\partial \varphi}=-\mathrm{sen}(\theta)\vec{u}_r-\cos(\theta)\vec{u}_\theta</math></center> | ||
==Ortonormalidad de las bases== | ==Ortonormalidad de las bases== | ||
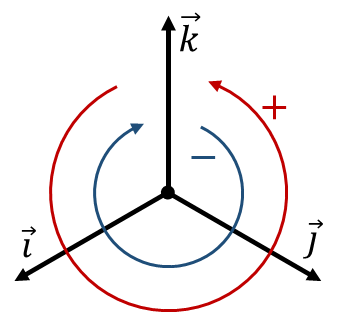
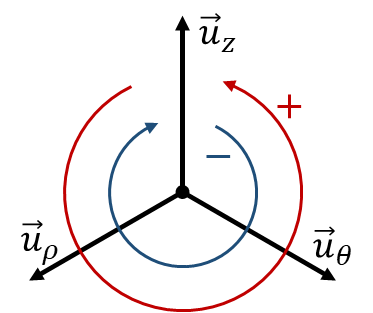
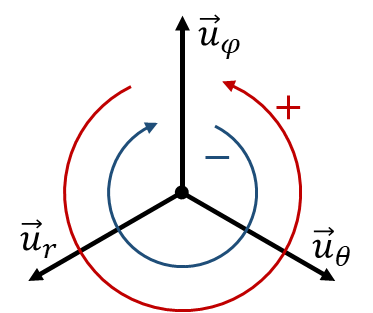
La base canónica <math>\left\{\vec{\imath},\vec{\jmath},\vec{k}\right\}</math>, la asociada a cilíndricas <math>\left\{\vec{u}_\rho,\vec{u}_\theta,\vec{u}_z\right\}</math> y la asociada a esféricas <math>\left\{\vec{u}_r,\vec{u}_\theta,\vec{u}_\varphi\right\}</math> son las tres ortonormales, es decir, los vectores de cada una son unitarios, son ortogonales con los otros dos vectores de la misma base y cumplen la regla de la mano derecha en el producto vectorial (siempre que se sitúen en el orden indicado). | La base canónica <math>\left\{\vec{\imath},\vec{\jmath},\vec{k}\right\}</math>, la asociada a cilíndricas <math>\left\{\vec{u}_\rho,\vec{u}_\theta,\vec{u}_z\right\}</math> y la asociada a esféricas <math>\left\{\vec{u}_r,\vec{u}_\theta,\vec{u}_\varphi\right\}</math> son las tres ortonormales, es decir, los vectores de cada una son unitarios, son ortogonales con los otros dos vectores de la misma base y cumplen la regla de la mano derecha en el producto vectorial (siempre que se sitúen en el orden indicado). | ||
| - | + | {| class="bordeado" | |
| - | [[Categoría:Cinemática (CMR)]] | + | |- |
| + | | [[Archivo:triedro-canonico.png]] | ||
| + | | [[Archivo:triedro-cilíndricas.png]] | ||
| + | | [[Archivo:triedro-esfericas.png]] | ||
| + | |- | ||
| + | | <math>\vec{\imath}\times\vec{\jmath}=\vec{k}</math> | ||
| + | | <math>\vec{u}_\rho\times\vec{u}_\theta=\vec{u}_z</math> | ||
| + | | <math>\vec{u}_r\times\vec{u}_\theta=\vec{u}_\varphi</math> | ||
| + | |} | ||
| + | [[Categoría:Cinemática de la partícula (CMR)]] | ||
última version al 15:40 26 oct 2017
Contenido |
1 Sistemas de referencia
En Mecánica Clásica se considera que el espacio es euclidiano, es decir, que podemos construir sistemas de referencia cartesianos que se extienden a todo el espacio.
Los puntos del espacio pueden etiquetarse mediante letras, O, P, Q,… Sin embargo, para operar con ellos, es conveniente emplear coordenadas, que no son más que etiquetas numéricas que identifican cada punto de forma unívoca.
Existen muchos sistemas de coordenadas posibles. Las más sencillas son las coordenadas cartesianas
Dado un punto del espacio, O, que tomamos como origen de coordenadas, tomamos tres planos que pasan por dicho punto y que sean ortogonales entre sí, que denominaremos XY, XZ e YZ. Definimos entonces las coordenadas cartesianas de cualquier otro punto como las distancias (con signo), x, y, z a estos planos coordenados (x la distancia al YZ, y al XZ, y z al XY).
Los planos se cortan en tres rectas, también ortogonales entre sí, que denominamos ejes de coordenadas OX, OY y OZ (o simplemente X, Y y Z).
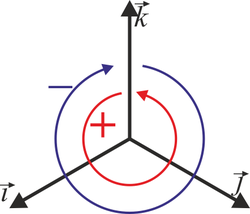
Los vectores unitarios tangentes a estos ejes forman una base ortonormal que denotamos como  .
.
Por ser ortonormales, verifican
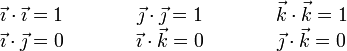
o, en forma de tabla:

| 
| 
| 
|
|---|---|---|---|

| 1 | 0 | 0 |

| 0 | 1 | 0 |

| 0 | 0 | 1 |
Esta base canónica es además dextrógira, esto es, verifica la regla de la mano derecha cuando los vectores se colocan en el orden  . Empleando el producto vectorial, esto se expresa
. Empleando el producto vectorial, esto se expresa
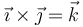
y análogamente para el resto de productos: positivo si se gira en sentido antihorario y negativo si se va en sentido horario en la figura. En forma de tabla:
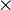
| 
| 
| 
|
|---|---|---|---|

| 
| 
| 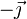
|

| 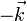
| 
| 
|

| 
| 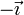
| 
|
En términos de esta base, cualquier vector podrá escribirse como una combinación lineal

La posición de cualquier punto P puede expresarse mediante su vector de posición, que es aquél que tiene como origen el de coordenadas y como extremo el punto P (es, por tanto, un vector ligado)
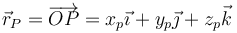
La posición relativa del punto Q respecto al punto P la da el vector que tiene por origen P y por extremo Q. Es inmediato obtener las componentes de este vector en la base cartesiana, conocidas las coordenadas cartesianas del origen y del extremo. Basta restarle las primeras a las segundas. Si P(xp,yp,zp) y Q(xq,yq,zq), el vector 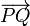 es:
es:
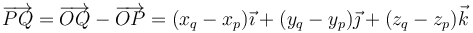
2 Posición, trayectoria y ley horaria
Una partícula material es, en mecánica, un modelo en el que un objeto se considera con masa, pero ocupando solo un punto del espacio. Se aplica al estudio de cuerpos cuyas dimensiones son mucho menores que las distancias que recorre o a puntos particulares de cuerpos extensos, como puede ser el centro de masas de un sistema.
2.1 Posición y desplazamiento
En su movimiento por el espacio, la posición de una partícula va cambiando de forma continua

aunque usualmente no se indica de forma explícita la dependencia con el tiempo.
Cuando la posición de una partícula se da de esta forma se dice que tenemos la ecuación horaria de su movimiento.
El desplazamiento de una partícula en un intervalo es la diferencia vectorial entre sus posiciones
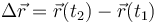
Cuando este desplazamiento es muy pequeño comparado con las distancias típicas recorridas, se dice que tenemos un desplazamiento diferencial, 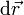 .
.
2.2 Trayectoria
A la curva que describe la partícula en su movimiento se la denomina la trayectoria de la partícula.
Una misma trayectoria puede ser escrita por una infinitud de ecuaciones horarias diferentes, dependiendo del ritmo con el que se recorra.
Para identificar una trayectoria independientemente del tiempo se suele describir la curva en forma paramétrica

siendo θ una variable continua que identifica de forma unívoca los puntos de la curva.
De entre los diferentes parámetros posibles, destaca el llamado parámetro arco o parámetro natural, s, que mide la distancia sobre la curva (en el caso de una carretera serían los puntos kilométricos). El parámetro arco se obtiene sumando las distancias diferenciales a lo largo de la trayectoria
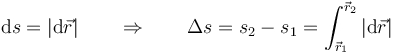
2.3 Ley horaria
Cuando se tiene la trayectoria parametrizada en términos de la distancia medida sobre la curva la descripción se completa indicando cómo cambia esta variable con el tiempo. Esta dependencia temporal se conoce como ley horaria:
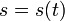
En el ejemplo de un coche que va de Sevilla a Granada, la ley horaria sería la hora a la que pasó por cada punto del camino sin prestar atención si en ese punto en concreto la carretera va hacia el sur o hacia el este.
Según esto, las ecuaciones horarias del movimiento pueden descomponerse en la trayectoria por un lado y la ley horaria por otro:
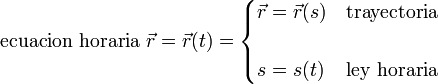
Si en lugar del parámetro arco, se describe la trayectoria con otra variable también se denomina ley horaria a la dependencia de esta variable con el tiempo. Así, en general:
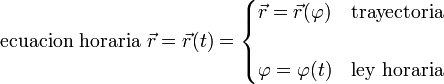
3 Movimiento en el plano
3.1 En coordenadas cartesianas
En el caso de que la partícula se mueva en el plano OXY, el vector de posición se reduce a solo dos componentes
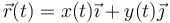
El movimiento en el plano tiene gran importancia teórica, ya que muchos movimientos destacados son planos (por ejemplo, las órbitas planetarias, o los movimientos de muchos engranajes), pero también por razones prácticas, ya que permite trazar fácilmente las trayectorias.
3.2 Coordenadas polares
En el caso de movimiento en un plano, es útil considerar las coordenadas polares para describir el movimiento de la partícula, {ρ,θ}. Estas coordenadas son la distancia al origen del sistema de referencia (ρ) y el ángulo que forma el vector de posición con el eje OX (θ).

y sus inversas

Las coordenadas polares llevan asociadas una base vectorial 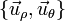 , que apuntan respectivamente en la dirección radial (en la que varía ρ) y acimutal (en la que varía θ). Esta base se relaciona con la canónica por el cambio de base
, que apuntan respectivamente en la dirección radial (en la que varía ρ) y acimutal (en la que varía θ). Esta base se relaciona con la canónica por el cambio de base
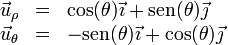 ó
ó 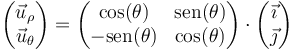
y su inverso
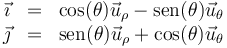 ó
ó 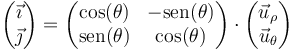
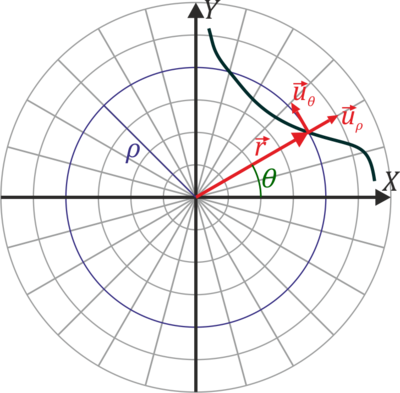
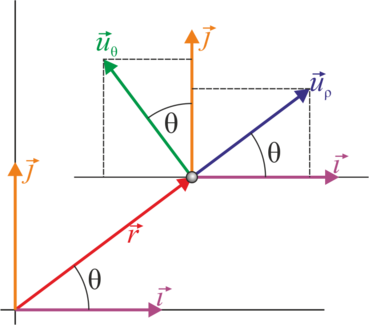
Los vectores unitarios en polares dependen de la posición. Aunque tengan el mismo nombre, el vector 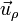 en un punto es diferente del vector
en un punto es diferente del vector 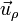 en otro. Por ello, hay que tener un cuidado infinito a la hora de operar con vectores en coordenadas polares.
en otro. Por ello, hay que tener un cuidado infinito a la hora de operar con vectores en coordenadas polares.
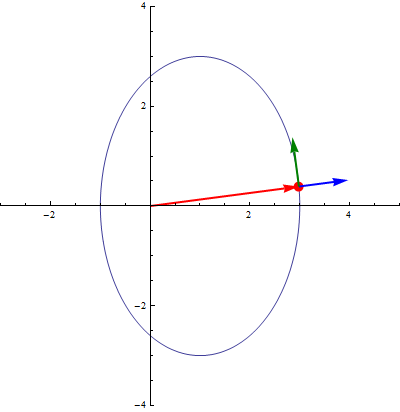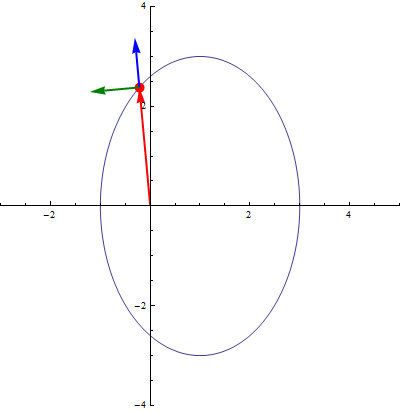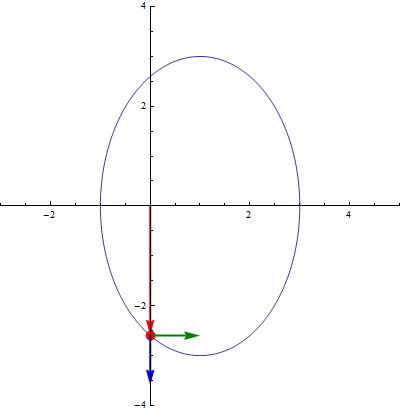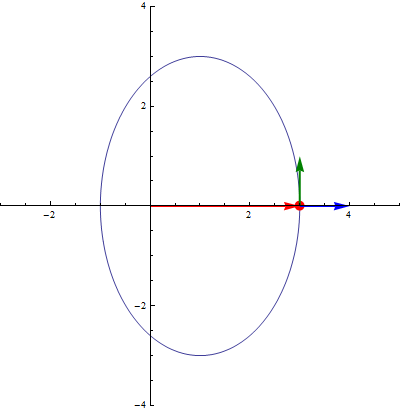
En particular, cuando consideramos el movimiento de una partícula, su posición, y por tanto los vectores de la base en polares, son funciones del tiempo. Por ello, cuando aparezca una derivada o una integral, habrá que tenerlos en cuenta. Sus derivadas respecto del tiempo valen
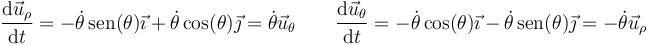
3.3 Posición en polares
Puesto que el vector 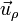 es el unitario en la dirección del vector de posición en el plano tenemos que la expresión de este en polares es
es el unitario en la dirección del vector de posición en el plano tenemos que la expresión de este en polares es
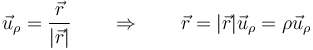
3.4 Componentes de un vector en polares
Dado cualquier vector en componentes cartesianas, sus componentes en polares se obtienen proyectando sobre esta base

3.5 Ejemplos de curvas en polares
Una trayectoria plana posee una expresión en coordenadas polares en las que ρ y θ dependen del tiempo, directamente o indirectamente a través de uno o varios parámetros.
La identificación de una trayectoria expresada en polares en ocasiones es sencilla. Así
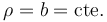
representa una circunferencia centrada en el origen.
La curva
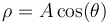
ya no es tan evidente. No es una curva sinusoidal, sino que representa otra circunferencia, pero no centrada en el origen, sino en 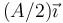 .
.
Una curva importante es de la forma
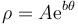
En esta curva la distancia al origen crece exponencialmente a medida que aumenta el ángulo θ. Esta curva se denomina espiral logarítmica y aparece en toda clase de fenómenos, desde la concha de los caracoles a los brazos de las galaxias espirales.
4 Coordenadas cilíndricas y esféricas
Las coordenadas polares del plano pueden extenderse a tres dimensiones de diferentes maneras. Las dos más simples son las coordenadas cilíndricas y las esféricas.
4.1 Coordenadas cilíndricas
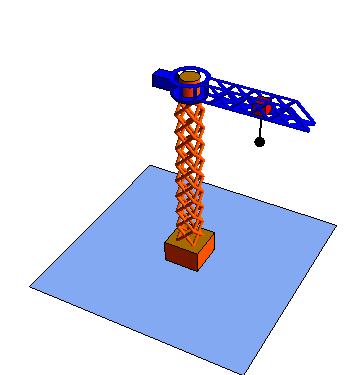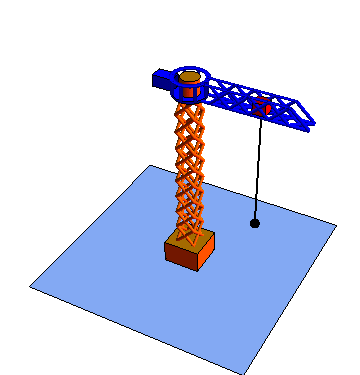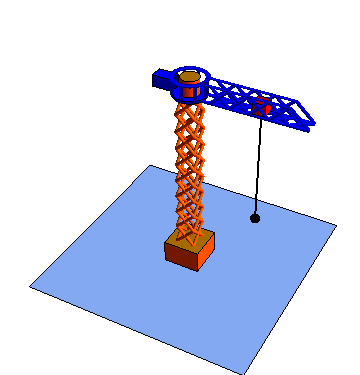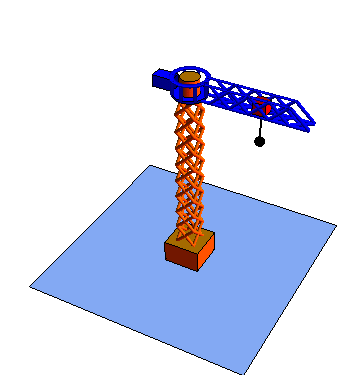
Las coordenadas polares pueden extenderse a tres dimensiones añadiendo una tercera coordenada cartesiana, que sería la altura z.
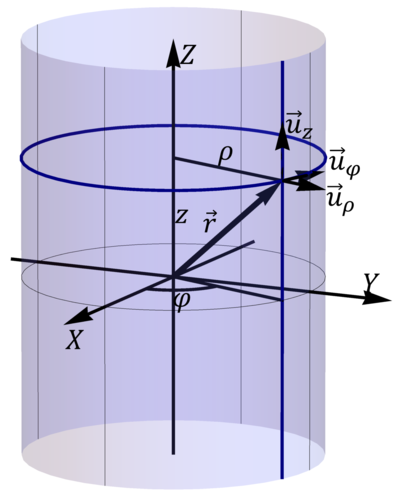
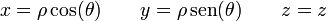
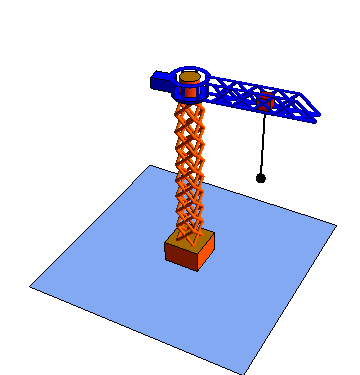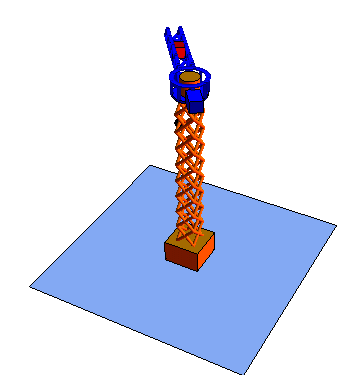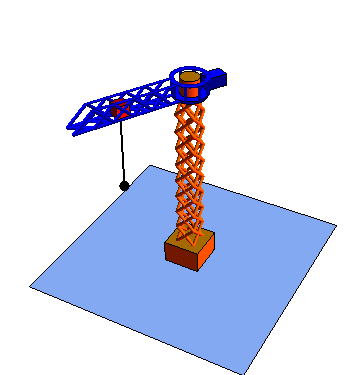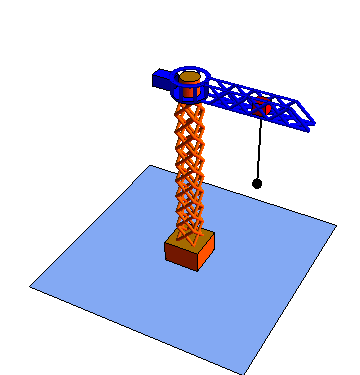
Estas tres coordenadas se denomina respectivamente radial, acimutal y vertical
| Movimiento radial | Movimiento acimutal | Movimiento vertical |
|---|---|---|
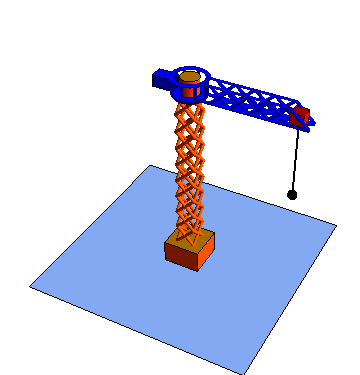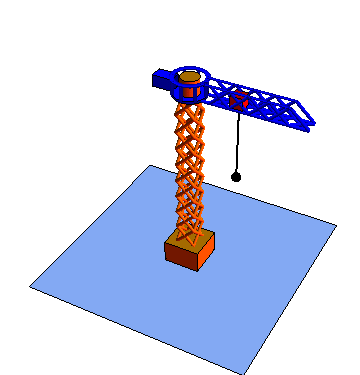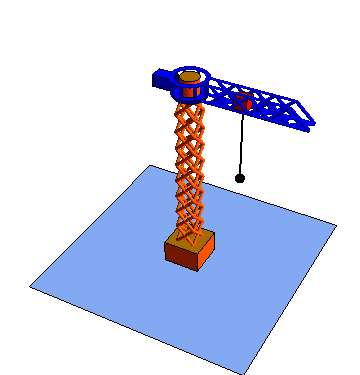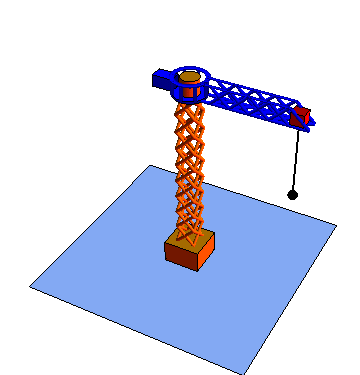
| 
| 
|
La base vectorial se amplía simplemente añadiendo el vector
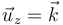
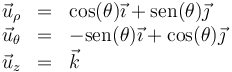
Esta base es ortonormal y dextrógira.
En coordenadas cilíndricas la posición de una partícula queda
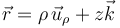
Un movimiento sencillo de representar en coordenadas cilíndricas sería el de una hélice (no confundir con una espiral), recorrida con rapidez constante
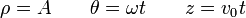
4.2 Coordenadas esféricas
Otra posible generalización consiste en convertir el plano OXY en el OXZ y girarlo alrededor del eje OZ. Añadimos entonces una tercera coordenada  que representa el giro del vector de posición alrededor del eje OZ. De esta forma, las coordenadas cartesianas de la posición se expresan
que representa el giro del vector de posición alrededor del eje OZ. De esta forma, las coordenadas cartesianas de la posición se expresan


Geométricamente,
- r, coordenada radial, varía en
 , es la distancia al origen de coordenadas
, es la distancia al origen de coordenadas
- θ, coordenada polar, varía en [0,π], es el ángulo que el vector de posición forma con el eje OZ. Esta coordenada equivale a la colatitud en la superficie terrestre, esto es, el ángulo complementario a la latitud, que es el ángulo que el vector de posición forma con el plano ecuatorial.
-
 , coordenada acimutal, varía en [0,2π], representa el ángulo forma con OX la proyección del vector de posición con el plano OXY. En la superficie terrestre equivale a la longitud respecto al meridiano de Greenwich.
, coordenada acimutal, varía en [0,2π], representa el ángulo forma con OX la proyección del vector de posición con el plano OXY. En la superficie terrestre equivale a la longitud respecto al meridiano de Greenwich.


En coordenadas esféricas, las superficies r = cte. son esferas concéntricas, las θ = cte. son conos con vértice el origen y eje el OZ y las 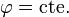 son semiplanos verticales.
son semiplanos verticales.
Existe más de una definición de las coordenadas esféricas, en particular, en muchos casos se intercambian los nombres de θ y  , por lo que hay que prestar atención a la definición en cada caso.
, por lo que hay que prestar atención a la definición en cada caso.
Las coordenadas esféricas llevan asociadas una base vectorial 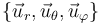 dependiente de la posición, donde cada vector es el unitario en la dirección y sentido en que aumenta cada coordenada.
dependiente de la posición, donde cada vector es el unitario en la dirección y sentido en que aumenta cada coordenada.
Si lo representamos sobre una superficie de una esfera, que podemos imaginar la terrestre, el unitario radial 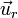 va hacia afuera de la esfera, el polar
va hacia afuera de la esfera, el polar 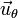 va hacia el sur y el acimutal
va hacia el sur y el acimutal 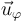 va hacia el este.
va hacia el este.
La expresión de la base de esféricas en función de la canónica es más complicada que en cilíndricas
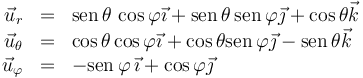
Estos vectores dependen de la posición a través de los ángulos θ y  , cumpliéndose las relaciones
, cumpliéndose las relaciones
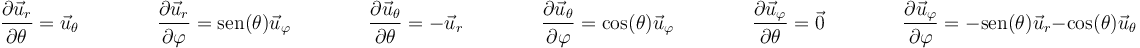
5 Ortonormalidad de las bases
La base canónica  , la asociada a cilíndricas
, la asociada a cilíndricas 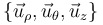 y la asociada a esféricas
y la asociada a esféricas 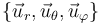 son las tres ortonormales, es decir, los vectores de cada una son unitarios, son ortogonales con los otros dos vectores de la misma base y cumplen la regla de la mano derecha en el producto vectorial (siempre que se sitúen en el orden indicado).
son las tres ortonormales, es decir, los vectores de cada una son unitarios, son ortogonales con los otros dos vectores de la misma base y cumplen la regla de la mano derecha en el producto vectorial (siempre que se sitúen en el orden indicado).
| 
| 
|
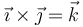
| 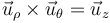
| 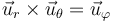
|