Velocidad y aceleración orbital de la Tierra
De Laplace
(Página creada con '==Enunciado== La órbita terrestre es aproximadamente circular con un radio 1UA = 149.60Gm. ¿Cuánto vale la rapidez y la aceleración normal de la Tierra en su movimiento orbi…') |
|||
| (Una edición intermedia no se muestra.) | |||
| Línea 3: | Línea 3: | ||
==Solución== | ==Solución== | ||
| + | El movimiento que hace la Tierra es aproximadamente circular con un periodo de 1 año. La duración en segundos es | ||
| + | |||
| + | <center><math>T = 1\,\mathrm{yr}=365.2425\,\mathrm{d}=31556952\,\mathrm{s}</math></center> | ||
| + | |||
| + | y el radio orbital medio | ||
| + | |||
| + | <center><math>R=d_{ST}=149.60\times 10^9\,\mathrm{m}</math></center> | ||
| + | |||
| + | En este movimiento, la rapidez vale | ||
| + | |||
| + | <center><math>|\vec{v}| = \omega d_{ST}= \frac{2\pi}{T}d_{ST} = \frac{2\pi}{31556952}\times 149.60\times 10^9 \,\frac{\mathrm{m}}{\mathrm{s}}=29.8\,\frac{\mathrm{km}}{\mathrm{s}}</math></center> | ||
| + | |||
| + | es decir, la Tierra se mueve a unos 30km/s por el espacio, lo cual es 60 veces más que lo que tiene el ecuador por el movimiento de rotación terrestre. | ||
| + | |||
| + | Esta gran velocidad no es apreciable en los experimentos, porque lo que influye es la aceleración. Ésta vale | ||
| + | |||
| + | <center><math>a_n= \omega^2 d_{ST}=0.00593\frac{\mathrm{m}}{\mathrm{s}^2}= 0.0006g</math></center> | ||
| + | |||
| + | es decir, en un experimento realizado sobre la superficie terrestre, la aceleración debida a la traslación solo afecta en la 5ª cifra decimal (mientras que la aceleración debida a la rotación es 5 veces mayor en influe en la 4ª cifra). | ||
| + | |||
| + | [[Categoría:Problemas de cinemática tridimensional (GIE)]] | ||
última version al 16:37 10 oct 2017
1 Enunciado
La órbita terrestre es aproximadamente circular con un radio 1UA = 149.60Gm. ¿Cuánto vale la rapidez y la aceleración normal de la Tierra en su movimiento orbital?
2 Solución
El movimiento que hace la Tierra es aproximadamente circular con un periodo de 1 año. La duración en segundos es
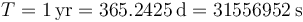
y el radio orbital medio
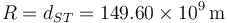
En este movimiento, la rapidez vale
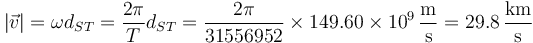
es decir, la Tierra se mueve a unos 30km/s por el espacio, lo cual es 60 veces más que lo que tiene el ecuador por el movimiento de rotación terrestre.
Esta gran velocidad no es apreciable en los experimentos, porque lo que influye es la aceleración. Ésta vale

es decir, en un experimento realizado sobre la superficie terrestre, la aceleración debida a la traslación solo afecta en la 5ª cifra decimal (mientras que la aceleración debida a la rotación es 5 veces mayor en influe en la 4ª cifra).





