Campo magnético producido por una espira rectangular
De Laplace
(Página creada con '==Enunciado== Halle el campo magnético producido por un segmento rectilíneo de corriente de longitud <math>h</math>, por el cual circula una corriente <math>I_0</math> en cual…') |
|||
| (5 ediciones intermedias no se muestran.) | |||
| Línea 4: | Línea 4: | ||
A partir del resultado anterior, hállese el campo magnético en el centro de una espira rectangular de lados <math>a</math> y <math>b</math> por la cual circula una corriente <math>I_0</math>. | A partir del resultado anterior, hállese el campo magnético en el centro de una espira rectangular de lados <math>a</math> y <math>b</math> por la cual circula una corriente <math>I_0</math>. | ||
===Campo de un segmento=== | ===Campo de un segmento=== | ||
| + | El campo magnético creado por una distribución lineal de corriente viene dado por la ley de Biot y Savart | ||
| + | |||
| + | <center><math>\vec{B}(\vec{r})=\frac{\mu_0I}{2\pi}\int_A^B\frac{\mathrm{d}\vec{r}'\times(\vec{r}-\vec{r}')}{|\vec{r}-\vec{r}'|^3}</math></center> | ||
| + | |||
| + | siendo <math>\vec{r}</math> el punto donde queremos hallar el campo y <math>\vec{r}'</math> los puntos donde se encuentran las corrientes. A y B son los puntos inicial y final de la corriente. | ||
| + | |||
| + | Obviamente, para una línea abierta, como un segmento, esto solo tiene sentido si consideramos el arco como parte de un circuito completo, ya que una corriente no puede aparecer de la nada ni desvanecerse. | ||
| + | |||
| + | En nuestro caso, situamos el segmento sobre el eje OZ (o viceversa) desde el punto <math>a\vec{k}</math> al <math>b\vec{k}</math> con lo que | ||
| + | |||
| + | <center><math>\vec{r}'=z'\vec{k}\qquad\qquad\mathrm{d}\vec{r}'=\mathrm{d}z'\vec{k}\qquad\qquad z\in(a,b)</math></center> | ||
| + | |||
| + | [[Imagen:Alfassegmento.gif|right|200px]] | ||
| + | |||
| + | El punto de observación es arbitrario. Dada la simetría del sistema alrededor del eje OZ, el campo va a depender de la distancia al eje OZ y de la altura, pero no del ángulo <math>\theta</math>. Por ello, podemos suponer en el punto en el eje OX y para otros puntos girar el de este punto. | ||
| + | |||
| + | Con estas hipótesis, la integral para el campo queda | ||
| + | |||
| + | <center><math>\vec{B}(x)=\frac{\mu_0I}{4\pi}\int_a^b\frac{(\mathrm{d}z'\vec{k})\times(x\vec{\imath}-z'\vec{k})}{(x^2+z'^2)^{3/2}}= \frac{\mu_0Ix\vec{\jmath}}{4\pi}\int_a^b\frac{\mathrm{d}z'}{(x^2+z'^2)^{3/2}}</math></center> | ||
| + | |||
| + | Esta integral se resuelve mediante el cambio de variable | ||
| + | |||
| + | <center><math>z'-z = x\,\mathrm{tg}(\alpha)</math></center> | ||
| + | |||
| + | <math>\alpha</math> es el ángulo con el que se ve un punto cualquiera del segmento desde el punto donde queremos hallar el campo. Sean <math>\alpha_1</math> y <math>\alpha_2</math> los ángulos con que se ven los extremos del segmento. | ||
| + | |||
| + | Este cambio de variable trasforma la integral en | ||
| + | |||
| + | <center><math>\vec{B}(x)=\frac{\mu_0I\vec{\jmath}}{4\pi x}\int_{\alpha_1}^{\alpha_2}\cos(\alpha)\mathrm{d}\alpha= | ||
| + | \frac{\mu _0I\vec{\jmath}}{4\pi x}\left(\mathrm{sen}\,{\alpha_2} - \,\mathrm{sen}{\alpha_1}\right)</math></center> | ||
| + | |||
| + | Estos senos pueden calcularse a partir de los datos del problema como catetos opuestos divididos por hipotenusas | ||
| + | |||
| + | <center><math>\mathrm{sen}(\alpha_2)=\frac{b}{\sqrt{b^2+x^2}}\qquad\qquad \mathrm{sen}(\alpha_1)=\frac{a}{\sqrt{a^2+x^2}}</math></center> | ||
| + | |||
| + | aunque es más cómodo dejarlo en función de los senos y calcularlos en cada problema concreto. | ||
| + | |||
| + | El resultado se generaliza de forma inmediata si pasamos a cilíndricas. El campo tendrá el mismo módulo para todos los puntos a la misma distancia al eje, y la dirección de <math>\vec{\jmath}</math> es la ortogonal al vector de posición <math>x\vec{\imath}</math>, lo que en cilíndricas corresponde a la expresión | ||
| + | |||
| + | <center><math>\vec{B}=\frac{\mu_0I\vec{u}_\theta}{4\pi \rho}\left(\mathrm{sen}\,{\alpha_2} - \,\mathrm{sen}{\alpha_1}\right)</math></center> | ||
| + | |||
| + | Si ahora queremos expresar este resultado en cartesianas observamos que | ||
| + | |||
| + | <center><math>\frac{\vec{u}_\theta}{\rho}=\frac{\rho\vec{u}_\theta}{\rho^2}=\frac{-y\vec{\imath}+x\vec{\jmath}}{x^2+y^2}</math></center> | ||
| + | |||
| + | lo que nos da el resultado | ||
| + | |||
| + | <center><math>\vec{B}=\frac{\mu_0I(-y\vec{\imath}+x\vec{\jmath})}{4\pi (x^2+y^2)}\left(\mathrm{sen}\,{\alpha_2} - \,\mathrm{sen}{\alpha_1}\right)</math></center> | ||
| + | |||
| + | De la expresión en cilíndricas se ve que las líneas de campo magnético dan vueltas en torno al eje del segmento, según la regla de la mano derecha. | ||
| + | |||
===En una posición arbitraria=== | ===En una posición arbitraria=== | ||
| + | A la hora de calcular el campo producido por ejemplo por una espira poligonal, no podemos fijar simultáneamente el eje Z sobre todos los lados a la vez, por lo que debemos reinterpretar la expresión para el campo de una forma más general. | ||
| + | |||
| + | Nuestro punto de partida es el campo magnético medido en un punto <math>P</math>, debido a un segmento rectilíneo de extremos <math>M</math> y <math>N</math>, dado por | ||
| + | |||
| + | <center><math>\vec{B}=\frac{\mu_0 I}{4\pi\rho}(\,\mathrm{sen}\,\alpha_2-\,\mathrm{sen}\,\alpha_1)\vec{n}</math></center> | ||
| + | |||
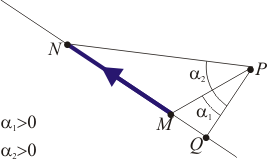
| + | [[Imagen:alfasBsegmento-1.png|left]][[Imagen:alfasBsegmento-2.png|right]]donde <math>\rho</math> debe entenderse como la distancia desde el punto donde se quiere medir el campo a la recta soporte del segmento, esto es, la distancia PQ medida sobre la perpendicular, siendo Q el punto de la recta más cercano a P. Q no tiene por qué pertenecer al segmento. <math>\alpha_1</math> y <math>\alpha_2</math> son los ángulos que esta perpendicular PQ forma con las líneas PM y PN. Estos ángulos tienen signo, positivo si PM queda por delante de PQ (según el sentido de la corriente) y negativo si queda por detrás. Lo mismo para el ángulo <math>\alpha_1</math>. Por último, <math>\vec{n}</math> representa un vector normal al plano definido por P, M y N, con sentido el dado por la regla de la mano derecha respecto a la corriente que circula por el segmento (irá hacia afuera de la pantalla si P se encuentra a la izquierda del segmento y hacia adentro si está a la derecha). | ||
| + | |||
===Campo en el centro de una espira rectangular=== | ===Campo en el centro de una espira rectangular=== | ||
| + | Una espira rectangular puede verse como una superposición de cuatro segmentos rectilíneos. | ||
| + | |||
| + | Situamos la espira en el plano OXY, con el origen en el centro del rectángulo y los ejes paralelos a los lados. Suponemos el sentido de recorrido como antihorario alrededor del eje OZ. | ||
| + | |||
| + | En este caso, la aplicación de la fórmula anterior da, para los cuatro lados, que el campo va en el sentido del eje OZ positivo, por lo que simplemente hay que sumar la magnitud de cada uno. | ||
===Campo en el centro de un polígono=== | ===Campo en el centro de un polígono=== | ||
[[Categoría:Problemas de campo magnético (GIE)]] | [[Categoría:Problemas de campo magnético (GIE)]] | ||
última version al 09:14 9 jun 2017
Contenido |
1 Enunciado
Halle el campo magnético producido por un segmento rectilíneo de corriente de longitud h, por el cual circula una corriente I0 en cualquier punto del espacio. Para fijar ideas, sitúese el eje OZ sobre el segmento, extendiéndose éste desde 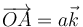 a
a 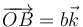 (b > a) con la corriente de A a B, y hállese el campo en un punto
(b > a) con la corriente de A a B, y hállese el campo en un punto 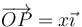 . Posteriormente generalícese el resultado.
. Posteriormente generalícese el resultado.
A partir del resultado anterior, hállese el campo magnético en el centro de una espira rectangular de lados a y b por la cual circula una corriente I0.
1.1 Campo de un segmento
El campo magnético creado por una distribución lineal de corriente viene dado por la ley de Biot y Savart
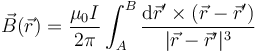
siendo  el punto donde queremos hallar el campo y
el punto donde queremos hallar el campo y 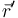 los puntos donde se encuentran las corrientes. A y B son los puntos inicial y final de la corriente.
los puntos donde se encuentran las corrientes. A y B son los puntos inicial y final de la corriente.
Obviamente, para una línea abierta, como un segmento, esto solo tiene sentido si consideramos el arco como parte de un circuito completo, ya que una corriente no puede aparecer de la nada ni desvanecerse.
En nuestro caso, situamos el segmento sobre el eje OZ (o viceversa) desde el punto 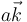 al
al 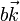 con lo que
con lo que
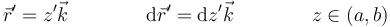
El punto de observación es arbitrario. Dada la simetría del sistema alrededor del eje OZ, el campo va a depender de la distancia al eje OZ y de la altura, pero no del ángulo θ. Por ello, podemos suponer en el punto en el eje OX y para otros puntos girar el de este punto.
Con estas hipótesis, la integral para el campo queda
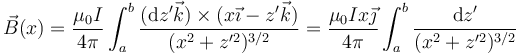
Esta integral se resuelve mediante el cambio de variable
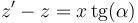
α es el ángulo con el que se ve un punto cualquiera del segmento desde el punto donde queremos hallar el campo. Sean α1 y α2 los ángulos con que se ven los extremos del segmento.
Este cambio de variable trasforma la integral en
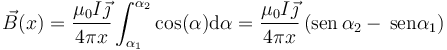
Estos senos pueden calcularse a partir de los datos del problema como catetos opuestos divididos por hipotenusas

aunque es más cómodo dejarlo en función de los senos y calcularlos en cada problema concreto.
El resultado se generaliza de forma inmediata si pasamos a cilíndricas. El campo tendrá el mismo módulo para todos los puntos a la misma distancia al eje, y la dirección de  es la ortogonal al vector de posición
es la ortogonal al vector de posición 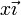 , lo que en cilíndricas corresponde a la expresión
, lo que en cilíndricas corresponde a la expresión
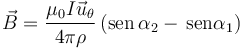
Si ahora queremos expresar este resultado en cartesianas observamos que

lo que nos da el resultado
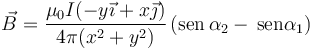
De la expresión en cilíndricas se ve que las líneas de campo magnético dan vueltas en torno al eje del segmento, según la regla de la mano derecha.
1.2 En una posición arbitraria
A la hora de calcular el campo producido por ejemplo por una espira poligonal, no podemos fijar simultáneamente el eje Z sobre todos los lados a la vez, por lo que debemos reinterpretar la expresión para el campo de una forma más general.
Nuestro punto de partida es el campo magnético medido en un punto P, debido a un segmento rectilíneo de extremos M y N, dado por
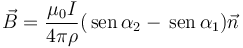
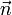 representa un vector normal al plano definido por P, M y N, con sentido el dado por la regla de la mano derecha respecto a la corriente que circula por el segmento (irá hacia afuera de la pantalla si P se encuentra a la izquierda del segmento y hacia adentro si está a la derecha).
representa un vector normal al plano definido por P, M y N, con sentido el dado por la regla de la mano derecha respecto a la corriente que circula por el segmento (irá hacia afuera de la pantalla si P se encuentra a la izquierda del segmento y hacia adentro si está a la derecha).
1.3 Campo en el centro de una espira rectangular
Una espira rectangular puede verse como una superposición de cuatro segmentos rectilíneos.
Situamos la espira en el plano OXY, con el origen en el centro del rectángulo y los ejes paralelos a los lados. Suponemos el sentido de recorrido como antihorario alrededor del eje OZ.
En este caso, la aplicación de la fórmula anterior da, para los cuatro lados, que el campo va en el sentido del eje OZ positivo, por lo que simplemente hay que sumar la magnitud de cada uno.