Dipolo eléctrico (GIE)
De Laplace
(→Campo eléctrico) |
|||
| (18 ediciones intermedias no se muestran.) | |||
| Línea 7: | Línea 7: | ||
<center>[[Archivo:dipolo-agua.jpg|500px]]</center> | <center>[[Archivo:dipolo-agua.jpg|500px]]</center> | ||
| - | No todas las moléculas poseen momento dipolar. El dióxido de carbono, por ejemplo, es una | + | No todas las moléculas poseen momento dipolar. El dióxido de carbono, por ejemplo, es una molécula simétrica que no tiene momento dipolar neto ya que el centro de las cargas positivas y el de las cargas negativas es el mismo. |
El dipolo se caracteriza matemáticamente por su ''momento dipolar'', que para dos cargas puntuales se define como | El dipolo se caracteriza matemáticamente por su ''momento dipolar'', que para dos cargas puntuales se define como | ||
| Línea 17: | Línea 17: | ||
Esta expresión se generaliza fácilmente a una distribución arbitraria observando que equivale a | Esta expresión se generaliza fácilmente a una distribución arbitraria observando que equivale a | ||
| - | <center><math>\vec{p}=q(\vec{r}_{+}-\vec{r}_{-})=q_{+}\vec{r}_{+}+q_{-}\vec{r}_{-}</math></center> | + | <center><math>\vec{p}=q(\vec{r}_{+}-\vec{r}_{-})=(+q)\vec{r}_{+}+(-q)\vec{r}_{-})=q_{+}\vec{r}_{+}+q_{-}\vec{r}_{-}</math></center> |
| - | Y de aquí pasamos a una distribución de cargas puntuales | + | Y de aquí pasamos a una distribución de cargas puntuales |
<center><math>\vec{p}=\sum_iq_i\vec{r}_i</math></center> | <center><math>\vec{p}=\sum_iq_i\vec{r}_i</math></center> | ||
| - | y a una | + | y a una distribución volumétrica, superficial o lineal |
| + | |||
| + | <center><math>\vec{p}=\int_Q \vec{r}\,\mathrm{d}q</math></center> | ||
| + | |||
| + | El momento dipolar es una magnitud vectorial cuya unidad en el SI es el culombio·metro. | ||
| - | |||
==Efecto de un campo externo uniforme sobre un dipolo== | ==Efecto de un campo externo uniforme sobre un dipolo== | ||
| + | Si un dipolo se encuentra inmerso en un campo eléctrico uniforme, <math>\vec{E}_0</math>, aparecen sobre él dos fuerzas: una sobre la carga positiva y otra sobre la negativa (más si hay más de dos cargas, como en el caso del agua). | ||
| + | |||
| + | Por ser nula la carga neta se anula la resultante de las fuerzas externas sobre el dipolo | ||
| + | |||
| + | <center><math>\vec{F}=\vec{F}_++\vec{F}_- = (+q)\vec{E}_0+(-q)\vec{E}_0=(q-q)\vec{E}_0=\vec{0}</math></center> | ||
| + | |||
| + | Esto implica que, tal como se ve al estudiar la dinámica del sólido rígido, el CM del dipolo no tiende a moverse. | ||
| + | |||
| + | Sin embargo, sí que aparece un par de fuerzas, ya que las fuerzas no están aplicadas sobre la misma recta soporte. El momento del par vale | ||
| + | |||
| + | <center><math>\vec{M}=\vec{r}_+\times\vec{F}_++\vec{r}_-\times\vec{F}_-=q(\vec{r}_+-\vec{r}_-)\times\vec{E}_0=\vec{p}\times\vec{E}_0</math></center> | ||
| + | |||
| + | Esta expresión se verifica también para distribuciones dipolares más complejas, como la de la molécula de agua. Para todas ellas | ||
| + | |||
| + | <center><math>\vec{M}=\vec{p}\times\vec{E}_0</math></center> | ||
| + | |||
| + | El efecto de este par de fuerzas es girar el dipolo tendiendo a alinearlo con el campo eléctrico. Es el mismo principio que, en el campo magnético, explica el funcionamiento de una brújula. | ||
| + | |||
| + | <center>[[Archivo:par-dipolo-2.png|300px]]</center> | ||
| + | |||
==Potencial y campo debido a un dipolo== | ==Potencial y campo debido a un dipolo== | ||
| + | Un dipolo, además de experimentar los efectos de un campo externo, también genera un campo propio. | ||
| + | |||
| + | ===Potencial eléctrico=== | ||
| + | Supongamos un dipolo formado por dos cargas puntuales separadas una distancia <math>b</math>. El potencial eléctrico, en un punto <math>\vec{r}</math> del espacio, debido a estas dos cargas será | ||
| + | |||
| + | <center><math>V(\vec{r})=\frac{1}{4\pi\varepsilon_0}\left(\frac{q_+}{d_+}+\frac{q_-}{d_-}\right)</math></center> | ||
| + | |||
| + | siendo <math>d_+</math> y <math>d_-</math> las distancias a cada carga. Si sumamos las fracciones queda | ||
| + | |||
| + | <center><math>V=\frac{q}{4\pi\varepsilon_0}\,\frac{(d_--d_+)}{d_+d_-}</math></center> | ||
| + | |||
| + | En la mayoría de las situaciones, el potencial y el campo del dipolo interesan a grandes distancias de éstos (comparadas con el tamaño del propio dipolo). Por ejemplo, una molécula de agua mide unos cuantos nanómetros. Una distancia de solo 1mm ya es un millón de veces más grande que el tamaño del dipolo. | ||
| + | |||
| + | <center>[[Archivo:distancia-dipolo.png|400px]]</center> | ||
| + | |||
| + | En ese caso, podemos hacer la aproximación | ||
| + | |||
| + | <center><math>d_--d_+ \simeq b\,\cos(\theta)</math></center> | ||
| + | |||
| + | siendo <math>\theta</math> el ángulo que el vector de posición forma con el momento dipolar. Por otro lado, para distancias muy grandes | ||
| + | |||
| + | <center><math>d_+\simeq d_-\simeq r = \left|\vec{r}\right|</math></center> | ||
| + | |||
| + | lo que nos permite reducir la expresión anterior a | ||
| + | |||
| + | <center><math>V = \frac{qb\cos(\theta)}{4\pi\varepsilon_0 r^2}=\frac{p\cos(\theta)}{4\pi\varepsilon_0 r^2}</math></center> | ||
| + | |||
| + | Esta expresión nos dice que el potencial de un dipolo, a diferencia del de una carga puntual, depende de la dirección de observación (a través del ángulo <math>\theta</math>). | ||
| + | |||
| + | Depende de la distancia como <math>1/r^2</math>, mientras que el de una carga puntual va como <math>1/r</math>. Esto quiere decir que el potencial (y el campo) de un dipolo disminuyen más rápidamente con la distancia que el de la carga. Al multiplicar la distancia por 2, el potencial de una carga puntual se reduce a la mitad, pero el de un dipolo se reduce a una cuarta parte. Por ello, el efecto de un dipolo se hace imperceptible a cortas distancias. La interacción entre moléculas de agua es una acción de corto alcance, que le da cohesión al agua, pero no es suficiente para unir rígidamente las moléculas. | ||
| + | |||
| + | El potencial del dipolo se puede escribir en forma vectorial con ayuda del producto escalar | ||
| + | |||
| + | <center><math>V(\vec{r})=\frac{\vec{p}\cdot\vec{u}_r}{4\pi\varepsilon_0 r^2}=\frac{\vec{p}\cdot\vec{r}}{4\pi\varepsilon_0 r^3}</math></center> | ||
| + | |||
| + | El potencial eléctrico debido a un dipolo es nulo en el plano perpendicular al momento dipolar y que pasa por el dipolo. El resto de las superficies equipotenciales son superficies cerradas de forma ovoidal. | ||
| + | |||
| + | ===Campo eléctrico=== | ||
| + | El campo eléctrico en cualquier punto del espacio puede calcularse a partir del potencial eléctrico como su gradiente cambiado de signo | ||
| + | |||
| + | <center><math>\vec{E}=-\nabla V</math></center> | ||
| + | |||
| + | En el caso del dipolo, el cálculo requiere algo de álgebra en polares, por lo que pondremos directamente el resultado | ||
| + | |||
| + | <center><math>\vec{E}=\frac{1}{4\pi\varepsilon_0}\,\frac{3(\vec{p}\cdot\vec{u}_r)\vec{u}_r-\vec{p}}{r^3}=\frac{1}{4\pi\varepsilon_0}\,\frac{3(\vec{p}\cdot\vec{r})\vec{r}-r^2\vec{p}}{r^5}</math></center> | ||
| + | |||
| + | Esta expresión nos dice que el campo eléctrico de un dipolo decae como el cubo de la distancia al dipolo. | ||
| + | |||
| + | En una gráfica log-log, resulta una recta de pendiente -3. Este decaimiento es más rápido que el de una carga puntual. Esta es la causa de que a grandes distancias el efecto de los dipolos sea despreciable frente a los de las cargas netas. Dado que el campo gravitatorio sí decae como 1/r² y la Tierra es eléctricamente neutra (con lo que será un dipolo o distribuciones que producen un campo eléctrico aun más pequeño), esto explica que a distancias astronómicas la fuerza eléctrica sea despreciable frente a la gravitatoria, pese a ser una fuerza mucho más intensa cuando hablamos de partícula a partícula. | ||
| + | |||
| + | <center>[[Archivo:campo-carga-dipolo.png]]</center> | ||
| + | |||
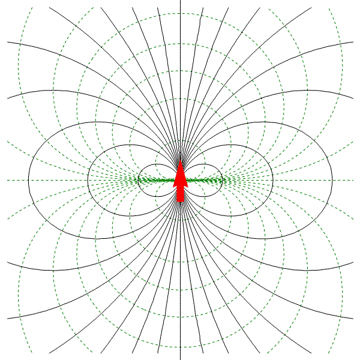
| + | La forma de las líneas de campo eléctrico son arcos casi cerrados que parten de la carga positiva y acaban en la negativa. | ||
| + | |||
| + | <center>[[Archivo:lineas-campo-dipolo.gif]]</center> | ||
[[Categoría:Electrostática en el vacío (GIE)]] | [[Categoría:Electrostática en el vacío (GIE)]] | ||
última version al 10:46 3 mar 2017
Contenido |
1 Definición. Momento dipolar
En su versión más sencilla, un dipolo es un sistema formado por dos cargas de la misma magnitud y signo opuesto, separadas una cierta distancia.

Más en general, un sistema neutro pero en el que el centro de las cargas positivas no coincide con el de las negativas también se conoce como un dipolo. Un ejemplo típico es la molécula de agua. Al ser el oxígeno más electronegativo que el hidrógeno, se produce una acumulación de carga negativa en el lado en que se halla el oxígeno, y de carga positiva en el opuesto.

No todas las moléculas poseen momento dipolar. El dióxido de carbono, por ejemplo, es una molécula simétrica que no tiene momento dipolar neto ya que el centro de las cargas positivas y el de las cargas negativas es el mismo.
El dipolo se caracteriza matemáticamente por su momento dipolar, que para dos cargas puntuales se define como
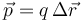
siendo 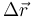 el vector de posición relativa que va de la carga negativa a la positiva.
el vector de posición relativa que va de la carga negativa a la positiva.
Esta expresión se generaliza fácilmente a una distribución arbitraria observando que equivale a
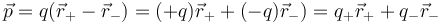
Y de aquí pasamos a una distribución de cargas puntuales
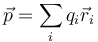
y a una distribución volumétrica, superficial o lineal
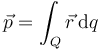
El momento dipolar es una magnitud vectorial cuya unidad en el SI es el culombio·metro.
2 Efecto de un campo externo uniforme sobre un dipolo
Si un dipolo se encuentra inmerso en un campo eléctrico uniforme, 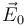 , aparecen sobre él dos fuerzas: una sobre la carga positiva y otra sobre la negativa (más si hay más de dos cargas, como en el caso del agua).
, aparecen sobre él dos fuerzas: una sobre la carga positiva y otra sobre la negativa (más si hay más de dos cargas, como en el caso del agua).
Por ser nula la carga neta se anula la resultante de las fuerzas externas sobre el dipolo
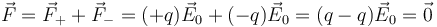
Esto implica que, tal como se ve al estudiar la dinámica del sólido rígido, el CM del dipolo no tiende a moverse.
Sin embargo, sí que aparece un par de fuerzas, ya que las fuerzas no están aplicadas sobre la misma recta soporte. El momento del par vale
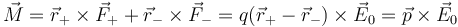
Esta expresión se verifica también para distribuciones dipolares más complejas, como la de la molécula de agua. Para todas ellas
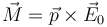
El efecto de este par de fuerzas es girar el dipolo tendiendo a alinearlo con el campo eléctrico. Es el mismo principio que, en el campo magnético, explica el funcionamiento de una brújula.

3 Potencial y campo debido a un dipolo
Un dipolo, además de experimentar los efectos de un campo externo, también genera un campo propio.
3.1 Potencial eléctrico
Supongamos un dipolo formado por dos cargas puntuales separadas una distancia b. El potencial eléctrico, en un punto  del espacio, debido a estas dos cargas será
del espacio, debido a estas dos cargas será
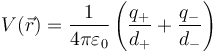
siendo d + y d − las distancias a cada carga. Si sumamos las fracciones queda
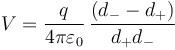
En la mayoría de las situaciones, el potencial y el campo del dipolo interesan a grandes distancias de éstos (comparadas con el tamaño del propio dipolo). Por ejemplo, una molécula de agua mide unos cuantos nanómetros. Una distancia de solo 1mm ya es un millón de veces más grande que el tamaño del dipolo.

En ese caso, podemos hacer la aproximación
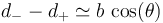
siendo θ el ángulo que el vector de posición forma con el momento dipolar. Por otro lado, para distancias muy grandes

lo que nos permite reducir la expresión anterior a
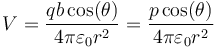
Esta expresión nos dice que el potencial de un dipolo, a diferencia del de una carga puntual, depende de la dirección de observación (a través del ángulo θ).
Depende de la distancia como 1 / r2, mientras que el de una carga puntual va como 1 / r. Esto quiere decir que el potencial (y el campo) de un dipolo disminuyen más rápidamente con la distancia que el de la carga. Al multiplicar la distancia por 2, el potencial de una carga puntual se reduce a la mitad, pero el de un dipolo se reduce a una cuarta parte. Por ello, el efecto de un dipolo se hace imperceptible a cortas distancias. La interacción entre moléculas de agua es una acción de corto alcance, que le da cohesión al agua, pero no es suficiente para unir rígidamente las moléculas.
El potencial del dipolo se puede escribir en forma vectorial con ayuda del producto escalar
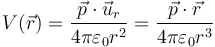
El potencial eléctrico debido a un dipolo es nulo en el plano perpendicular al momento dipolar y que pasa por el dipolo. El resto de las superficies equipotenciales son superficies cerradas de forma ovoidal.
3.2 Campo eléctrico
El campo eléctrico en cualquier punto del espacio puede calcularse a partir del potencial eléctrico como su gradiente cambiado de signo
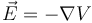
En el caso del dipolo, el cálculo requiere algo de álgebra en polares, por lo que pondremos directamente el resultado
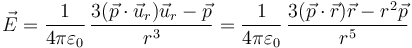
Esta expresión nos dice que el campo eléctrico de un dipolo decae como el cubo de la distancia al dipolo.
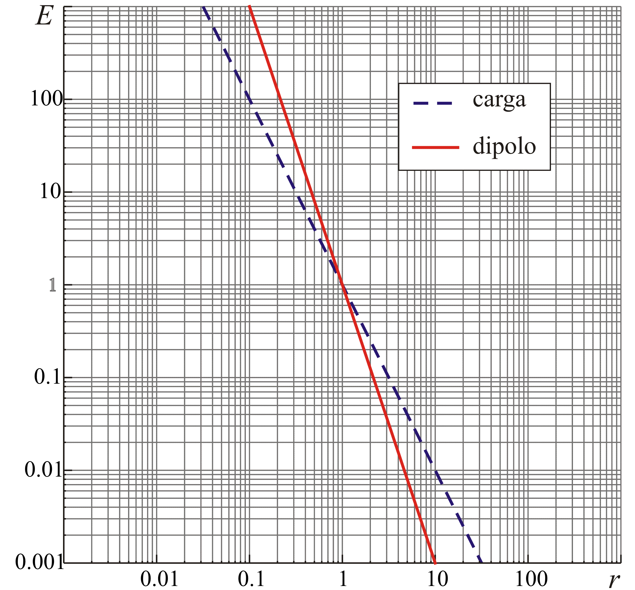
En una gráfica log-log, resulta una recta de pendiente -3. Este decaimiento es más rápido que el de una carga puntual. Esta es la causa de que a grandes distancias el efecto de los dipolos sea despreciable frente a los de las cargas netas. Dado que el campo gravitatorio sí decae como 1/r² y la Tierra es eléctricamente neutra (con lo que será un dipolo o distribuciones que producen un campo eléctrico aun más pequeño), esto explica que a distancias astronómicas la fuerza eléctrica sea despreciable frente a la gravitatoria, pese a ser una fuerza mucho más intensa cuando hablamos de partícula a partícula.
La forma de las líneas de campo eléctrico son arcos casi cerrados que parten de la carga positiva y acaban en la negativa.