Entrar Página Discusión Historial Go to the site toolbox

No Boletín - Afirmación falsa (Ex.Nov/16)

De Laplace

(Diferencias entre revisiones)
(→Solución)
(→Solución)
 
(6 ediciones intermedias no se muestran.)
Línea 17: Línea 17:
A(2,4,0)\,\,\,\longrightarrow\,\,\,\overrightarrow{OA}=2\,\vec{\imath}\,+\,4\,\vec{\jmath}\,;\,\,\,\,\,\,\,\,\,\,
A(2,4,0)\,\,\,\longrightarrow\,\,\,\overrightarrow{OA}=2\,\vec{\imath}\,+\,4\,\vec{\jmath}\,;\,\,\,\,\,\,\,\,\,\,
B(0,2,2)\,\,\,\longrightarrow\,\,\,\overrightarrow{OB}=2\,\vec{\jmath}\,+\,2\,\vec{k}\,;\,\,\,\,\,\,\,\,\,\,
B(0,2,2)\,\,\,\longrightarrow\,\,\,\overrightarrow{OB}=2\,\vec{\jmath}\,+\,2\,\vec{k}\,;\,\,\,\,\,\,\,\,\,\,
-
C(-1,0,\mathrm{p})\,\,\,\longrightarrow\,\,\,\overrightarrow{OC}=-\vec{\imath}\,+\,\mathrm{p}\,\vec{k}
+
C(-1,0,\mathrm{p})\,\,\,\longrightarrow\,\,\,\overrightarrow{OC}=-\,\vec{\imath}\,+\,\mathrm{p}\,\vec{k}
</math></center>
</math></center>
-
Y, por otra parte:
+
Y por otra parte:
<center><math>
<center><math>
-
\overrightarrow{AB}=\overrightarrow{OB}-\overrightarrow{OA}=-2\,\vec{\imath}-2\,\vec{\jmath}+2\,\vec{k}\,;\,\,\,\,\,\,\,\,\,\,\overrightarrow{BC}=\overrightarrow{OC}-\overrightarrow{OB}=-\vec{\imath}-2\,\vec{\jmath}+(\mathrm{p}-2)\,\vec{k}
+
\overrightarrow{AB}=\overrightarrow{OB}-\overrightarrow{OA}=-2\,\vec{\imath}-2\,\vec{\jmath}+2\,\vec{k}\,;\,\,\,\,\,\,\,\,\,\,\overrightarrow{BC}=\overrightarrow{OC}-\overrightarrow{OB}=-\,\vec{\imath}-2\,\vec{\jmath}+(\mathrm{p}-2)\,\vec{k}
</math></center>
</math></center>
Exigiendo la condición de ortogonalidad (producto escalar nulo) a los vectores <math>\overrightarrow{OB}\,</math> y <math>\overrightarrow{BC}\,</math>:
Exigiendo la condición de ortogonalidad (producto escalar nulo) a los vectores <math>\overrightarrow{OB}\,</math> y <math>\overrightarrow{BC}\,</math>:
<center><math>
<center><math>
-
\overrightarrow{OB}\,\cdot\,\overrightarrow{BC}=0\,\,\,\,\,\Longrightarrow\,\,\,\,\,[\,2\,\vec{\jmath}+2\,\vec{k}\,]\cdot[\,-\vec{\imath}-2\,\vec{\jmath}+(\mathrm{p}-2)\,\vec{k}\,]=0\,\,\,\,\,\Longrightarrow\,\,\,\,\,2\,\mathrm{p}-8=0\,\,\,\,\,\Longrightarrow\,\,\,\,\,\mathrm{p}=4
+
\overrightarrow{OB}\,\cdot\,\overrightarrow{BC}=0\,\,\,\,\,\Longrightarrow\,\,\,\,\,[\,2\,\vec{\jmath}\,+\,2\,\vec{k}\,]\cdot[\,-\,\vec{\imath}\,-\,2\,\vec{\jmath}\,+\,(\mathrm{p}-2)\,\vec{k}\,]=0\,\,\,\,\,\Longrightarrow\,\,\,\,\,2\,\mathrm{p}\,-\,8=0\,\,\,\,\,\Longrightarrow\,\,\,\,\,\mathrm{p}=4
</math></center>
</math></center>
Por tanto, la afirmación (2) es correcta.
Por tanto, la afirmación (2) es correcta.
Línea 31: Línea 31:
Exigiendo la condición de paralelismo (producto vectorial nulo) a los vectores <math>\overrightarrow{OA}\,</math> y <math>\overrightarrow{BC}\,</math>:
Exigiendo la condición de paralelismo (producto vectorial nulo) a los vectores <math>\overrightarrow{OA}\,</math> y <math>\overrightarrow{BC}\,</math>:
<center><math>
<center><math>
-
\overrightarrow{OA}\,\times\,\overrightarrow{BC}=\vec{0}\,\,\,\,\,\Longrightarrow\,\,\,\,\,\left|\begin{array}{ccc} \vec{\imath} & \vec{\jmath} & \vec{k} \\ 2 & 4 & 0 \\ -1 & -2 & (\mathrm{p}-2) \end{array}\right|=\vec{0}\,\,\,\,\,\Longrightarrow\,\,\,\,\,(4\,\mathrm{p}-8)\,\vec{\imath}+(-2\,\mathrm{p}+4)\,\vec{\jmath}=\vec{0}\,\,\,\,\,\Longrightarrow\,\,\,\,\,\mathrm{p}=2
+
\overrightarrow{OA}\,\times\,\overrightarrow{BC}=\vec{0}\,\,\,\,\,\Longrightarrow\,\,\,\,\,\left|\begin{array}{rrc} \vec{\imath} & \vec{\jmath} & \vec{k} \\ 2 & 4 & 0 \\ -1 & -2 & (\mathrm{p}-2) \end{array}\right|=\vec{0}\,\,\,\,\,\Longrightarrow\,\,\,\,\,(4\,\mathrm{p}\,-\,8)\,\vec{\imath}\,+\,(-2\,\mathrm{p}\,+\,4)\,\vec{\jmath}=\vec{0}\,\,\,\,\,\Longrightarrow\,\,\,\,\,\mathrm{p}=2
</math></center>
</math></center>
Por tanto, la afirmación (4) es correcta.
Por tanto, la afirmación (4) es correcta.
Línea 37: Línea 37:
Exigiendo la condición de no coplanariedad (producto mixto no nulo) a los vectores <math>\overrightarrow{OA}\,</math>, <math>\overrightarrow{OB}\,</math> y <math>\overrightarrow{OC}\,</math>, se garantiza que dicha terna constituya una base:
Exigiendo la condición de no coplanariedad (producto mixto no nulo) a los vectores <math>\overrightarrow{OA}\,</math>, <math>\overrightarrow{OB}\,</math> y <math>\overrightarrow{OC}\,</math>, se garantiza que dicha terna constituya una base:
<center><math>
<center><math>
-
\overrightarrow{OA}\cdot(\overrightarrow{OB}\times\overrightarrow{OC})\neq 0\,\,\,\,\,\Longrightarrow\,\,\,\,\,\left|\begin{array}{ccc} 2 & 4 & 0 \\ 0 & 2 & 2 \\ -1 & 0 & \mathrm{p} \end{array}\right|\neq 0\,\,\,\,\,\Longrightarrow\,\,\,\,\,4\,\mathrm{p}-8\neq 0\,\,\,\,\,\Longrightarrow\,\,\,\,\,\mathrm{p}\neq 2
+
\overrightarrow{OA}\,\cdot\,(\overrightarrow{OB}\,\times\,\overrightarrow{OC})\neq 0\,\,\,\,\,\Longrightarrow\,\,\,\,\,\left|\begin{array}{rrc} 2 & 4 & 0 \\ 0 & 2 & 2 \\ -1 & 0 & \mathrm{p} \end{array}\right|\neq 0\,\,\,\,\,\Longrightarrow\,\,\,\,\,4\,\mathrm{p}\,-\,8\neq 0\,\,\,\,\,\Longrightarrow\,\,\,\,\,\mathrm{p}\neq 2
</math></center>
</math></center>
Por tanto, la afirmación (1) es correcta.
Por tanto, la afirmación (1) es correcta.
Línea 43: Línea 43:
Por último, exigiendo la condición de coplanariedad (producto mixto nulo) a los vectores <math>\overrightarrow{OA}\,</math>, <math>\overrightarrow{AB}\,</math> y <math>\overrightarrow{BC}\,</math>:
Por último, exigiendo la condición de coplanariedad (producto mixto nulo) a los vectores <math>\overrightarrow{OA}\,</math>, <math>\overrightarrow{AB}\,</math> y <math>\overrightarrow{BC}\,</math>:
<center><math>
<center><math>
-
\overrightarrow{OA}\cdot(\overrightarrow{AB}\times\overrightarrow{BC})= 0\,\,\,\,\,\Longrightarrow\,\,\,\,\,\left|\begin{array}{ccc} 2 & 4 & 0 \\ -2 & -2 & 2 \\ -1 & -2 & (\mathrm{p}-2) \end{array}\right|=-12\,\mathrm{p}+24= 0\,\,\,\,\,\Longrightarrow\,\,\,\,\,\mathrm{p}=2
+
\overrightarrow{OA}\,\cdot\,(\overrightarrow{AB}\,\times\,\overrightarrow{BC})= 0\,\,\,\,\,\Longrightarrow\,\,\,\,\,\left|\begin{array}{rrc} 2 & 4 & 0 \\ -2 & -2 & 2 \\ -1 & -2 & (\mathrm{p}\,-\,2) \end{array}\right|=4\,\mathrm{p}\,-\,8= 0\,\,\,\,\,\Longrightarrow\,\,\,\,\,\mathrm{p}=2
</math></center>
</math></center>
Por tanto, la afirmación (3) es la que es FALSA.
Por tanto, la afirmación (3) es la que es FALSA.
[[Categoría:Problemas de vectores libres (G.I.T.I.)]]
[[Categoría:Problemas de vectores libres (G.I.T.I.)]]

última version al 22:34 1 mar 2017

1 Enunciado

En un triedro cartesiano 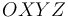OXYZ\, se consideran los siguientes puntos: 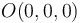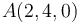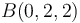O(0,0,0)\,, A(2,4,0)\,, B(0,2,2)\, y C(-1,0,p)\,.

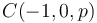¿Cuál de las siguientes afirmaciones es falsa?

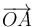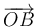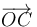(1) \overrightarrow{OA}\,, \overrightarrow{OB}\, y \overrightarrow{OC}\, constituyen una base si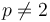 p\neq 2\,
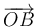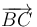(2) \overrightarrow{OB}\, y \overrightarrow{BC}\, son ortogonales si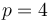 p= 4\,
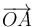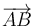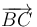(3) \overrightarrow{OA}\,, \overrightarrow{AB}\, y \overrightarrow{BC}\, son coplanarios si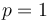 p= 1\,
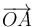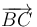(4) \overrightarrow{OA}\, y \overrightarrow{BC}\, son paralelos si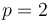 p= 2\,

2 Solución

Las coordenadas de un punto en un sistema de ejes cartesianos son las componentes de su vector de posición en la base ortonormal asociada, es decir:

A(2,4,0)\,\,\,\longrightarrow\,\,\,\overrightarrow{OA}=2\,\vec{\imath}\,+\,4\,\vec{\jmath}\,;\,\,\,\,\,\,\,\,\,\, B(0,2,2)\,\,\,\longrightarrow\,\,\,\overrightarrow{OB}=2\,\vec{\jmath}\,+\,2\,\vec{k}\,;\,\,\,\,\,\,\,\,\,\, C(-1,0,\mathrm{p})\,\,\,\longrightarrow\,\,\,\overrightarrow{OC}=-\,\vec{\imath}\,+\,\mathrm{p}\,\vec{k}

Y por otra parte:

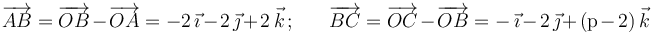
\overrightarrow{AB}=\overrightarrow{OB}-\overrightarrow{OA}=-2\,\vec{\imath}-2\,\vec{\jmath}+2\,\vec{k}\,;\,\,\,\,\,\,\,\,\,\,\overrightarrow{BC}=\overrightarrow{OC}-\overrightarrow{OB}=-\,\vec{\imath}-2\,\vec{\jmath}+(\mathrm{p}-2)\,\vec{k}

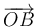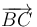Exigiendo la condición de ortogonalidad (producto escalar nulo) a los vectores \overrightarrow{OB}\, y \overrightarrow{BC}\,:

\overrightarrow{OB}\,\cdot\,\overrightarrow{BC}=0\,\,\,\,\,\Longrightarrow\,\,\,\,\,[\,2\,\vec{\jmath}\,+\,2\,\vec{k}\,]\cdot[\,-\,\vec{\imath}\,-\,2\,\vec{\jmath}\,+\,(\mathrm{p}-2)\,\vec{k}\,]=0\,\,\,\,\,\Longrightarrow\,\,\,\,\,2\,\mathrm{p}\,-\,8=0\,\,\,\,\,\Longrightarrow\,\,\,\,\,\mathrm{p}=4

Por tanto, la afirmación (2) es correcta.

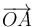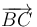Exigiendo la condición de paralelismo (producto vectorial nulo) a los vectores \overrightarrow{OA}\, y \overrightarrow{BC}\,:

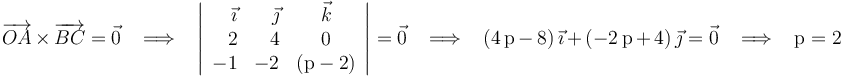
\overrightarrow{OA}\,\times\,\overrightarrow{BC}=\vec{0}\,\,\,\,\,\Longrightarrow\,\,\,\,\,\left|\begin{array}{rrc} \vec{\imath} & \vec{\jmath} & \vec{k} \\ 2 & 4 & 0 \\ -1 & -2 & (\mathrm{p}-2) \end{array}\right|=\vec{0}\,\,\,\,\,\Longrightarrow\,\,\,\,\,(4\,\mathrm{p}\,-\,8)\,\vec{\imath}\,+\,(-2\,\mathrm{p}\,+\,4)\,\vec{\jmath}=\vec{0}\,\,\,\,\,\Longrightarrow\,\,\,\,\,\mathrm{p}=2

Por tanto, la afirmación (4) es correcta.

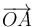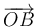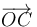Exigiendo la condición de no coplanariedad (producto mixto no nulo) a los vectores \overrightarrow{OA}\,, \overrightarrow{OB}\, y \overrightarrow{OC}\,, se garantiza que dicha terna constituya una base:

\overrightarrow{OA}\,\cdot\,(\overrightarrow{OB}\,\times\,\overrightarrow{OC})\neq 0\,\,\,\,\,\Longrightarrow\,\,\,\,\,\left|\begin{array}{rrc} 2 & 4 & 0 \\ 0 & 2 & 2 \\ -1 & 0 & \mathrm{p} \end{array}\right|\neq 0\,\,\,\,\,\Longrightarrow\,\,\,\,\,4\,\mathrm{p}\,-\,8\neq 0\,\,\,\,\,\Longrightarrow\,\,\,\,\,\mathrm{p}\neq 2

Por tanto, la afirmación (1) es correcta.

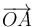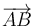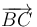Por último, exigiendo la condición de coplanariedad (producto mixto nulo) a los vectores \overrightarrow{OA}\,, \overrightarrow{AB}\, y \overrightarrow{BC}\,:

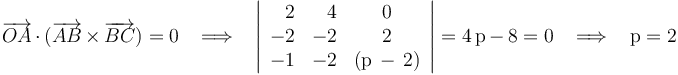
\overrightarrow{OA}\,\cdot\,(\overrightarrow{AB}\,\times\,\overrightarrow{BC})= 0\,\,\,\,\,\Longrightarrow\,\,\,\,\,\left|\begin{array}{rrc} 2 & 4 & 0 \\ -2 & -2 & 2 \\ -1 & -2 & (\mathrm{p}\,-\,2) \end{array}\right|=4\,\mathrm{p}\,-\,8= 0\,\,\,\,\,\Longrightarrow\,\,\,\,\,\mathrm{p}=2

Por tanto, la afirmación (3) es la que es FALSA.

Obtenido de "http://tesla.us.es/wiki/index.php/No_Bolet%C3%ADn_-_Afirmaci%C3%B3n_falsa_(Ex.Nov/16)"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Esta página fue modificada por última vez el 22:34, 1 mar 2017. - Esta página ha sido visitada 3.205 veces. - Aviso legal - Acerca de Laplace