No Boletín - Afirmación falsa (Ex.Nov/16)

De Laplace

(Diferencias entre revisiones)

Revisión de 21:04 1 mar 2017

1 Enunciado

En un triedro cartesiano 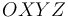$OXYZ\,$ se consideran los siguientes puntos: 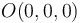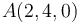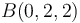$O(0,0,0)\,$ , $A(2,4,0)\,$ , $B(0,2,2)\,$ y $C(-1,0,p)\,$ .

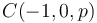¿Cuál de las siguientes afirmaciones es falsa?

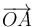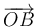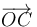(1) $\overrightarrow{OA}\,$ , $\overrightarrow{OB}\,$ y $\overrightarrow{OC}\,$ constituyen una base si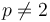 $p\neq 2\,$

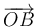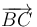(2) $\overrightarrow{OB}\,$ y $\overrightarrow{BC}\,$ son ortogonales si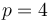 $p= 4\,$

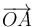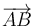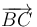(3) $\overrightarrow{OA}\,$ , $\overrightarrow{AB}\,$ y $\overrightarrow{BC}\,$ son coplanarios si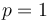 $p= 1\,$

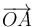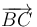(4) $\overrightarrow{OA}\,$ y $\overrightarrow{BC}\,$ son paralelos si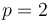 $p= 2\,$

2 Solución

Las coordenadas de un punto en un sistema de ejes cartesianos son las componentes de su vector de posición en la base ortonormal asociada, es decir:

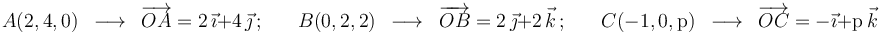
$A(2,4,0)\,\,\,\longrightarrow\,\,\,\overrightarrow{OA}=2\,\vec{\imath}+4\,\vec{\jmath}\,;\,\,\,\,\,\,\,\,\,\, B(0,2,2)\,\,\,\longrightarrow\,\,\,\overrightarrow{OB}=2\,\vec{\jmath}+2\,\vec{k}\,;\,\,\,\,\,\,\,\,\,\, C(-1,0,\mathrm{p})\,\,\,\longrightarrow\,\,\,\overrightarrow{OC}=-\vec{\imath}+\mathrm{p}\,\vec{k}$

Y, por otra parte:

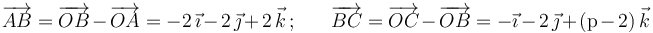
$\overrightarrow{AB}=\overrightarrow{OB}-\overrightarrow{OA}=-2\,\vec{\imath}-2\,\vec{\jmath}+2\,\vec{k}\,;\,\,\,\,\,\,\,\,\,\,\overrightarrow{BC}=\overrightarrow{OC}-\overrightarrow{OB}=-\vec{\imath}-2\,\vec{\jmath}+(\mathrm{p}-2)\,\vec{k}$

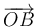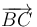Exigiendo la condición de ortogonalidad (producto escalar nulo) a los vectores $\overrightarrow{OB}\,$ y $\overrightarrow{BC}\,$ :

$\overrightarrow{OB}\cdot\overrightarrow{BC}=0\,\,\,\,\,\Longrightarrow\,\,\,\,\,[2\,\vec{\jmath}+2\,\vec{k}]\cdot[-\vec{\imath}-2\,\vec{\jmath}+(\mathrm{p}-2)\,\vec{k}]=0\,\,\,\,\,\Longrightarrow\,\,\,\,\,2\,\mathrm{p}-8=0\,\,\,\,\,\Longrightarrow\,\,\,\,\,\mathrm{p}=4$

Por tanto, la afirmación (2) es correcta.

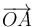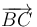Exigiendo la condición de paralelismo (producto vectorial nulo) a los vectores $\overrightarrow{OA}\,$ y $\overrightarrow{BC}\,$ :

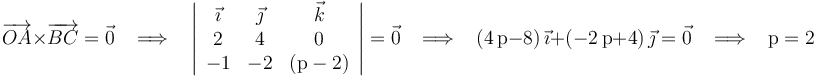
$\overrightarrow{OA}\times\overrightarrow{BC}=\vec{0}\,\,\,\,\,\Longrightarrow\,\,\,\,\,\left|\begin{array}{ccc} \vec{\imath} & \vec{\jmath} & \vec{k} \\ 2 & 4 & 0 \\ -1 & -2 & (\mathrm{p}-2) \end{array}\right|=\vec{0}\,\,\,\,\,\Longrightarrow\,\,\,\,\,(4\,\mathrm{p}-8)\,\vec{\imath}+(-2\,\mathrm{p}+4)\,\vec{\jmath}=\vec{0}\,\,\,\,\,\Longrightarrow\,\,\,\,\,\mathrm{p}=2$

Por tanto, la afirmación (4) es correcta.

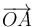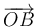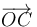Exigiendo la condición de no coplanariedad (producto mixto no nulo) a los vectores $\overrightarrow{OA}\,$ , $\overrightarrow{OB}\,$ y $\overrightarrow{OC}\,$ , se garantiza que dicha terna constituya una base:

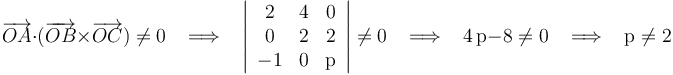
$\overrightarrow{OA}\cdot(\overrightarrow{OB}\times\overrightarrow{OC})\neq 0\,\,\,\,\,\Longrightarrow\,\,\,\,\,\left|\begin{array}{ccc} 2 & 4 & 0 \\ 0 & 2 & 2 \\ -1 & 0 & \mathrm{p} \end{array}\right|\neq 0\,\,\,\,\,\Longrightarrow\,\,\,\,\,4\,\mathrm{p}-8\neq 0\,\,\,\,\,\Longrightarrow\,\,\,\,\,\mathrm{p}\neq 2$

Por tanto, la afirmación (1) es correcta.

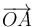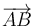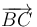Por último, exigiendo la condición de coplanariedad (producto mixto nulo) a los vectores $\overrightarrow{OA}\,$ , $\overrightarrow{AB}\,$ y $\overrightarrow{BC}\,$ :

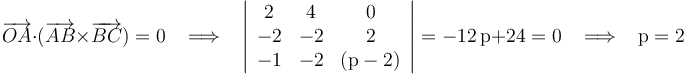
$\overrightarrow{OA}\cdot(\overrightarrow{AB}\times\overrightarrow{BC})= 0\,\,\,\,\,\Longrightarrow\,\,\,\,\,\left|\begin{array}{ccc} 2 & 4 & 0 \\ -2 & -2 & 2 \\ -1 & -2 & (\mathrm{p}-2) \end{array}\right|=-12\,\mathrm{p}+24= 0\,\,\,\,\,\Longrightarrow\,\,\,\,\,\mathrm{p}=2$

Por tanto, la afirmación (3) es la que es FALSA.

@@ Línea 21: / Línea 21: @@
 Y, por otra parte:
 <center><math>
-\overrightarrow{AB}=\overrightarrow{OB}-\overrightarrow{OA}=(-2\,\vec{\imath}-2\,\vec{\jmath}+2\,\vec{k}\,;\,\,\,\,\,\,\,\,\,\,\overrightarrow{BC}=\overrightarrow{OC}-\overrightarrow{OB}=-\vec{\imath}-2\,\vec{\jmath}+(\mathrm{p}-2)\,\vec{k}
+\overrightarrow{AB}=\overrightarrow{OB}-\overrightarrow{OA}=-2\,\vec{\imath}-2\,\vec{\jmath}+2\,\vec{k}\,;\,\,\,\,\,\,\,\,\,\,\overrightarrow{BC}=\overrightarrow{OC}-\overrightarrow{OB}=-\vec{\imath}-2\,\vec{\jmath}+(\mathrm{p}-2)\,\vec{k}
 </math></center>
 Exigiendo la condición de ortogonalidad (producto escalar nulo) a los vectores <math>\overrightarrow{OB}\,</math> y <math>\overrightarrow{BC}\,</math>:

No Boletín - Afirmación falsa (Ex.Nov/16)

De Laplace

Revisión de 21:04 1 mar 2017

1 Enunciado

2 Solución

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES