Barra oscilante sometida a una percusión horizontal
De Laplace
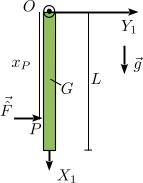
(Página creada con '== Enunciado == right Una barra homogénea de longitud <math>L</math> está articulada en un punto fijo <math>O</math> de modo que pue…') |
|||
| Línea 1: | Línea 1: | ||
| - | + | = Enunciado = | |
[[Imagen:Percusiones_barra_enunciado.jpg|right]] | [[Imagen:Percusiones_barra_enunciado.jpg|right]] | ||
Una barra homogénea de longitud <math>L</math> está articulada en un punto fijo <math>O</math> de modo que puede colgar libremente, sometida a la acción de la gravedad. En el instante inicial se encuentra en reposo y colgando verticalmente. Se aplica un percusión horizontal hacia la derecha a una distancia <math>x_P</math> del punto <math>O</math>. Determina la velocidad angular de la barra justo después de la percusión y las percusiones vinculares. Hazlo usando las herramientas de la Dinámica Vectorial y la Analítica. | Una barra homogénea de longitud <math>L</math> está articulada en un punto fijo <math>O</math> de modo que puede colgar libremente, sometida a la acción de la gravedad. En el instante inicial se encuentra en reposo y colgando verticalmente. Se aplica un percusión horizontal hacia la derecha a una distancia <math>x_P</math> del punto <math>O</math>. Determina la velocidad angular de la barra justo después de la percusión y las percusiones vinculares. Hazlo usando las herramientas de la Dinámica Vectorial y la Analítica. | ||
| - | + | = Solución = | |
| - | + | == Cinemática == | |
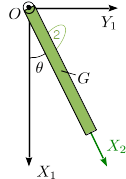
[[Archivo:Percusiones_barra_cinematica.png|right]] | [[Archivo:Percusiones_barra_cinematica.png|right]] | ||
Resolvemos primero la cinemática del problema para poder describir el movimiento. Tenemos | Resolvemos primero la cinemática del problema para poder describir el movimiento. Tenemos | ||
| Línea 17: | Línea 17: | ||
Tenemos un grado de libertad, la coordenada <math>\theta</math>. | Tenemos un grado de libertad, la coordenada <math>\theta</math>. | ||
| - | + | == Dinámica vectorial == | |
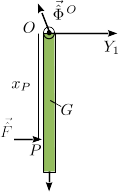
[[Archivo:Percusiones_barra_desvinculacion.png|right]] | [[Archivo:Percusiones_barra_desvinculacion.png|right]] | ||
El vínculo en el punto <math>O</math> es que ese punto no se mueve. Al ser el problema plano, implica que hay dos componentes de percusión vincular que pueden ser no nulas. Las percusiones que actúan sobre la barra son | El vínculo en el punto <math>O</math> es que ese punto no se mueve. Al ser el problema plano, implica que hay dos componentes de percusión vincular que pueden ser no nulas. Las percusiones que actúan sobre la barra son | ||
| Línea 28: | Línea 28: | ||
</math> | </math> | ||
</center> | </center> | ||
| - | Tenemos tres incógnitas: <math>\{\theta,\,\hat{O}_x,\,\hat{O}_y\}</math>. | + | Tenemos tres incógnitas: <math>\{\theta,\,\hat{O}_x,\,\hat{O}_y\}</math>. |
Tenemos que aplicar el T.C.M. impulsivo y el T.M.C. impulsivo. | Tenemos que aplicar el T.C.M. impulsivo y el T.M.C. impulsivo. | ||
| - | + | === T.C.M. === | |
Tenemos | Tenemos | ||
<center> | <center> | ||
| Línea 60: | Línea 60: | ||
<center> | <center> | ||
<math> | <math> | ||
| - | \begin{array}{ | + | \begin{array}{lclr} |
| - | (X_1) & \to & 0 = \hat{O}_x,\\ | + | (X_1) & \to & 0 = \hat{O}_x, & \qquad (1)\\ |
| - | (Y_1) & \to & \dfrac{1}{2}mL\dot{\theta}^+ = \hat{F}_0 + \hat{O}_y. | + | (Y_1) & \to & \dfrac{1}{2}mL\dot{\theta}^+ = \hat{F}_0 + \hat{O}_y. & \qquad (2) |
\end{array} | \end{array} | ||
</math> | </math> | ||
</center> | </center> | ||
| + | === T.M.C. === | ||
| + | Calculamos el momento cinético respecto del punto fijo <math>O</math>. La percusión vincular no ejerce momento respecto a este punto, por el T.C.M. impulsivo queda | ||
| + | <center> | ||
| + | <math> | ||
| + | \Delta\vec{L}_O = \overrightarrow{OP}\times\vec{\hat{F}}. | ||
| + | </math> | ||
| + | </center> | ||
| + | El momento cinético es | ||
| + | <center> | ||
| + | <math> | ||
| + | \vec{L}_O = I\vec{\omega}_{21} = I\dot{\theta}\,\vec{k}_1, | ||
| + | </math> | ||
| + | </center> | ||
| + | siendo el momento de inercia <math>I = mL^2/3</math>. El cambio en el momento de inercia durante la percusión es | ||
| + | <center> | ||
| + | <math> | ||
| + | \Delta\vec{L}_O = I(\dot{\theta}^+ -\dot{\theta}^-)\,\vec{k}_1 = | ||
| + | I\dot{\theta}^+\,\vec{k}_1. | ||
| + | </math> | ||
| + | </center> | ||
| + | El momento percusivo es | ||
| + | <center> | ||
| + | <math> | ||
| + | \overrightarrow{OP}\times\vec{\hat{F}} = | ||
| + | (x_P\vec{\imath}_1)\times(\hat{F}_0\,\vec{\jmath}_1) = | ||
| + | x_P\hat{F}_0\,\vec{k}_1. | ||
| + | </math> | ||
| + | </center> | ||
| + | La ecuación que obtenemos de aplicar el T.M.C. impulsivo es | ||
| + | <center> | ||
| + | <math> | ||
| + | \begin{array}{lr} | ||
| + | I\dot{\theta}^+ = x_p\hat{F}_0 & \qquad (3). | ||
| + | \end{array} | ||
| + | </math> | ||
| + | </center> | ||
| + | Resolviendo las tres ecuaciones obtenemos | ||
| + | <center> | ||
| + | <math> | ||
| + | \begin{array}{l} | ||
| + | \dot{\theta}^+ = \dfrac{x_P\hat{F}_0}{I} = \dfrac{3x_p\hat{F}_0}{mL^2},\\ | ||
| + | \\ | ||
| + | \vec{\hat{\Phi}}_O = -\hat{F}_0\left(1-\dfrac{3x_P}{2L}\right)\,\vec{\jmath}_1. | ||
| + | \end{array} | ||
| + | </math> | ||
| + | </center> | ||
| + | Vemos que si <math>x_P= 2L/3</math>, la percusión vincular se anula. Si esto ocurre, la velocidad del punto <math>O</math> es nula durante la percusión, y no hace falta que el vínculo actúa. Se dice entonces que el punto <math>O</math> es el centro de percusión del punto <math>P</math>. | ||
| + | |||
| + | === Evolución posterior=== | ||
| + | Después de la percusión el movimiento de la barra se describe con los teoremas habituales (T.C.M., T.M.C. y energía). El resultado de la percusión se usa como condiciones iniciales de las ecuaciones obtenidas al aplicar los teoremas. En este caso las condiciones iniciales serían | ||
| + | <center> | ||
| + | <math> | ||
| + | \theta(0)=0\, \qquad\qquad \dot{\theta}(0)=\dot{\theta}^+ = \dfrac{3x_P\hat{F}_0}{mL^2}. | ||
| + | </math> | ||
| + | </center> | ||
| + | |||
| + | == Dinámica analítica == | ||
| + | El problema tiene un grado de libertad. Elegimos la coordenada generalizada <math>\{\theta\}</math> para describirlo. La energía cinética es, usando que el punto <math>O</math> es un punto fijo | ||
| + | <center> | ||
| + | <math> | ||
| + | T = \dfrac{1}{2}I|\vec{\omega}_{21}|^2 = \dfrac{1}{2}I\dot{\theta}^2. | ||
| + | </math> | ||
| + | </center> | ||
| + | Para la energía potencial gravitatoria elegimos como origen de potencial la altura del eje <math>Y_1</math>. Entonces | ||
| + | <center> | ||
| + | <math> | ||
| + | U = - \dfrac{1}{2}mgL\cos\theta. | ||
| + | </math> | ||
| + | </center> | ||
| + | La Lagrangiana es | ||
| + | <center> | ||
| + | <math> | ||
| + | L = T - U | ||
| + | = | ||
| + | \dfrac{1}{2}I\dot{\theta}^2 + \dfrac{1}{2}mgL\cos\theta. | ||
| + | </math> | ||
| + | </center> | ||
| + | La ecuación de Lagrange impulsiva es | ||
| + | <center> | ||
| + | <math> | ||
| + | \Delta p_{\theta} = \hat{Q}^{NC}_{\theta}. | ||
| + | </math> | ||
| + | </center> | ||
| + | El momento generalizado es | ||
| + | <center> | ||
| + | <math> | ||
| + | p_{\theta} = \dfrac{\partial L}{\partial \dot{\theta}} = I\dot{\theta}. | ||
| + | </math> | ||
| + | </center> | ||
| + | El cambio durante la percusión es | ||
| + | <center> | ||
| + | <math> | ||
| + | \Delta p_{\theta} = I(\dot{\theta}^+-\dot{\theta}^-) = I\dot{\theta}^+. | ||
| + | </math> | ||
| + | </center> | ||
| + | La percusión generalizada es | ||
| + | <center> | ||
| + | <math> | ||
| + | \hat{Q}^{NC}_{\theta} = \vec{\hat{F}}\cdot\dfrac{\partial\vec{v}^{\,P}_{21}}{\partial\dot{\theta}}. | ||
| + | </math> | ||
| + | </center> | ||
| + | La velocidad es | ||
| + | <center> | ||
| + | <math> | ||
| + | \vec{v}^{\,P}_{21} = \vec{v}^{\,O}_{21} + \vec{\omega}_{21}\times\overrightarrow{OP}= | ||
| + | (\dot{\theta})\,\vec{k}_1)\times(x_P\,\vec{\imath}_1) = x_P\dot{\theta}\,\vec{\jmath}_1. | ||
| + | </math> | ||
| + | </center> | ||
| + | La percusión generalizada es | ||
| + | <center> | ||
| + | <math> | ||
| + | \vec{Q}^{NC}_{\theta} = \hat{F}_0x_P, | ||
| + | </math> | ||
| + | </center> | ||
| + | y la ecuación de Lagrange impulsiva queda | ||
| + | <center> | ||
| + | <math> | ||
| + | \dot{\theta}^+ = \dfrac{x_P\hat{F}_0}{I} = \dfrac{3x_P\hat{F}_0}{mL^2}. | ||
| + | </math> | ||
| + | </center> | ||
| + | No obtenemos las percusiones vinculares pues no aparecen en la formulación analítica. | ||
| + | === Calculo de percusiones vinculares con Dinámica analítica === | ||
| + | Pueden calcularse las percusiones vinculares con las herramientas de la Dinámica analítica usando el Principio de Liberación o los Multiplicadores de Lagrange. Vamos a calcular la reacción percusiva horizontal en el punto <math>O</math>. Liberamos la restricción <math>y=0</math> para el punto <math>O</math>. Tenemos entonces dos grados de libertad y dos coordenadas generalizadas: <math>\{\theta,\, y_O\}</math>. Al liberar el vínculo, debemos introducir una percusión | ||
| + | <center> | ||
| + | <math> | ||
| + | \vec{\hat{O}}_y = \hat{O}_y\,\vec{\jmath}_1 | ||
| + | </math> | ||
| + | </center> | ||
| + | aplicada en el punto <math>O</math>. | ||
| + | |||
| + | Ahora la reducción cinemática en el punto <math>O</math> es | ||
| + | <center> | ||
| + | <math> | ||
| + | \vec{\omega}_{21} = \dot{\theta}\,\vec{k}_1, | ||
| + | \qquad\qquad | ||
| + | \vec{v}^{\,O}_{21} = \dot{y}_O\,\vec{\jmath}_1. | ||
| + | </math> | ||
| + | </center> | ||
| + | La velocidad del centro de masas de la barra es | ||
| + | <center> | ||
| + | <math> | ||
| + | \vec{v}^{\,G}_{21} = \vec{v}^{\,O}_{21} + \vec{\omega}_{21}\times\overrightarrow{OG} = -\dfrac{1}{2}L\dot{\theta}\,\mathrm{sen}\,\theta\,\vec{\imath}_1 + \left(\dot{y}_O + \dfrac{1}{2}L\dot{\theta}\cos\theta\right)\,\vec{\jmath}_1. | ||
| + | </math> | ||
| + | </center> | ||
| + | La energía cinética de la barra es | ||
| + | <center> | ||
| + | <math> | ||
| + | T = \dfrac{1}{2}m|\vec{v}^{\,G}_{21}|^2 + \dfrac{1}{2}I_G|\vec{\omega}_{21}|^2. | ||
| + | </math> | ||
| + | </center> | ||
| + | El momento de inercia es <math>I_G = mL^2/12</math>, pues es respecto al centro de masas. Tenemos | ||
| + | <center> | ||
| + | <math> | ||
| + | T = \dfrac{1}{2}m\,\left( | ||
| + | \dot{y}_O^2 + \dfrac{1}{3}L^2\dot{\theta}^2 + L\dot{\theta}\dot{y}_O\cos\theta | ||
| + | \right). | ||
| + | </math> | ||
| + | </center> | ||
| + | La energía potencial gravitatoria es | ||
| + | <center> | ||
| + | <math> | ||
| + | U = -\dfrac{1}{2}mgL\cos\theta. | ||
| + | </math> | ||
| + | </center> | ||
| + | La función de Lagrange es | ||
| + | <center> | ||
| + | <math> | ||
| + | L = T - U = | ||
| + | \dfrac{1}{2}m\,\left( \dot{y}_O^2 + \dfrac{1}{3}L^2\dot{\theta}^2 + L\dot{\theta}\dot{y}_O\cos\theta | ||
| + | \right) + \dfrac{1}{2}mgL\cos\theta. | ||
| + | </math> | ||
| + | </center> | ||
| + | Ahora tenemos dos ecuaciones de Lagrange impulsivas | ||
| + | <center> | ||
| + | <math> | ||
| + | \Delta p_{\theta} = \hat{Q}^{NC}_{\theta}, | ||
| + | \qquad\qquad | ||
| + | \Delta p_{y_O} = \hat{Q}^{NC}_{y_O} | ||
| + | </math> | ||
| + | </center> | ||
| + | Tenemos | ||
| + | <center> | ||
| + | <math> | ||
| + | \begin{array}{l} | ||
| + | p_{\theta} = \dfrac{\partial L}{\partial \dot{\theta}} = \dfrac{1}{3}mL^2\dot{\theta} + \dfrac{1}{2}mL\dot{y}_O\cos\theta, | ||
| + | \\ | ||
| + | \\ | ||
| + | p_{y_O} = \dfrac{\partial L}{\partial \dot{y}_O} = m\dot{y}_O + \dfrac{1}{2}mL\dot{\theta}\cos\theta. | ||
| + | \end{array} | ||
| + | </math> | ||
| + | </center> | ||
| + | Las variaciones de momentos generalizados durante la percusión son | ||
| + | <center> | ||
| + | <math> | ||
| + | \begin{array}{l} | ||
| + | \Delta p_{\theta} = \dfrac{1}{3}mL^2\dot{\theta}^+ + \dfrac{1}{2}mL\dot{y}^+_O | ||
| + | \\ \\ | ||
| + | \Delta p_{y_O} = m\dot{y}_O^+ + \dfrac{1}{2}mL\dot{\theta}^+. | ||
| + | \end{array} | ||
| + | </math> | ||
| + | </center> | ||
| + | Hemos usado que durante la percusión <math>\theta=0</math> y que la barra parte del reposo. | ||
| + | |||
| + | La percusiones generalizadas son | ||
| + | <center> | ||
| + | <math> | ||
| + | \begin{array}{l} | ||
| + | \hat{Q}^{NC}_{\theta} = | ||
| + | \vec{\hat{F}}\cdot\dfrac{\partial\vec{v}^{\,P}_{21}}{\partial\dot{\theta}} | ||
| + | + | ||
| + | \vec{\hat{O}}_y\cdot\dfrac{\partial\vec{v}^{\,O}_{21}}{\partial\dot{\theta}} | ||
| + | = x_P\hat{F}_0 | ||
| + | \\ \\ | ||
| + | \hat{Q}^{NC}_{y_O} = | ||
| + | \vec{\hat{F}}\cdot\dfrac{\partial\vec{v}^{\,P}_{21}}{\partial\dot{y_O}} | ||
| + | + | ||
| + | \vec{\hat{O}}_y\cdot\dfrac{\partial\vec{v}^{\,O}_{21}}{\partial\dot{y_O}} | ||
| + | = \hat{F}_0 + \hat{O}_y. | ||
| + | \end{array} | ||
| + | </math> | ||
| + | </center> | ||
| + | Hay que recordar que <math>\vec{v}^{\,P}_{21}</math> se ve ahora modificada al liberar el vínculo. | ||
| + | |||
| + | Las ecuaciones impulsivas quedan | ||
| + | <center> | ||
| + | <math> | ||
| + | \begin{array}{l} | ||
| + | \dfrac{1}{3}mL^2\dot{\theta}^+ + \dfrac{1}{2}mL\dot{y}^+_O = x_P\hat{F}_O | ||
| + | \\ \\ | ||
| + | m\dot{y}_O^+ + \dfrac{1}{2}mL\dot{\theta}^+ = \hat{F}_O + \hat{O}_y. | ||
| + | \end{array} | ||
| + | </math> | ||
| + | </center> | ||
| + | Ahora volvemos a aplicar el vínculo que hemos liberado, es decir, <math>\dot{y}_O=0</math>. Con esto obetenemos | ||
| + | <center> | ||
| + | <math> | ||
| + | \begin{array}{l} | ||
| + | \dot{\theta}^+ = \dfrac{3x_P\hat{F}_0}{mL^2}, | ||
| + | \\ | ||
| + | \\ | ||
| + | \hat{O}_y = -\hat{F}_0\,\left(1-\dfrac{3x_P}{2L}\right). | ||
| + | \end{array} | ||
| + | </math> | ||
| + | </center> | ||
| + | Reobtenemos el resultado conseguido al aplicar la Dinámica vectorial. | ||
| + | |||
| + | [[Categoría:Problemas de Dinámica Impulsiva]] | ||
Revisión de 14:04 23 dic 2016
Contenido[ocultar] |
1 Enunciado
Una barra homogénea de longitud L está articulada en un punto fijo O de modo que puede colgar libremente, sometida a la acción de la gravedad. En el instante inicial se encuentra en reposo y colgando verticalmente. Se aplica un percusión horizontal hacia la derecha a una distancia xP del punto O. Determina la velocidad angular de la barra justo después de la percusión y las percusiones vinculares. Hazlo usando las herramientas de la Dinámica Vectorial y la Analítica.
2 Solución
2.1 Cinemática
Resolvemos primero la cinemática del problema para poder describir el movimiento. Tenemos
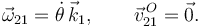
Tenemos un grado de libertad, la coordenada θ.
2.2 Dinámica vectorial
El vínculo en el punto O es que ese punto no se mueve. Al ser el problema plano, implica que hay dos componentes de percusión vincular que pueden ser no nulas. Las percusiones que actúan sobre la barra son
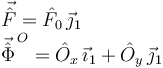
Tenemos tres incógnitas: 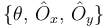 .
Tenemos que aplicar el T.C.M. impulsivo y el T.M.C. impulsivo.
.
Tenemos que aplicar el T.C.M. impulsivo y el T.M.C. impulsivo.
2.2.1 T.C.M.
Tenemos
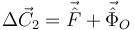
La gravedad no aparece en el proceso percusivo, pues es una fuerza de módulo acotado.
La cantidad de movimiento del centro de masas es
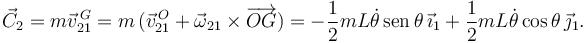
Durante la impulsión las coordenadas no cambian su valor. Además partimos del reposo. Por tanto tenemos
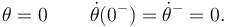
Entonces, la variación de la cantidad de movimiento es
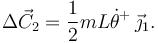
El T.C.M. impulsivo nos da dos ecuaciones escalares
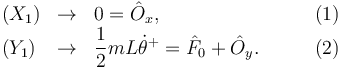
2.2.2 T.M.C.
Calculamos el momento cinético respecto del punto fijo O. La percusión vincular no ejerce momento respecto a este punto, por el T.C.M. impulsivo queda
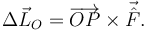
El momento cinético es
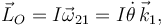
siendo el momento de inercia I = mL2 / 3. El cambio en el momento de inercia durante la percusión es
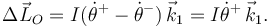
El momento percusivo es
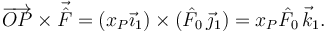
La ecuación que obtenemos de aplicar el T.M.C. impulsivo es
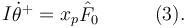
Resolviendo las tres ecuaciones obtenemos
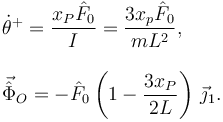
Vemos que si xP = 2L / 3, la percusión vincular se anula. Si esto ocurre, la velocidad del punto O es nula durante la percusión, y no hace falta que el vínculo actúa. Se dice entonces que el punto O es el centro de percusión del punto P.
2.2.3 Evolución posterior
Después de la percusión el movimiento de la barra se describe con los teoremas habituales (T.C.M., T.M.C. y energía). El resultado de la percusión se usa como condiciones iniciales de las ecuaciones obtenidas al aplicar los teoremas. En este caso las condiciones iniciales serían
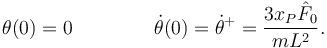
2.3 Dinámica analítica
El problema tiene un grado de libertad. Elegimos la coordenada generalizada {θ} para describirlo. La energía cinética es, usando que el punto O es un punto fijo
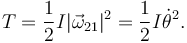
Para la energía potencial gravitatoria elegimos como origen de potencial la altura del eje Y1. Entonces
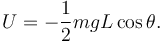
La Lagrangiana es
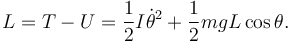
La ecuación de Lagrange impulsiva es
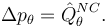
El momento generalizado es
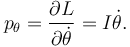
El cambio durante la percusión es

La percusión generalizada es
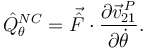
La velocidad es
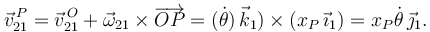
La percusión generalizada es
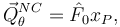
y la ecuación de Lagrange impulsiva queda
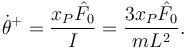
No obtenemos las percusiones vinculares pues no aparecen en la formulación analítica.
2.3.1 Calculo de percusiones vinculares con Dinámica analítica
Pueden calcularse las percusiones vinculares con las herramientas de la Dinámica analítica usando el Principio de Liberación o los Multiplicadores de Lagrange. Vamos a calcular la reacción percusiva horizontal en el punto O. Liberamos la restricción y = 0 para el punto O. Tenemos entonces dos grados de libertad y dos coordenadas generalizadas:  . Al liberar el vínculo, debemos introducir una percusión
. Al liberar el vínculo, debemos introducir una percusión
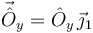
aplicada en el punto O.
Ahora la reducción cinemática en el punto O es

La velocidad del centro de masas de la barra es
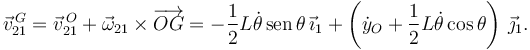
La energía cinética de la barra es
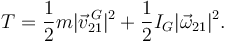
El momento de inercia es IG = mL2 / 12, pues es respecto al centro de masas. Tenemos
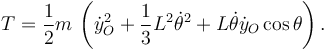
La energía potencial gravitatoria es
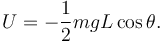
La función de Lagrange es
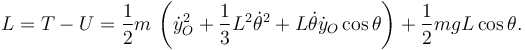
Ahora tenemos dos ecuaciones de Lagrange impulsivas

Tenemos
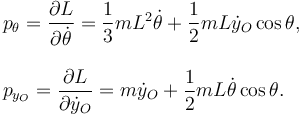
Las variaciones de momentos generalizados durante la percusión son
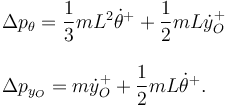
Hemos usado que durante la percusión θ = 0 y que la barra parte del reposo.
La percusiones generalizadas son
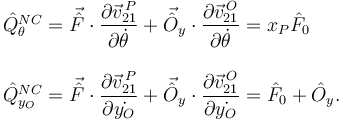
Hay que recordar que 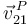 se ve ahora modificada al liberar el vínculo.
se ve ahora modificada al liberar el vínculo.
Las ecuaciones impulsivas quedan
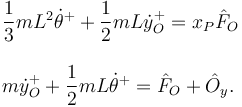
Ahora volvemos a aplicar el vínculo que hemos liberado, es decir,  . Con esto obetenemos
. Con esto obetenemos
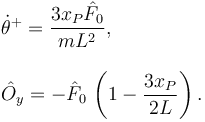
Reobtenemos el resultado conseguido al aplicar la Dinámica vectorial.