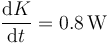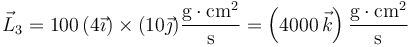Propiedades de un sistema de tres partículas

De Laplace

(Diferencias entre revisiones)

Revisión de 18:52 9 dic 2016

Contenido

1 Enunciado
2 Posición del centro de masas
3 Cantidad de movimiento
4 Momento cinético
- 4.1 Respecto al origen
- 4.2 Respecto al CM
5 Energía cinética
- 5.1 Respecto a un sistema fijo
- 5.2 Respecto al CM
6 Aceleraciones
7 Derivada del momento cinético
8 Derivada de la energía cinética

1 Enunciado

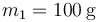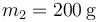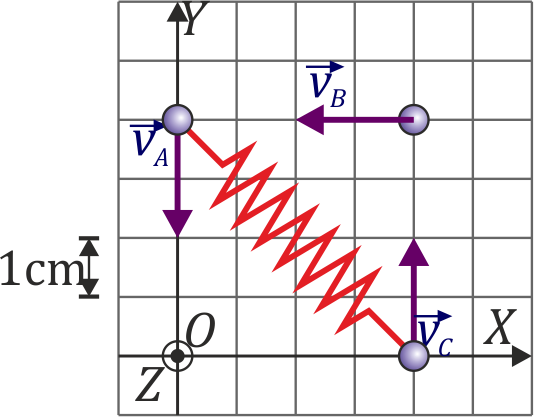
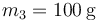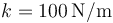Considere un sistema de tres partículas de masas $m_1=100\,\mathrm{g}$ , $m_2=200\,\mathrm{g}$ , $m_3=100\,\mathrm{g}$ que en un instante dado están situadas en las posiciones de la figura y moviéndose con la velocidad indicada, siendo la rapidez de cada una de ellas $10\,\mathrm{cm}/\mathrm{s}$ . Suponga que la masa 1 y la 3 está unidas por un resorte de longitud natural nula y constante $k=100\,\mathrm{N}/\mathrm{m}$ . Para el instante indicado

Halle la posición del centro de masas (CM) del sistema.
Calcule la cantidad de movimiento del sistema.
Halle el momento cinético respecto al origen y respecto al CM.
Calcule la energía cinética del sistema respecto a un sistema fijo y respecto al CM.
Halle la aceleración de cada masa y la del CM.
Halle la derivada respecto al tiempo del momento cinético (calculado respecto al origen).
Calcule la derivada respecto al tiempo de la energía cinética del sistema (calculada respecto a un sistema fijo).

2 Posición del centro de masas

La posición del centro de masas (CM) es la media ponderada de las tres posiciones

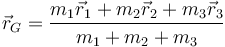
$\vec{r}_G = \frac{m_1\vec{r}_1+m_2\vec{r}_2+m_3\vec{r}_3}{m_1+m_2+m_3}$

Sustituyendo los diferentes valores

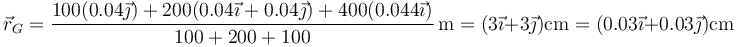
$\vec{r}_G = \frac{100(0.04\vec{\jmath})+200(0.04\vec{\imath}+0.04\vec{\jmath})+400(0.044\vec{\imath})}{100+200+100}\,\mathrm{m}=(3\vec{\imath}+3\vec{\jmath})\mathrm{cm}=(0.03\vec{\imath}+0.03\vec{\jmath})\mathrm{cm}$

3 Cantidad de movimiento

La cantidad de movimiento de un sistema es la suma de la de cada una de las partículas que lo componen

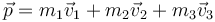
$\vec{p}=m_1\vec{v}_1+m_2\vec{v}_2+m_3\vec{v}_3$

y su valor en este caso es

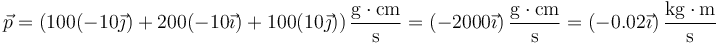
$\vec{p}=\left(100(-10\vec{\jmath})+200(-10\vec{\imath})+100(10\vec{\jmath})\right)\frac{\mathrm{g}\cdot\mathrm{cm}}{\mathrm{s}}=\left(-2000\vec{\imath}\right)\frac{\mathrm{g}\cdot\mathrm{cm}}{\mathrm{s}}=\left(-0.02\vec{\imath}\right)\frac{\mathrm{kg}\cdot\mathrm{m}}{\mathrm{s}}$

A partir de la cantidad de movimiento podemos hallar la velocidad del CM dividiendo por la masa total

$\vec{v}_G = \frac{\vec{p}}{M}=\left(\frac{-2000\vec{\imath}}{400}\right)\frac{\mathrm{cm}}{\mathrm{s}}= \left(-5\vec{\imath}\right)\frac{\mathrm{cm}}{\mathrm{s}}$

4 Momento cinético

4.1 Respecto al origen

El momento cinético es igual a la suma de los momentos cinéticos de las diferentes partículas respecto al mismo punto

$\vec{L}_O = m_1\vec{r}_1\times\vec{v}_1+m_2\vec{r}_2\times\vec{v}_2+m_3\vec{r}_3\times\vec{v}_3$

siendo cada uno

$\vec{L}_1 = 100\,(4\vec{\jmath})\times(-10\vec{\jmath})\frac{\mathrm{g}\cdot\mathrm{cm}^2}{\mathrm{s}}=\vec{0}$
$\vec{L}_2 = 200\,(4\vec{\imath}+4\vec{\jmath})\times(-10\vec{\imath})\frac{\mathrm{g}\cdot\mathrm{cm}^2}{\mathrm{s}}=\left(8000\,\vec{k}\right)\frac{\mathrm{g}\cdot\mathrm{cm}^2}{\mathrm{s}}$
$\vec{L}_3 = 100\,(4\vec{\imath})\times(10\vec{\jmath})\frac{\mathrm{g}\cdot\mathrm{cm}^2}{\mathrm{s}}=\left(4000\,\vec{k}\right)\frac{\mathrm{g}\cdot\mathrm{cm}^2}{\mathrm{s}}$

lo que nos da el total

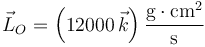
$\vec{L}_O=\left(12000\,\vec{k}\right)\frac{\mathrm{g}\cdot\mathrm{cm}^2}{\mathrm{s}}$

Cada uno de los momentos individuales se puede hallar observando que en módulo cumplen

$|\vec{L}_i|=m_id_i |\vec{v}_i|$

siendo $d i$ la distancia de O a la recta soporte de la velocidad (aquella que pasa por el punto y tiene la dirección de la velocidad). La dirección y el sentido de cada uno lo da la regla de la mano derecha.

4.2 Respecto al CM

El momento cinético se puede descomponer en una parte debida al movimiento con el CM más una parte debida al movimiento alrededor de éste

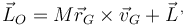
$\vec{L}_O=M\vec{r}_G\times\vec{v}_G+\vec{L}^{\,,}$

Podemos hallar el momento respecto al CM o bien empleando las posiciones y velocidades relativas

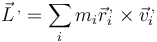
$\vec{L}^{\,,}=\sum_im_i\vec{r}_i^{\,,}\times\vec{v}^{\,,}_i$

o bien despejando de la expresión anterior

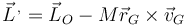
$\vec{L}^{\,,}=\vec{L}_O-M\vec{r}_G\times\vec{v}_G$

El momento cinético del sistema por moverse con el CM vale

$M\vec{r}_G\times\vec{v}_G = \vec{r}_G\times\vec{p}=\left(3\vec{\imath}+3\vec{\jmath}\right)\times(-2000\vec{\imath})\frac{\mathrm{g}\cdot\mathrm{cm}^2}{\mathrm{s}}=(6000\vec{k})\frac{\mathrm{g}\cdot\mathrm{cm}^2}{\mathrm{s}}$

por lo cual el momento cinético respecto al CM es la mitad del completo

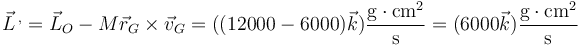
$\vec{L}^{\,,}=\vec{L}_O-M\vec{r}_G\times\vec{v}_G=((12000-6000)\vec{k})\frac{\mathrm{g}\cdot\mathrm{cm}^2}{\mathrm{s}}=(6000\vec{k})\frac{\mathrm{g}\cdot\mathrm{cm}^2}{\mathrm{s}}$

5 Energía cinética

5.1 Respecto a un sistema fijo

La energía cinética también es la suma de las individuales

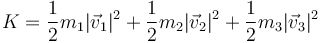
$K = \frac{1}{2}m_1|\vec{v}_1|^2+\frac{1}{2}m_2|\vec{v}_2|^2+\frac{1}{2}m_3|\vec{v}_3|^2$

En este ejemplo, en que las tres partículas se mueven con la misma rapidez, el cálculo es inmediato

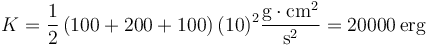
$K = \frac{1}{2}\left(100+200+100\right)(10)^2\frac{\mathrm{g}\cdot\mathrm{cm}^2}{\mathrm{s}^2} = 20000\,\mathrm{erg}$

siendo un ergio la unidad cegesimal de energía

$1\,\mathrm{erg} = 1\,\frac{\mathrm{g}\cdot\mathrm{cm}^2}{\mathrm{s}^2}=10^{-7}\mathrm{J}$

Empleando el SI para la energía cinética queda

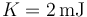
$K = 2\,\mathrm{mJ}$

5.2 Respecto al CM

Para la energía cinética se aplica una descomposición similar a la del momento cinético

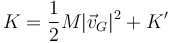
$K = \frac{1}{2}M|\vec{v}_G|^2+K'$

La energía cinética que tiene el sistema por moverse con el centro de masas es

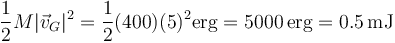
$\frac{1}{2}M|\vec{v}_G|^2 = \frac{1}{2}(400)(5)^2\mathrm{erg}= 5000\,\mathrm{erg}=0.5\,\mathrm{mJ}$

que es la cuarta parte de la total. La energía cinética del movimiento alrededor del CM lo forman los ¾ restantes

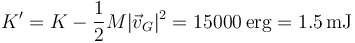
$K' = K-\frac{1}{2}M|\vec{v}_G|^2=15000\,\mathrm{erg}=1.5\,\mathrm{mJ}$

6 Aceleraciones

La aceleración de cada partícula es, de acuerdo con la segunda ley de Newton

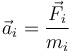
$\vec{a}_i=\frac{\vec{F}_i}{m_i}$

En este sistema no está sometida a fuerza alguna por lo que

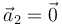
$\vec{a}_2 = \vec{0}$

mientras que la partícula 1 y la 3 está sometidas a una fuerza elástica, que cumple la ley de Hooke

$\vec{a}_1 = \frac{\vec{F}_{3\to 1}}{m_1}=\frac{-k(\vec{r}_1-\vec{r}_3)}{m_1}\qquad\qquad \vec{a}_3 = \frac{\vec{F}_{1\to 3}}{m_3}=\frac{-k(\vec{r}_3-\vec{r}_1)}{m_3}$

siendo la constante del muelle

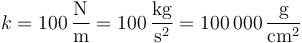
$k = 100\,\frac{\mathrm{N}}{\mathrm{m}} = 100\,\frac{\mathrm{kg}}{\mathrm{s}^2}=100\,000\,\frac{\mathrm{g}}{\mathrm{cm}^2}$

Esto nos da, para la aceleración de la partícula 1

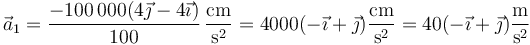
$\vec{a}_1=\frac{-100\,000(4\vec{\jmath}-4\vec{\imath})}{100}\,\frac{\mathrm{cm}}{\mathrm{s}^2} =4000(-\vec{\imath}+\vec{\jmath})\frac{\mathrm{cm}}{\mathrm{s}^2}=40(-\vec{\imath}+\vec{\jmath})\frac{\mathrm{m}}{\mathrm{s}^2}$

y para la partícula 3

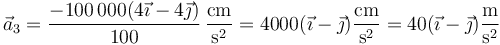
$\vec{a}_3=\frac{-100\,000(4\vec{\imath}-4\vec{\jmath})}{100}\,\frac{\mathrm{cm}}{\mathrm{s}^2} =4000(\vec{\imath}-\vec{\jmath})\frac{\mathrm{cm}}{\mathrm{s}^2}=40(\vec{\imath}-\vec{\jmath})\frac{\mathrm{m}}{\mathrm{s}^2}$

7 Derivada del momento cinético

La derivada del momento cinético respecto a un punto fijo O es la resultante del momento de las fuerzas externas aplicadas

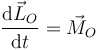
$\frac{\mathrm{d}\vec{L}_O}{\mathrm{d}t}=\vec{M}_O$

En este sistema, sin embargo, las únicas fuerzas que hay son internas, por lo que el momento cinético tiene derivada nula

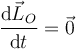
$\frac{\mathrm{d}\vec{L}_O}{\mathrm{d}t}=\vec{0}$

y es constante.

8 Derivada de la energía cinética

Para la energía cinética, a diferencia del momento cinético, si debemos tener en cuenta las fuerzas internas, siendo

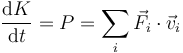
$\frac{\mathrm{d}K}{\mathrm{d}t}=P=\sum_i\vec{F}_i\cdot\vec{v}_i$

En nuestro caso, las únicas fuerzas que existen son las fuerzas elásticas sobre las partículas 1 y 3, siendo sus respectivas potencias

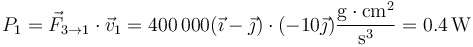
$P_1 = \vec{F}_{3\to 1}\cdot\vec{v}_1 = 400\,000(\vec{\imath}-\vec{\jmath})\cdot(-10\vec{\jmath})\frac{\mathrm{g}\cdot\mathrm{cm}^2}{\mathrm{s}^3}=0.4\,\mathrm{W}$

y

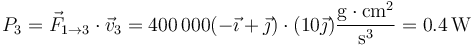
$P_3 = \vec{F}_{1\to 3}\cdot\vec{v}_3 = 400\,000(-\vec{\imath}+\vec{\jmath})\cdot(10\vec{\jmath})\frac{\mathrm{g}\cdot\mathrm{cm}^2}{\mathrm{s}^3}=0.4\,\mathrm{W}$

Para la partícula 2 la potencia es nula. Esto nos da para la derivada de la energía cinética en ese instante

$\frac{\mathrm{d}K}{\mathrm{d}t}=0.8\,\mathrm{W}$

@@ Línea 16: / Línea 16: @@
 La posición del centro de masas (CM) es la media ponderada de las tres posiciones
-<center><math>\vec{r}_C = \frac{m_1\vec{r}_1+m_2\vec{r}_2+m_3\vec{r}_3}{m_1+m_2+m_3}</math></center>
+<center><math>\vec{r}_G = \frac{m_1\vec{r}_1+m_2\vec{r}_2+m_3\vec{r}_3}{m_1+m_2+m_3}</math></center>
 Sustituyendo los diferentes valores
-<center><math>\vec{r}_C = \frac{100(4\vec{\jmath})+200(4\vec{\imath}+4\vec{\jmath})+400(4\vec{\imath})}{100+200+100}\,\mathrm{cm}=(3\vec{\imath}+3\vec{\jmath})\mathrm{cm}</math></center>
+<center><math>\vec{r}_G = \frac{100(0.04\vec{\jmath})+200(0.04\vec{\imath}+0.04\vec{\jmath})+400(0.044\vec{\imath})}{100+200+100}\,\mathrm{m}=(3\vec{\imath}+3\vec{\jmath})\mathrm{cm}=(0.03\vec{\imath}+0.03\vec{\jmath})\mathrm{cm}</math></center>
 ==Cantidad de movimiento==
@@ Línea 33: / Línea 33: @@
 A partir de la cantidad de movimiento podemos hallar la velocidad del CM dividiendo por la masa total
-<center><math>\vec{v}_C = \frac{\vec{p}}{M}=\left(\frac{-2000\vec{\imath}}{400}\right)\frac{\mathrm{cm}}{\mathrm{s}}= \left(-5\vec{\imath}\right)\frac{\mathrm{cm}}{\mathrm{s}}</math></center>
+<center><math>\vec{v}_G = \frac{\vec{p}}{M}=\left(\frac{-2000\vec{\imath}}{400}\right)\frac{\mathrm{cm}}{\mathrm{s}}= \left(-5\vec{\imath}\right)\frac{\mathrm{cm}}{\mathrm{s}}</math></center>
 ==Momento cinético==
@@ Línea 60: / Línea 60: @@
 El momento cinético se puede descomponer en una parte debida al movimiento con el CM más una parte debida al movimiento alrededor de éste
-<center><math>\vec{L}_O=M\vec{r}_C\times\vec{v}_C+\vec{L}^{\,,}</math></center>
+<center><math>\vec{L}_O=M\vec{r}_G\times\vec{v}_G+\vec{L}^{\,,}</math></center>
 Podemos hallar el momento respecto al CM o bien empleando las posiciones y velocidades relativas
@@ Línea 68: / Línea 68: @@
 o bien despejando de la expresión anterior
-<center><math>\vec{L}^{\,,}=\vec{L}_O-M\vec{r}_C\times\vec{v}_C</math></center>
+<center><math>\vec{L}^{\,,}=\vec{L}_O-M\vec{r}_G\times\vec{v}_G</math></center>
 El momento cinético del sistema por moverse con el CM vale
 <center><math>
-M\vec{r}_C\times\vec{v}_C = \vec{r}_C\times\vec{p}=\left(3\vec{\imath}+3\vec{\jmath}\right)\times(-2000\vec{\imath})\frac{\mathrm{g}\cdot\mathrm{cm}^2}{\mathrm{s}}=(6000\vec{k})\frac{\mathrm{g}\cdot\mathrm{cm}^2}{\mathrm{s}}</math></center>
+M\vec{r}_G\times\vec{v}_G = \vec{r}_G\times\vec{p}=\left(3\vec{\imath}+3\vec{\jmath}\right)\times(-2000\vec{\imath})\frac{\mathrm{g}\cdot\mathrm{cm}^2}{\mathrm{s}}=(6000\vec{k})\frac{\mathrm{g}\cdot\mathrm{cm}^2}{\mathrm{s}}</math></center>
 por lo cual el momento cinético respecto al CM es la mitad del completo
-<center><math>\vec{L}^{\,,}=\vec{L}_O-M\vec{r}_C\times\vec{v}_C=((12000-6000)\vec{k})\frac{\mathrm{g}\cdot\mathrm{cm}^2}{\mathrm{s}}=(6000\vec{k})\frac{\mathrm{g}\cdot\mathrm{cm}^2}{\mathrm{s}}</math></center>
+<center><math>\vec{L}^{\,,}=\vec{L}_O-M\vec{r}_G\times\vec{v}_G=((12000-6000)\vec{k})\frac{\mathrm{g}\cdot\mathrm{cm}^2}{\mathrm{s}}=(6000\vec{k})\frac{\mathrm{g}\cdot\mathrm{cm}^2}{\mathrm{s}}</math></center>
 ==Energía cinética==
@@ Línea 99: / Línea 99: @@
 Para la energía cinética se aplica una descomposición similar a la del momento cinético
-<center><math>K = \frac{1}{2}M|\vec{v}_C|^2+K'</math></center>
+<center><math>K = \frac{1}{2}M|\vec{v}_G|^2+K'</math></center>
 La energía cinética que tiene el sistema por moverse con el centro de masas es
-<center><math>\frac{1}{2}M|\vec{v}_C|^2 = \frac{1}{2}(400)(5)^2\mathrm{erg}= 5000\,\mathrm{erg}=0.5\,\mathrm{mJ}</math></center>
+<center><math>\frac{1}{2}M|\vec{v}_G|^2 = \frac{1}{2}(400)(5)^2\mathrm{erg}= 5000\,\mathrm{erg}=0.5\,\mathrm{mJ}</math></center>
 que es la cuarta parte de la total. La energía cinética del movimiento alrededor del CM lo forman los ¾ restantes
-<center><math>K' = K-\frac{1}{2}M|\vec{v}_C|^2=15000\,\mathrm{erg}=1.5\,\mathrm{mJ}</math></center>
+<center><math>K' = K-\frac{1}{2}M|\vec{v}_G|^2=15000\,\mathrm{erg}=1.5\,\mathrm{mJ}</math></center>
 ==Aceleraciones==

Propiedades de un sistema de tres partículas

De Laplace

Revisión de 18:52 9 dic 2016

Contenido

1 Enunciado

2 Posición del centro de masas

3 Cantidad de movimiento

4 Momento cinético

4.1 Respecto al origen

4.2 Respecto al CM

5 Energía cinética

5.1 Respecto a un sistema fijo

5.2 Respecto al CM

6 Aceleraciones

7 Derivada del momento cinético

8 Derivada de la energía cinética

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES