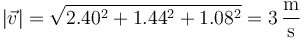Entrar Página Discusión Historial Go to the site toolbox

Caso de movimiento con aceleración constante (GIE)

De Laplace

(Diferencias entre revisiones)
Línea 53: Línea 53:
<center><math>
<center><math>
\begin{array}{rcccl}\vec{v}_0+\dfrac{1}{2}\vec{a}_0 &= & \vec{r}_1-\vec{r}_0 & = & 1.70\vec{\imath} -0.48\vec{\jmath}-0.36\vec{k}\\ &&&& \\
\begin{array}{rcccl}\vec{v}_0+\dfrac{1}{2}\vec{a}_0 &= & \vec{r}_1-\vec{r}_0 & = & 1.70\vec{\imath} -0.48\vec{\jmath}-0.36\vec{k}\\ &&&& \\
-
\vec{v}_0+\vec{a}_0& =& \dfrac{\vec{r}_2-\vec{r}_0}{2}& = & 2.40\vec{\imath}+1.44\vec{\jmath}+1.08\vec{k}</math></center>
+
\vec{v}_0+\vec{a}_0& =& \dfrac{\vec{r}_2-\vec{r}_0}{2}& = & 2.40\vec{\imath}+1.44\vec{\jmath}+1.08\vec{k}\end{array}</math></center>
(este úlltimo vector ya lo habíamos calculado en el primer apartado). Restamos la primera de la segunda y hallamos la aceleración
(este úlltimo vector ya lo habíamos calculado en el primer apartado). Restamos la primera de la segunda y hallamos la aceleración

Revisión de 21:16 12 nov 2016

Contenido

1 Enunciado

Una partícula se mueve con aceleración constante, de forma que en tres instantes sucesivos ocupa las siguientes posiciones

t(s) 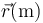\vec{r} (\mathrm{m})
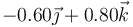
0\, -0.60\vec{\jmath}+0.80\vec{k}
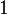
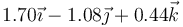
1\, 1.70\vec{\imath}-1.08\vec{\jmath}+0.44\vec{k}
2\, 4.80\vec{\imath}+2.28\vec{\jmath}+2.96\vec{k}
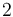
  1. Halle la velocidad media en el intervalo (0 s,2 s)
  2. Demuestre que la velocidad instantánea inicial (en t = 0\,\mathrm{s}) y la aceleración del movimiento valen

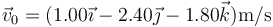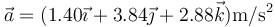
\vec{v}_0=(1.00\vec{\imath}-2.40\vec{\jmath}-1.80\vec{k})\mathrm{m}/\mathrm{s} y \vec{a}=(1.40\vec{\imath}+3.84\vec{\jmath}+2.88\vec{k})\mathrm{m}/\mathrm{s}^2

  1. Para el instante t = 1\,\mathrm{s}, halle:
    1. La velocidad, la rapidez y la aceleración instantáneas
    2. La aceleración tangencial y la aceleración normal (escalares)
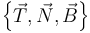
    3. Los vectores del triedro de Frenet \left\{\vec{T},\vec{N},\vec{B}\right\}
    4. El radio de curvatura y el centro de curvatura.

2 Velocidad media

En lo que sigue todas las cantidades con dimensiones están en las unidades fundamentales del SI: m, s o combinaciones de estos.

La velocidad media en un intervalo es el vector

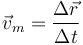
\vec{v}_m=\frac{\Delta\vec{r}}{\Delta t}

que en el intervalo (0 s,2 s) da

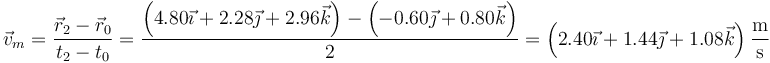
\vec{v}_m=\frac{\vec{r}_2-\vec{r}_0}{t_2-t_0}=\frac{\left(4.80\vec{\imath}+2.28\vec{\jmath}+2.96\vec{k}\right)-\left(-0.60\vec{\jmath}+0.80\vec{k}\right)}{2}=\left(2.40\vec{\imath}+1.44\vec{\jmath}+1.08\vec{k}\right)\frac{\mathrm{m}}{\mathrm{s}}

3 Velocidad inicial y aceleración

Al ser un movimiento de aceleración constante (aunque no rectilíneo; en general este tipo de movimientos es parabólico), la posición y la velocidad cumplen, en cada instante

\vec{r}(t)=\vec{r}_0+\vec{v}_0t+\frac{1}{2}\vec{a}_0t^2\qquad\qquad \vec{v}(t)=\vec{v}_0+\vec{a}_0t

Para determinar los coeficientes de una parábola basta imponer la posición de tres puntos. En este caso en concreto ya tenemos el coeficiente 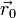\vec{r}_0. Aplicando la ecuación del movimiento con aceleración constante a los instantes t = 1 s y t = 2s queda

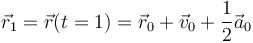
\vec{r}_1=\vec{r}(t=1)=\vec{r}_0+\vec{v}_0+\frac{1}{2}\vec{a}_0

y

\vec{r}_2=\vec{r}(t=2)=\vec{r}_0+2\vec{v}_0+2\vec{a}_0

Sustituimos los vectores de posición y obtenemos el sistema

\begin{array}{rcccl}\vec{v}_0+\dfrac{1}{2}\vec{a}_0 &= & \vec{r}_1-\vec{r}_0 & = & 1.70\vec{\imath} -0.48\vec{\jmath}-0.36\vec{k}\\ &&&& \\ \vec{v}_0+\vec{a}_0& =& \dfrac{\vec{r}_2-\vec{r}_0}{2}& = & 2.40\vec{\imath}+1.44\vec{\jmath}+1.08\vec{k}\end{array}

(este úlltimo vector ya lo habíamos calculado en el primer apartado). Restamos la primera de la segunda y hallamos la aceleración

\vec{a}_0=(1.40\vec{\imath}+3.84\vec{\jmath}+2.88\vec{k})\mathrm{m}/\mathrm{s}^2

y restando la segunda del doble de la primera hallamos la velocidad inicial

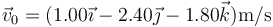
\vec{v}_0=(1.00\vec{\imath}-2.40\vec{\jmath}-1.80\vec{k})\mathrm{m}/\mathrm{s}

Alternativamente, como en el propio enunciado se da el resultado, es posible probarlo comprobando que en t = 1 s y en t = 2 s se obtiene el resultado dado en la tabla (hace falta sustituir en los dos instantes, no basta uno).

4 Magnitudes en t = 1s

4.1 Velocidad, rapidez y aceleración

Por tratarse de un movimiento con aceleración constante, la aceleración en t = 1 s es la misma que en t = 0 s

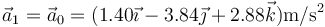
\vec{a}_1=\vec{a}_0=(1.40\vec{\imath}-3.84\vec{\jmath}+2.88\vec{k})\mathrm{m}/\mathrm{s}^2

mientras que la velocidad en este instante vale

\vec{v}_1=\vec{v}(t=1)=\vec{v}_0+\vec{a}_0=2.40\vec{\imath}+1.44\vec{\jmath}+1.08\vec{k}

Esta velocidad instantánea coincide con la velocidad media calculada en el primer apartado. Es una cosnecuencia del movimiento con aceleración constante: en un intervalo, la velocidad media coincide con la media aritmética de las velocidades en los extremos y con la velocidad instantánea en el centro del intervalo.

La rapidez es el módulo de esta velocidad

\left|\vec{v}\right|=\sqrt{2.40^2+1.44^2+1.08^2}=3\,\frac{\mathrm{m}}{\mathrm{s}}

4.2 Componentes intrínsecas de la aceleración

4.3 Triedro de Frenet

4.4 Radio y centro de curvatura

Obtenido de "http://tesla.us.es/wiki/index.php/Caso_de_movimiento_con_aceleraci%C3%B3n_constante_(GIE)"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Aviso legal - Acerca de Laplace