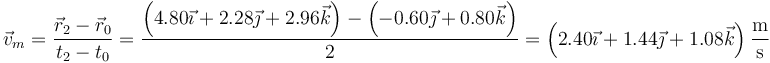Caso de movimiento con aceleración constante (GIE)
De Laplace
(Diferencias entre revisiones)
(→Enunciado) |
|||
| Línea 26: | Línea 26: | ||
==Velocidad media== | ==Velocidad media== | ||
| + | La velocidad media en un intervalo es el ''vector'' | ||
| + | |||
| + | <center><math>\vec{v}_m=\frac{\Delta\vec{r}}{\Delta t}</math></center> | ||
| + | |||
| + | que en el intervalo (0s,2s) da | ||
| + | |||
| + | <center><math>\vec{v}_m=\frac{\vec{r}_2-\vec{r}_0}{t_2-t_0}=\frac{\left(4.80\vec{\imath}+2.28\vec{\jmath}+2.96\vec{k}\right)-\left(-0.60\vec{\jmath}+0.80\vec{k}\right)}{2}=\left(2.40\vec{\imath}+1.44\vec{\jmath}+1.08\vec{k}\right)\frac{\mathrm{m}}{\mathrm{s}}</math></center> | ||
| + | |||
| + | |||
==Velocidad inicial y aceleración== | ==Velocidad inicial y aceleración== | ||
==Magnitudes en t = 1s== | ==Magnitudes en t = 1s== | ||
Revisión de 20:12 12 nov 2016
Contenido |
1 Enunciado
Una partícula se mueve con aceleración constante, de forma que en tres instantes sucesivos ocupa las siguientes posiciones
| t(s) |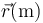 
|
|---|---|
| 
|
| 
|
| 
|
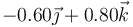
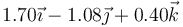
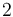
- Halle la velocidad media en el intervalo (0 s,2 s)
- Demuestre que la velocidad instantánea inicial (en
) y la aceleración del movimiento valen
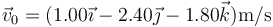y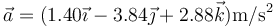 
- Para el instante
, halle:
- La velocidad, la rapidez y la aceleración instantáneas
- La aceleración tangencial y la aceleración normal (escalares)
- Los vectores del triedro de Frenet
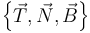
- El radio de curvatura y el centro de curvatura.
2 Velocidad media
La velocidad media en un intervalo es el vector
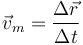
que en el intervalo (0s,2s) da
