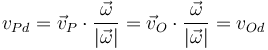Movimientos rígidos (CMR)
De Laplace
(→Teorema de Euler. Eje de rotación) |
(→Campo de velocidades) |
||
| Línea 186: | Línea 186: | ||
===Cambio del centro de reducción=== | ===Cambio del centro de reducción=== | ||
| + | En un movimiento general, sin punto fijo, el punto O no tiene nada de especial. Si consideramos como referencia otro punto A obtenemos | ||
| + | |||
| + | <center><math>\vec{v}_P=\vec{v}_O+\vec{\omega\times\left(\overrightarrow{OA}+\overrightarrow{AP}\right)=\vec{v}_A+\vec{\omega}\times\overrightarrow{AP}</math></center> | ||
| + | |||
| + | es, decir, para cualquier par de puntos se cumple | ||
| + | |||
| + | <center><math>\vec{v}_P=\vec{v}_A+\vec{\omega}\times\overrightarrow{AP}</math></center> | ||
| + | |||
| + | o dicho de otra forma, para conocer la velocidad instantánea de cualquier punto basta con conocer la velocidad angular (misma para todos) y la velocidad de un punto cualquiera. Al par <math>\{\vec{\omega},\vec{v}_A\}</math> se lo denomina ''reducción cinemática'' del campo de velocidades en el punto A. | ||
| + | |||
| + | ===Propiedades del campo de velocidades=== | ||
| + | ====Invariantes==== | ||
| + | Hay dos cantidades que son iguales para todos los puntos del sólido: | ||
| + | |||
| + | ;Velocidad angular: Es el ''invariante vectoral'' <math>\vec{\omega}</math> que, como hemos visto aparece en cualquier reducción cinemática. Es decir que cualquiera que sea el punto de referencia que tomemos, vemos al sólido girar instantáneamente con la misma velocidad angular. | ||
| + | |||
| + | ;Velocidad de deslizamiento: Es el ''invariante escalar''. Si calculamos la componente de la velocidad de cada punto en la dirección de la velocidad angular tenemos | ||
| + | |||
| + | <center><math>v_{Pd}=\vec{v}_P\cdot\frac{\vec{\omega}}{|\vec{\omega}|} = \vec{v}_O\cdot\frac{\vec{\omega}}{|\vec{\omega}|}=v_{Od}</math></center> | ||
==Campo de aceleraciones== | ==Campo de aceleraciones== | ||
Revisión de 14:19 9 nov 2016
Contenido |
1 El modelo del sólido rígido
1.1 Condición geométrica de rigidez
1.2 Condición cinemática de rigidez
2 Sólidos y sistemas de referencia
3 Movimientos rígidos finitos. Matriz de rotación
Un movimiento rígido de un sólido es aquel que preserva las distancias entre cada par de puntos, de forma que si una partícula se encuentra inicialmente en el punto A0 y posteriormente en el punto A y lo mismo co partículas B, C,… se cumple en todo instante
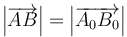
y al cumplirse para todos los puntos esto implica igualmente la conservación de los ángulos
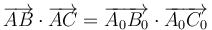
Existen diferentes transformaciones que mantienen las distancias y los ángulos:
- Traslaciones
- Todos los puntos experimentan el mismo desplazamiento, preservándose la orientación del sólido

- Rotaciones
- Existe al menos un punto cuya posición no se ve modificada. El resto e puntos experimenta un desplzamiento perpendicular a dicho eje.
- Simetría
- Se invierten las posiciones respecto a un plano de simetría. Un movimiento real de un sólido nunca puede consistir en una simetría (debería “volverse del revés”) por lo que no las consideremos en este artículo.
Un teorema crucial en la cinemática del sólido es que todo movimiento real puede descomponerse en una traslación y una rotación.
Para ello consideramos un partícula del sólido que inicialmente se hallaba en A0 y posteriormente en A. Este punto experimenta un desplazamiento
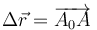
Supongamos que sometemos a todo el sólido a una traslación 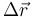 . para pasar de este estado intermedio al estado final debemos efectuar otro movimiento rígido en el que A es un punto fijo (porque ya se ha movido todo lo que se tenía que mover). Este segundo movimiento será entonces una rotacón alrededor de A.
. para pasar de este estado intermedio al estado final debemos efectuar otro movimiento rígido en el que A es un punto fijo (porque ya se ha movido todo lo que se tenía que mover). Este segundo movimiento será entonces una rotacón alrededor de A.
El punto A no tiene nada de especial. Podemos aplicar el mismo razonamiento a cualquier otro punto de referencia y el resultado es el mismo, es más, aunque el desplazamiento variará en cada caso, la rotación que debemos efectuar es independiente del punto de referencia que hayamos tomado.
Para ello consideramos el movimiento respecto a un punto dado A del sólido. Este punto experimenta un cierto desplazamiento. El resto de los puntos experimenta el mismo desplazamiento que A más un movimiento rígido alrededor de A, que constituye una rotación.
3.1 Expresión de las traslaciones
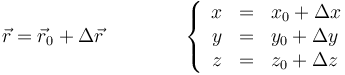
En términos de las componentes cartesianas, una traslación se calcula sumando las componentes del desplazamiento
3.2 Expresión de las rotaciones
Supongamos que en una rotación el punto fijo es O, que tomaremos como origen de coordenadas. En una rotación, cualquier punto pasará de la posición
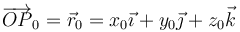
a la posición
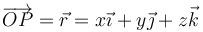
Deseamos establecer la relación entre estos dos vectores.
Para ello, emplearemos dos sistemas de referencia. El sistema “1” es el que consideramos fijo y respecto al cual se mueve el sólido. Los dos vectores que acabamos de escribir estarían expresados en la base 1. El otro (“0”) es uno móvil que gira con el sólido en todo momento.
En ese caso, al estar ligado al sólido, la posición de los puntos de éste son constantes en todo momento. Es decir, la posición de P
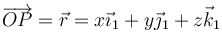
se expresará en la base 0
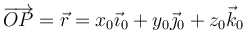
Nótese que en ambos casos se trata del mismo vector, expresado en dos bases distintas.
Para hallar las componentes en la base 1 proyectamos sobre cada vector de esta base
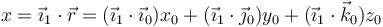
y análogamente para las otras dos componentes. Podemos escribir este resultado en forma matricial
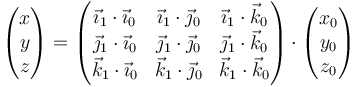
que podemos abreviar como
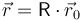
donde 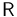 es la matriz de rotación que relaciona las componentes iniciales del vector de posición (o las que tiene en una base ligada al sólido) con las que tiene en un instante posterior. Esta matriz será función del tiempo.
es la matriz de rotación que relaciona las componentes iniciales del vector de posición (o las que tiene en una base ligada al sólido) con las que tiene en un instante posterior. Esta matriz será función del tiempo.
Vemos que los elementos de la matriz de rotación son los productos escalares entre los vectores de la base fija en el sólido y la fija en el laboratorio. Por ser unitarios todos los vectores estos elementos son los cosenos directores
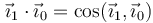
Asmismo, cada fila corresponde a las componentes de un vector de la base fija (1) expresado en la base ligada al sólido (0), y cada columna un vector de la base ligada al sólido expresado en la base fija. Simbólicamente
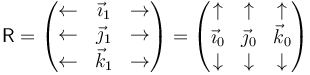
3.2.1 Propiedades de la matriz de rotación
- Tiene tres grados de libertad
- De acuerdo con la expresión anterior, parece que para expresar una rotación hay que proporcionar 9 parámetros, esto es, que tiene 9 grados de libertad. No es así, ya que tenemos seis vínculos entre las componentes. Por ser ortonormal cada base
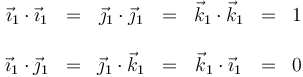
- Estos seis vínculos reducen el número de grados de libertad a 3, que pueden ser tres ángulos de orientación, como los ángulos de Euler.
- Es ortogonal
- Una matriz es ortogonal cuando su traspuesta coincide con su inversa. Si una rotación dada lleva de la base 1 a la base 0, la rotación inversa será la que devuelve la base 0 a la base 1. Por la construcción de la matriz, el intercambiar 1 por 0 equivale a intercambiar filas por columnas, esto es, hallar la traspuesta. Por tanto

- Esta propiedad equivale a lo que hemos mencionado de que las dos bases 0 y 1 son bases ortonormales.
- Es unitaria
- Una matriz es unitaria si su determinante vale la unidad. Es consecuencia inmediata de lo anterior
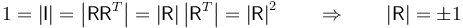
- La raíz negativa la descartamos, ya que corresponde a las simetrías, que hemos considerado como imposibles en el movimiento de un sólido real.
3.2.2 Teorema de Euler. Eje de rotación
Hemos definido como un movimiento rígido que deja un punto fijo. Euler demostró que esto implica que no hay un solo punto fijo, sino toda una recta que pasa por O. Esta recta es el llamado eje de rotación.
La demostración se basa en que debe haber un vector no afectado por la rotación, esto es,
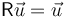
Si este vector  existe, cualquier múltiplo de él tampoco se verá afectado, con lo que obtenemos toda una recta que pasa por O.
existe, cualquier múltiplo de él tampoco se verá afectado, con lo que obtenemos toda una recta que pasa por O.
En términos algebraicos esto equivale a decir que existe un autovalor unidad, siendo 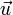 el autovector correspondiente. La condición para que ello ocurra es que
el autovector correspondiente. La condición para que ello ocurra es que
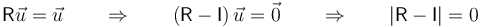
Veamos que es cierto:
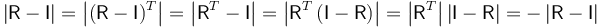
y por tanto

Por tanto existe el autovalor unidad, y el autovector correspondiente nos da el eje de rotación.
Esto nos da otra forma de parametricar las rotaciones: con dos ángulos (por ejemplo los de las coordenadas esféricas) damos la orientación de este vector director y con un tercer ángulo medimos cuánto ha girado el sólido en torno al eje.
Como consecuencia del teorema de Euler, cualquier vector perpendicular al eje de giro sigue siendo perpendicular tras la rotación. Si el vector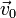
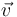
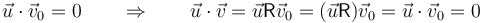
Cualquier otro vector podrá descomponerse en una parte paralela al eje de giro (que no se verá afectada por la rotación) más una parte ortogonal al eje (que gira un cierto ángulo en torno al eje, manteniéndose ortogonal).
3.3 Movimiento general. Teorema de Chasles
El caso general, según hemos visto, es una composición de una rotación y un desplazamiento en una dirección arbitraria.
Chasles generalizó el teorema de Euler, observando que ese desplzamiento arbitrario puede descomponerse en una traslación paralela al eje de rotación y en una ortogonal a él. la parte ortogonal puede englobarse en la rotación, quedando solo la paralela.
Por tanto, el movimiento general de un sólido se reduce a una rotación en torno a un eje y un desplazamiento en la dirección de este eje (que en este contexto se denomina eje de rotación y mínimo deslizamiento). Este movimiento se denomina “un tornillo” por su analogía con la conducta de esta herramienta.
4 Campo de velocidades
Cuando un sólido rígido se mueve efectúa en cada instante un movimiento rígido infinitesimal.
De acuerdo con el teorema de Chasles, este movimiento instantáneo se compondrá de una rotación diferencial alrededor de un eje (que ahora será eje instantáneo de rotación y mínimo deslizamiento, ya que puede cambiar de un instante a otro) y de un desplazamiento.
Si tomamos como referencia el punto O (“centro de reducción”) la velocidad de cualquier punto será la suma vectorial de la traslación de O más la rotación alrededor de un eje que pasa por O.
Para la velocidad de la rotación no tenemos más que considerar de nuevo qué le ocurre a la base ligada al sólido.
Si consideramos un punto P del sólido, su expresión en la bae ligada al sólido será
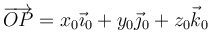
Este vector será constante en el sistema de referencia ligado al sólido, pero no en el sistema fijo 1. Si derivamos esta expresión solo son dependientes del tiempo los vectores de la base
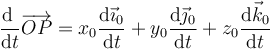
¿Cuánto vale la derivada respecto al tiempo de 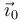 ? El extremo de este vector está realizando un movimiento circular instantáneo alrededor del eje de rotación y por tanto su velocidad cumple la relación
? El extremo de este vector está realizando un movimiento circular instantáneo alrededor del eje de rotación y por tanto su velocidad cumple la relación
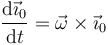
y lo mismo para los otros dos vectores de la base, que giran con la misma velocidad angular (esto no es trivial, pero puede demostrarse rigurosamente). Por tanto,
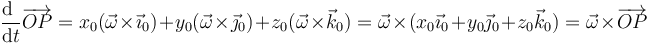
Por tanto, la velocidad debida a la rotación del sólido será, para todos los puntos,
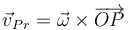
Aquí al vector 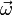 se lo denomina vector rotación del sólido o velocidad angular instantánea del sólido.
se lo denomina vector rotación del sólido o velocidad angular instantánea del sólido.
A esta velocidad habrá que sumarle la de la traslación del punto O, que será común para todos los puntos
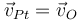
y por tanto la velocidad de cualquier punto del sólido es de la forma
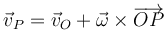
4.1 Cambio del centro de reducción
En un movimiento general, sin punto fijo, el punto O no tiene nada de especial. Si consideramos como referencia otro punto A obtenemos
es, decir, para cualquier par de puntos se cumple
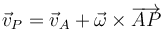
o dicho de otra forma, para conocer la velocidad instantánea de cualquier punto basta con conocer la velocidad angular (misma para todos) y la velocidad de un punto cualquiera. Al par 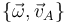 se lo denomina reducción cinemática del campo de velocidades en el punto A.
se lo denomina reducción cinemática del campo de velocidades en el punto A.
4.2 Propiedades del campo de velocidades
4.2.1 Invariantes
Hay dos cantidades que son iguales para todos los puntos del sólido:
- Velocidad angular
- Es el invariante vectoral
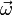 que, como hemos visto aparece en cualquier reducción cinemática. Es decir que cualquiera que sea el punto de referencia que tomemos, vemos al sólido girar instantáneamente con la misma velocidad angular.
que, como hemos visto aparece en cualquier reducción cinemática. Es decir que cualquiera que sea el punto de referencia que tomemos, vemos al sólido girar instantáneamente con la misma velocidad angular.
- Velocidad de deslizamiento
- Es el invariante escalar. Si calculamos la componente de la velocidad de cada punto en la dirección de la velocidad angular tenemos