Caso de movimiento con aceleración constante (GIE)
De Laplace
(Diferencias entre revisiones)
(→Enunciado) |
(→Enunciado) |
||
| Línea 18: | Línea 18: | ||
# Halle la velocidad media en el intervalo (0 s,2 s) | # Halle la velocidad media en el intervalo (0 s,2 s) | ||
# Demuestre que la velocidad instantánea inicial (en <math>t = 0\,\mathrm{s}</math>) y la aceleración del movimiento valen | # Demuestre que la velocidad instantánea inicial (en <math>t = 0\,\mathrm{s}</math>) y la aceleración del movimiento valen | ||
| - | <math>\vec{v}_0=(1.00\vec{\imath}-2.40\vec{\jmath}-1.80\vec{k})\mathrm{m}/\mathrm{s}</math> y <math>\vec{a}=(1.40\vec{\imath}-3.84\vec{\jmath}+2.88\vec{k})\mathrm{m}/\mathrm{s}^2</math> | + | <math>\vec{v}_0=(1.00\vec{\imath}-2.40\vec{\jmath}-1.80\vec{k})\mathrm{m}/\mathrm{s}</math> y <br /> <math>\vec{a}=(1.40\vec{\imath}-3.84\vec{\jmath}+2.88\vec{k})\mathrm{m}/\mathrm{s}^2</math> |
# Para el instante <math>t = 1\,\mathrm{s}</math>, halle: | # Para el instante <math>t = 1\,\mathrm{s}</math>, halle: | ||
## La velocidad, la rapidez y la aceleración instantáneas | ## La velocidad, la rapidez y la aceleración instantáneas | ||
Revisión de 23:54 7 nov 2016
Contenido |
1 Enunciado
Una partícula se mueve con aceleración constante, de forma que en tres instantes sucesivos ocupa las siguientes posiciones
| t(s) |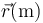 
|
|---|---|
| 
|
| 
|
| 
|
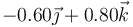
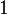
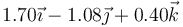
- Halle la velocidad media en el intervalo (0 s,2 s)
- Demuestre que la velocidad instantánea inicial (en
) y la aceleración del movimiento valen
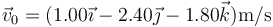y
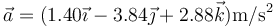
- Para el instante
, halle:
- La velocidad, la rapidez y la aceleración instantáneas
- La aceleración tangencial y la aceleración normal (escalares)
- Los vectores del triedro de Frenet
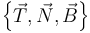
- El radio de curvatura y el centro de curvatura.
