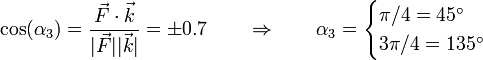Cálculo de las componentes de un vector
De Laplace
(→Solución) |
(→Solución) |
||
| (7 ediciones intermedias no se muestran.) | |||
| Línea 7: | Línea 7: | ||
La fuerza tendrá en general una componente en cada una de las tres direcciones del espacio | La fuerza tendrá en general una componente en cada una de las tres direcciones del espacio | ||
| - | <center><math>\vec{F}=F_x\vec{\imath}+F_y\vec{\jmath}+F_z\vec{k}</math></center> | + | <center><math>\vec{F}_1=F_x\vec{\imath}+F_y\vec{\jmath}+F_z\vec{k}</math></center> |
Para obtener cada una de ellas, multiplicamos por el vector unitario correspondiente. Así | Para obtener cada una de ellas, multiplicamos por el vector unitario correspondiente. Así | ||
| - | <center><math>F_x = \vec{F}\cdot\vec{\imath}</math></center> | + | <center><math>F_x = \vec{F}_1\cdot\vec{\imath}</math></center> |
Por otro lado, de la definición de producto escalar | Por otro lado, de la definición de producto escalar | ||
| - | <center><math>F_x = \vec{F}\cdot\vec{\imath}=|\vec{F}||\vec{\imath}|\cos(60^\circ) = (10\,\mathrm{N})\cdot 1\cdot \frac{1}{2}=5\,\mathrm{N}</math></center> | + | <center><math>F_x = \vec{F}_1\cdot\vec{\imath}=|\vec{F}_1||\vec{\imath}|\cos(60^\circ) = (10\,\mathrm{N})\cdot 1\cdot \frac{1}{2}=5\,\mathrm{N}</math></center> |
Análogamente | Análogamente | ||
| - | <center><math>F_y = \vec{F}\cdot\vec{\jmath}=|\vec{F}||\vec{\jmath}|\cos(60^\circ) = (10\,\mathrm{N})\cdot 1\cdot \frac{1}{2}=5\,\mathrm{N}</math></center> | + | <center><math>F_y = \vec{F}_1\cdot\vec{\jmath}=|\vec{F}_1||\vec{\jmath}|\cos(60^\circ) = (10\,\mathrm{N})\cdot 1\cdot \frac{1}{2}=5\,\mathrm{N}</math></center> |
| + | |||
| + | La tercera componente la hallamos a partir de estas dos y del módulo de la fuerza | ||
| + | |||
| + | <center><math>|\vec{F}_1|=\sqrt{F_x^2+F_y^2+F_z^2}\qquad\rightarrow\qquad F_z=\pm\sqrt{|\vec{F}_1|^2-F_x^2-F_y^2}</math></center> | ||
| + | |||
| + | Tenemos dos soluciones porque la tercera componente puede ir en la dirección del semieje OZ positivo o en la del negativo. Sustituyendo los valore snuméricos | ||
| + | |||
| + | <center><math>F_z =\pm\sqrt{100-25-25}\,\mathrm{N}=\pm 5\sqrt{2}\,\mathrm{N}=\pm 7.1\,\mathrm{N}</math></center> | ||
| + | |||
| + | Nótese que en el resultado final redondeamos a la cantidad de cifras significativas del dato de entrada (dos cifras). | ||
| + | |||
| + | Reuniendo los tres resultados, obtenemos las soluciones | ||
| + | |||
| + | <center><math>\vec{F}_1 = \left(5\vec{\imath}+5\vec{\jmath}\pm 7.1\vec{k}\right)\mathrm{N}</math></center> | ||
| + | |||
| + | Cuando a esta fuerza le sumamos la segunda | ||
| + | |||
| + | <center><math>\vec{F}_2 = \left(-10\,\vec{\imath}-10\,\vec{\jmath}\right)\,\mathrm{N}</math></center> | ||
| + | |||
| + | obtenemos la resultante | ||
| + | |||
| + | <center><math>\vec{F}=\vec{F}_1+\vec{F}_2 = \left(-5\vec{\imath}-5\vec{\jmath}\pm 7.1\vec{k}\right)\mathrm{N}</math></center> | ||
| + | |||
| + | El módulo de esta fuerza vale | ||
| + | |||
| + | <center><math>|\vec{F}|=\sqrt{(-5)^2+(-5)^2+(5\sqrt{2})^2}\,\mathrm{N}=10\,\mathrm{N}</math></center> | ||
| + | |||
| + | (a la hora de hacer cálculos intermedios interesa usar las soluciones exactas, y solo redondear en los resultados finales). | ||
| + | |||
| + | El ángulo que forma la fuerza con el eje OX positivo lo obtenemos a partir de sus coseno | ||
| + | |||
| + | <center><math>\cos(\alpha_1) = \frac{\vec{F}\cdot\vec{\imath}}{|\vec{F}||\vec{\imath}|} = -0.5\qquad \Rightarrow\qquad \alpha_1 = \frac{2\pi}{3}=120^\circ</math></center> | ||
| + | |||
| + | Análogamente para el eje OY | ||
| + | |||
| + | <center><math>\cos(\alpha_2) = \frac{\vec{F}\cdot\vec{\jmath}}{|\vec{F}||\vec{\jmath}|} = -0.5\qquad \Rightarrow\qquad \alpha_2 = \frac{2\pi}{3}=120^\circ</math></center> | ||
| + | |||
| + | Para el eje OZ operamos del mismo modo y tenemos dos posibilidades | ||
| + | |||
| + | <center><math>\cos(\alpha_3) = \frac{\vec{F}\cdot\vec{k}}{|\vec{F}||\vec{k}|} = \pm 0.7\qquad \Rightarrow\qquad \alpha_3 = \begin{cases}\pi/4 =45^\circ & \\ 3\pi/4 = 135^\circ & \end{cases}</math></center> | ||
[[Categoría:Problemas de herramientas matemáticas (GIE)]] | [[Categoría:Problemas de herramientas matemáticas (GIE)]] | ||
última version al 16:20 19 oct 2016
1 Enunciado
De una fuerza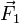 
se sabe que tiene de intensidad 10 N y que los ángulos que forma con los semiejes OX y OY positivos valen 60°. Determine las componentes cartesianas de esta fuerza. ¿Existe solución? ¿Es única?
Si a esta fuerza se le suma otra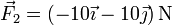 
, ¿qué ángulo forma la resultante con los ejes coordenados?
2 Solución
La fuerza tendrá en general una componente en cada una de las tres direcciones del espacio
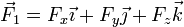
Para obtener cada una de ellas, multiplicamos por el vector unitario correspondiente. Así
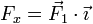
Por otro lado, de la definición de producto escalar
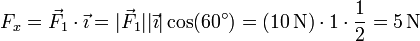
Análogamente
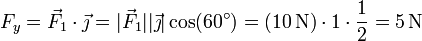
La tercera componente la hallamos a partir de estas dos y del módulo de la fuerza
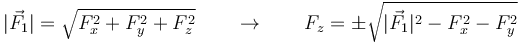
Tenemos dos soluciones porque la tercera componente puede ir en la dirección del semieje OZ positivo o en la del negativo. Sustituyendo los valore snuméricos
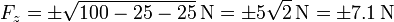
Nótese que en el resultado final redondeamos a la cantidad de cifras significativas del dato de entrada (dos cifras).
Reuniendo los tres resultados, obtenemos las soluciones
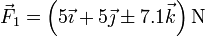
Cuando a esta fuerza le sumamos la segunda
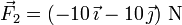
obtenemos la resultante
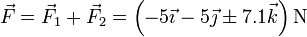
El módulo de esta fuerza vale
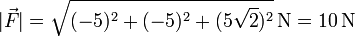
(a la hora de hacer cálculos intermedios interesa usar las soluciones exactas, y solo redondear en los resultados finales).
El ángulo que forma la fuerza con el eje OX positivo lo obtenemos a partir de sus coseno
Análogamente para el eje OY
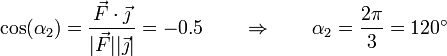
Para el eje OZ operamos del mismo modo y tenemos dos posibilidades
