Movimientos rígidos (CMR)
De Laplace
(→Movimientos rígidos finitos. Matriz de rotación) |
(→Expresión de las traslaciones) |
||
| Línea 31: | Línea 31: | ||
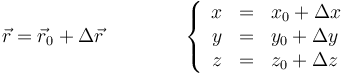
En términos de las componentes cartesianas, una traslación se calcula sumando las componentes del desplazamiento | En términos de las componentes cartesianas, una traslación se calcula sumando las componentes del desplazamiento | ||
| - | <center><math>\vec{r}=\vec{r}_0+\Delta \vec{r}\qquad\qquad \left\{ \begin{array}{rcl} x & = & x_0+ \Delta x \\ y & = & y_0+ \Delta y \\ z & = & z_0+ \Delta z \end{array}\ | + | <center><math>\vec{r}=\vec{r}_0+\Delta \vec{r}\qquad\qquad \left\{ \begin{array}{rcl} x & = & x_0+ \Delta x \\ y & = & y_0+ \Delta y \\ z & = & z_0+ \Delta z \end{array}\right.</math></center> |
===Expresión de las rotaciones=== | ===Expresión de las rotaciones=== | ||
Revisión de 19:05 18 oct 2016
Contenido |
1 El modelo del sólido rígido
1.1 Condición geométrica de rigidez
1.2 Condición cinemática de rigidez
2 Sólidos y sistemas de referencia
3 Movimientos rígidos finitos. Matriz de rotación
Un movimiento rígido de un sólido es aquel que preserva las distancias entre cada par de puntos, de forma que si una partícula se encuentra inicialmente en el punto A0 y posteriormente en el punto A y lo mismo co partículas B, C,… se cumple en todo instante
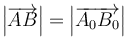
y al cumplirse para todos los puntos esto implica igualmente la conservación de los ángulos
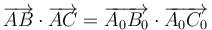
Existen diferentes transformaciones que mantienen las distancias y los ángulos:
- Traslaciones
- Todos los puntos experimentan el mismo desplazamiento, preservándose la orientación del sólido

- Rotaciones
- Existe al menos un punto cuya posición no se ve modificada. El resto e puntos experimenta un desplzamiento perpendicular a dicho eje.
- Simetría
- Se invierten las posiciones respectoa un plano de simetría. Un movimiento real de un sólido nunca puede consistir en una simetría (debería “volverse del revés”) por lo que no las consideremos en este artículo.
Un teorema crucial en la cinemática del sólido es que todo movimiento real puede descomponerse en una traslación y una rotación. Para ello consideramos el movimiento respecto a un punto dado A, de forma que
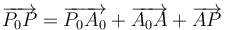
El término 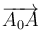 es el mismo para todos los puntos (no depende de P, solo de A), por lo que se puede interpretar como una traslación, y la suma
es el mismo para todos los puntos (no depende de P, solo de A), por lo que se puede interpretar como una traslación, y la suma 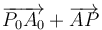 es en sí misma un movimiento rígido que tiene un punto fijo, el A, y por tanto se trata de una rotación.
es en sí misma un movimiento rígido que tiene un punto fijo, el A, y por tanto se trata de una rotación.
3.1 Expresión de las traslaciones
En términos de las componentes cartesianas, una traslación se calcula sumando las componentes del desplazamiento