Cantidad de movimiento (CMR)
De Laplace
| (12 ediciones intermedias no se muestran.) | |||
| Línea 1: | Línea 1: | ||
| - | + | ==Definición== | |
| - | + | ||
Se define la cantidad de movimiento de una partícula como el producto de su masa por su velocidad | Se define la cantidad de movimiento de una partícula como el producto de su masa por su velocidad | ||
| Línea 7: | Línea 6: | ||
Sus dimensiones son <math>MLT^{-1}</math> y sus unidades en el SI son <math>\mathrm{N}\cdot\mathrm{s}</math> (o <math>\mathrm{kg}\cdot\mathrm{m}/\mathrm{s}</math>) | Sus dimensiones son <math>MLT^{-1}</math> y sus unidades en el SI son <math>\mathrm{N}\cdot\mathrm{s}</math> (o <math>\mathrm{kg}\cdot\mathrm{m}/\mathrm{s}</math>) | ||
| - | + | ==Teorema de la cantidad de movimiento== | |
A partir de la definición es inmediato que | A partir de la definición es inmediato que | ||
| Línea 16: | Línea 15: | ||
En el caso de una sola partícula, el teorema de la cantidad de movimiento no es más que la segunda ley de Newton. Este teorema cobra interés cuando se generaliza a sistemas de partículas. | En el caso de una sola partícula, el teorema de la cantidad de movimiento no es más que la segunda ley de Newton. Este teorema cobra interés cuando se generaliza a sistemas de partículas. | ||
| - | + | ==Impulso== | |
En ocasiones, no nos interesa tanto saber cómo cambia la cantidad de movimiento en un intervalo de tiempo infinitesimal, sino saber cuánto varía durante un cierto periodo. Supongamos una partícula que viaja libremente y por tanto con cantidad de movimiento constante <math>\vec{p}_1</math>. Entonces es sometida a una fuerza <math>\vec{F}(t)</math> durante un intervalo entre <math>t_1</math> y <math>t_2</math> (por ejemplo, durante una colisión), a partir del cual vuelve a moverse libremente, con cantidad de movimiento constante <math>\vec{p}_2</math>. Se trata de hallar el incremento en la cantidad de movimiento durante la colisión. | En ocasiones, no nos interesa tanto saber cómo cambia la cantidad de movimiento en un intervalo de tiempo infinitesimal, sino saber cuánto varía durante un cierto periodo. Supongamos una partícula que viaja libremente y por tanto con cantidad de movimiento constante <math>\vec{p}_1</math>. Entonces es sometida a una fuerza <math>\vec{F}(t)</math> durante un intervalo entre <math>t_1</math> y <math>t_2</math> (por ejemplo, durante una colisión), a partir del cual vuelve a moverse libremente, con cantidad de movimiento constante <math>\vec{p}_2</math>. Se trata de hallar el incremento en la cantidad de movimiento durante la colisión. | ||
| Línea 35: | Línea 34: | ||
Esta relación, aparentemente trivial, tiene su importancia en la teoría de [[Colisiones_de_dos_part%C3%ADculas|colisiones]] y de percusiones, donde se ignora el valor exacto de la fuerza, pero sí se conoce el valor del impulso. | Esta relación, aparentemente trivial, tiene su importancia en la teoría de [[Colisiones_de_dos_part%C3%ADculas|colisiones]] y de percusiones, donde se ignora el valor exacto de la fuerza, pero sí se conoce el valor del impulso. | ||
| - | + | ==Teorema de conservación de la cantidad de movimiento== | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
De la segunda ley de Newton es inmediato que: | De la segunda ley de Newton es inmediato que: | ||
| Línea 104: | Línea 51: | ||
Para el caso de una partícula este teorema de conservación aporta poca información nueva. Sin embargo, su extensión al caso de un [[cantidad de movimiento de un sistema de partículas|sistema de partículas]] es extremadamente útil. | Para el caso de una partícula este teorema de conservación aporta poca información nueva. Sin embargo, su extensión al caso de un [[cantidad de movimiento de un sistema de partículas|sistema de partículas]] es extremadamente útil. | ||
| - | == | + | ==Conservación parcial de la cantidad de movimiento== |
| - | + | La cantidad de movimiento es un vector, con tres componentes cartesianas. Por ello, son posibles situaciones en las que, si bien no se conserva la cantidad de movimiento en su totalidad, sí sea constante alguna de sus componentes. Concretamente: | |
| - | + | :''Si la resultante de las fuerzas que actúan sobre una partícula es en todo instante perpendicular a la dirección marcada por un vector unitario <math>\vec{u}</math>, fijo, entonces se conserva la componente en dicha dirección'' | |
| - | + | <center><math>\vec{F}\cdot\vec{u}=0\qquad\forall t\qquad\Rightarrow\qquad p_u=\vec{p}\cdot\vec{u}=\mathrm{cte.}</math></center> | |
| - | + | Un ejemplo típico lo tenemos en el caso del movimiento por acción del peso (tiro parabólico). Al ser éste vertical en todo instante, las componentes horizontales de la cantidad de movimiento se conservan (no así la vertical). | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | La | + | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | :''Si la resultante | + | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | <center><math>\vec{F} | + | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ==Cantidad de movimiento de un sistema de partículas== | |
| + | La cantidad de movimiento (o momento lineal) del sistema es la suma de las cantidades de movimiento de cada una de las partículas | ||
| - | <center><math>\vec{ | + | <center><math>\vec{p} = \vec{p}_1+\vec{p}_2+\cdots = m_1\vec{v}_1+m_2\vec{v}_2 + \cdots </math></center> |
| - | + | ==Relación con el centro de masas== | |
| + | El [[Masa_y_Gentro_de_masas_(CMR)#Centro_de_masas_.28CM.29|centro de masas]] de un sistema de partículas se define como un punto cuya posición es la media ponderada de las posiciones respectivas. | ||
| - | <center><math>\ | + | <center><math>\overrightarrow{OG}=\frac{1}{M}\sum_i m_i \overrightarrow{OP}_i\qquad\qquad \vec{r}_G=\frac{1}{M}\sum_i \vec{r}_i</math></center> |
| - | + | ===Velocidad del centro de masas=== | |
| + | El centro de masas no es un punto fijo, sino que puede desplazarse cuando lo hacen las partículas del sistema. Obtenemos su velocidad derivando la definición respecto al tiempo | ||
| - | <center><math>\mathrm{d}\vec{ | + | <center><math> |
| + | \vec{v}_G = \frac{\mathrm{d}\vec{r}_G}{\mathrm{d}t} = \frac{1}{M}\sum_im_i\frac{\mathrm{d}\vec{r}_i}{\mathrm{d}t} = \frac{1}{M}\sum_im_i\vec{v}_i</math></center> | ||
| - | + | El numerador es justamente la cantidad de movimiento del sistema | |
| - | <center><math>\vec{ | + | <center><math>\vec{v}_G=\frac{\vec{p}}{M}\qquad\Rightarrow\qquad \vec{p}=M\vec{v}_G</math></center> |
| - | Por tanto | + | Por tanto, la cantidad de movimiento del sistema es la misma que tendría una sola partícula que concentrara la masa de todas y se moviera como el centro de masas. |
| - | + | ==Evolución de la cantidad de movimiento== | |
| + | Supongamos un sistema de partículas sometidas a fuerzas externas y también interactuantes entre sí, cumpliendo las fuerzas internas la tercera ley de Newton. En este caso, la variación en el tiempo de la cantidad de movimiento total es | ||
| - | + | <center><math>\frac{\mathrm{d}\vec{p}}{\mathrm{d}t} = m_1\frac{\mathrm{d}\vec{v}_1}{\mathrm{d}t}+ m_2\frac{\mathrm{d}\vec{v}_2}{\mathrm{d}t}+\cdots = \vec{F}_1+\vec{F}_2 + \cdots</math></center> | |
| - | + | esto es, la derivada de la cantidad de movimiento es la resultante de todas las fuerzas que actúan sobre las partículas del sistema. Esto es consecuencia directa de la definición, pero es poco útil pues requiere conocer también las fuerzas internas que son normalmente desconocidas. Por ello, descomponemos las fuerzas sobre cada partícula en suma de las externas y de las internas | |
| - | = | + | <center><math>\vec{F}_i = \vec{F}_{i\mathrm{ext}}+\vec{F}_{1\to i}+\vec{F}_{2\to i}+\cdots</math></center> |
| - | + | ||
| - | + | y la derivada de la cantidad de movimiento queda | |
| - | <center><math>\vec{ | + | <center><math>\frac{\mathrm{d}\vec{p}}{\mathrm{d}t}=\left(\vec{F}_{1\mathrm{ext}}+\vec{F}_{2\to 1}+\vec{F}_{3\to 1}+\cdots\right)+\left(\vec{F}_{2\mathrm{ext}}+\vec{F}_{1\to 2}+\vec{F}_{3\to 2}+\cdots\right)+\left(\vec{F}_{3\mathrm{ext}}+\vec{F}_{1\to 3}+\vec{F}_{2\to 3}+\cdots\right)+\cdots</math></center> |
| - | + | Pero, de acuerdo con la tercera ley de Newton | |
| - | <center><math>\vec{ | + | <center><math>\vec{F}_{1\to 2}+\vec{F}_{2\to 1} = \vec{0}</math></center> |
| - | + | y análogamente para el resto de pares de partículas. Por tanto, las fuerzas internas se cancelan dos a dos y queda la expresión mucho más útil | |
| - | <center><math> | + | <center><math>\frac{\mathrm{d}\vec{p}}{\mathrm{d}t}= \vec{F}_{1\mathrm{ext}}+\vec{F}_{2\mathrm{ext}}+\cdots = \vec{F}_{\mathrm{ext}}</math></center> |
| - | + | siendo <math>\vec{F}_\mathrm{ext}</math> la resultante de las fuerzas externas aplicadas, esto es | |
| - | + | * la derivada de la cantidad de movimiento es igual a la ''resultante'' de las fuerzas '''externas''' aplicadas sobre el sistema. | |
| - | En | + | En términos del centro de masas, la ley de evolución de la cantidad de movimiento se escribe |
| - | <center><math>\ | + | <center><math>\frac{\mathrm{d}\ }{\mathrm{d}t}\left(M\vec{v}_G\right) =\vec{F}_{\mathrm{ext}}</math></center> |
| - | + | es decir: | |
| - | + | * El centro de masas de un sistema de partículas se mueve como una sola partícula cuya masa fuera la total del sistema y que se encontrara sometida a la resultante de las fuerzas externas ejercidas sobre el sistema. | |
| - | + | En un sistema cerrado, en el que la masa total permanece constante, la derivada de la masa es cero y obtenemos | |
| - | <center><math>\ | + | <center><math>M\vec{a}_G = \vec{F}_\mathrm{ext}</math></center> |
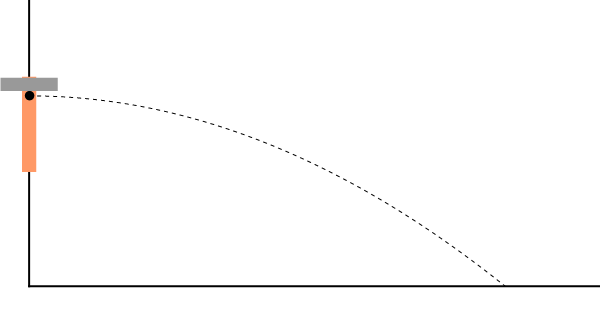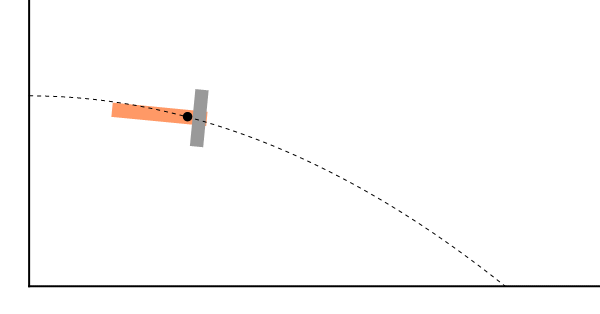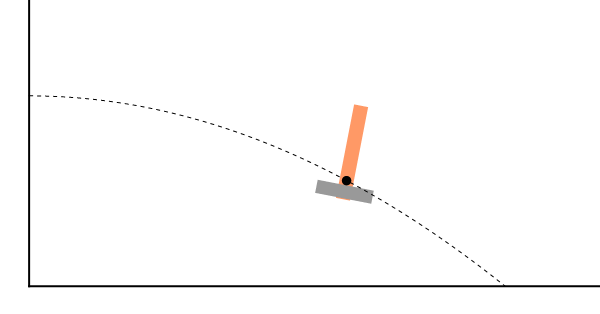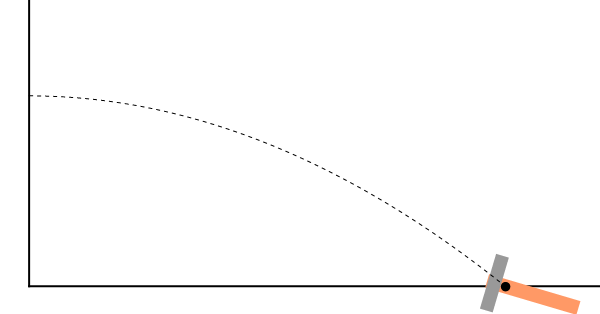
| - | + | Como ejemplo tenemos el lanzamiento de un objeto. Aunque las distintas partes del objeto pueden seguir trayectorias complicadas, su CM se mueve como una partícula sometida exclusivamente a la acción del peso, es decir, describe una parábola | |
| - | <center> | + | <center>[[Archivo:martillo-parabola.gif]]</center> |
| - | + | ==Conservación de la cantidad de movimiento== | |
| + | Del teorema de la cantidad de movimiento | ||
| - | = | + | <center><math>\frac{\mathrm{d}\vec{p}}{\mathrm{d}t}=\vec{F}_\mathrm{ext}</math></center> |
| - | + | ||
| - | + | se deduce de manera inmediata que: | |
| - | + | :''En un sistema de partículas tal que la resultante de las fuerzas externas es nula durante un cierto intervalo de tiempo, la cantidad de movimiento del sistema permanece constante durante dicho intervalo'' | |
| - | + | <center><math>\vec{F}_\mathrm{ext}=\vec{0}\qquad \forall t\qquad\Rightarrow\qquad \vec{p}=\vec{p}_0=\mathrm{cte}</math></center> | |
| - | + | En particular: | |
| - | + | :''En un sistema de partículas sometido exclusivamente a fuerzas internas la cantidad de movimiento del sistema permanece constante'' | |
| - | + | Asimismo, este teorema implica que | |
| - | + | ||
| - | + | :''El centro de masas de un sistema de partículas sometido exclusivamente a fuerzas internas describe un movimiento rectilíneo y uniforme'' | |
| - | + | Por tratarse de una identidad vectorial, es posible que se conserve alguna de las componentes de la cantidad de movimiento mientras que otras son variables. | |
| - | + | :''En un sistema de partículas tal que la resultante de las fuerzas externas es perpendicular a un vector fijo <math>\vec{u}</math> durante un cierto intervalo de tiempo, la componente de la cantidad de movimiento del sistema en la dirección de <math>\vec{u}</math> permanece constante durante dicho intervalo'' | |
| - | <center><math> | + | <center><math>\vec{F}_\mathrm{ext}\cdot\vec{u}=0\qquad \forall t\qquad\Rightarrow\qquad p_u=\vec{p}\cdot\vec{u}=\mathrm{cte}</math></center> |
| + | Este principio imposibilita que, por ejemplo, un grupo de aguerridos astronautas consiga desviar la trayectoria de un cometa simplemente colocando una bomba en él, ya que las fuerzas debidas a la bomba son puramente internas, y el centro de masas continuará su trayectoria inalterada, por mucho que se fragmente el asteroide. | ||
| - | + | ==Sistema de referencia del centro de masas== | |
| + | Una vez definida la posición del centro de masas, interesa indicar dónde están situadas las partículas respecto al CM. Esto se consigue definiendo la posición relativa | ||
| - | <center><math>\ | + | <center><math>{\vec{r}_i}^{\,\prime} = \vec{r}_i-\vec{r}_G\qquad\qquad \overrightarrow{GP}_i=\overrightarrow{OP}_i-\overrightarrow{OG}</math></center> |
| - | la | + | Dado que la posición del centro de masas respecto a sí mismo es evidentemente nula, se cumple |
| - | + | <center><math>\vec{0}=\vec{r}^{\,\prime}_G \qquad \Rightarrow\qquad \sum_im_i\vec{r}^{\,\prime}_i=m_1\vec{r}^{\,\prime}_1+m_2\vec{r}^{\,\prime}_2 +\cdots = \vec{0}\qquad\qquad \sum_im_i \overrightarrow{GP}_i=\vec{0}</math></center> | |
| - | + | De manera análoga se define la velocidad relativa al CM | |
| - | + | <center><math>{\vec{v}_i}^{\,\prime} = \vec{v}_i-\vec{v}_G</math></center> | |
| - | + | y, del mismo modo que con la posición | |
| - | + | <center><math>\vec{0}=\vec{v}^{\,\prime}_G \qquad \Rightarrow\qquad m_1\vec{v}^{\,\prime}_1 + m_2\vec{v}^{\,\prime}_2 +\cdots = \vec{0}</math></center> | |
| - | + | ya que el centro de masas no se mueve respecto a sí mismo. | |
| - | + | De la relación entre cantidad de movimiento y velocidad del centro de masas se llega a que la cantidad de movimiento del sistema respecto al centro de masas es siempre nula | |
| - | <center><math>\ | + | <center><math>\vec{p}^{\,\prime} = \sum_i m_i\vec{v}^{\,\prime}_i=M\vec{v}^{\,\prime}_G = \vec{0}</math></center> |
| - | + | Esto permite redefinir el centro de masas como aquel punto (variable) desde el cual la cantidad de movimiento del sistema es nula en todo momento. Cuando un sistema de partículas se estudia empleando este punto como origen del sistema de referencia se dice que se está estudiando desde el ''sistema centro de masas''. | |
| - | + | ==Sistema de referencia móvil== | |
| + | El caso del sistema CM es uno particular de sistema de referencia móvil. Si consideramos un caso más general de un sistema de referencia que se traslada (sin rotar) con una velocidad <math>\vec{v}_A</math>, la velocidad de las partículas respecto a este sistema es | ||
| - | + | <center><math>\vec{v}^{\,\prime}_i=\vec{v}_i-\vec{v}_A</math></center> | |
| - | + | En este sistema, la cantidad de movimiento vale | |
| - | + | <center><math>\vec{p}^{\,\prime}=\sum_im_i(\vec{v}_i-\vec{v}_A) =\vec{p}-M\vec{v}_A</math></center> | |
| - | + | y la derivada de la cantidad de movimiento en este sistema es | |
| - | <center><math>\frac{\mathrm{d}\vec{ | + | <center><math>\frac{\mathrm{d}\vec{p}^{\,\prime}}{\mathrm{d}t}=\frac{\mathrm{d}\vec{p}}{\mathrm{d}t}-M\frac{\mathrm{d}\vec{v}_A}{\mathrm{d}t}=\vec{F}_\mathrm{ext}-M\vec{a}_A</math></center> |
| + | Si el sistema de referencia móvil es inercial, <math>\vec{a}_A=\vec{0}</math>, y obtenemos el conocido teorema de la cantidad de movimiento. Si el sistema es acelerado, aparece un término de fuerza adicional, que es una fuerza ficticia, conocida como ''fuerza de inercia''. En el caso de que A sea el centro de masas, los dos términos se cancelan mutuamente y queda <math>\vec{p}^{\,\prime}</math> constante (de hecho, igual a 0, según hemos visto). | ||
[[Categoría:Mecánica de la partícula y de los sistemas (CMR)]] | [[Categoría:Mecánica de la partícula y de los sistemas (CMR)]] | ||
última version al 16:46 15 oct 2016
1 Definición
Se define la cantidad de movimiento de una partícula como el producto de su masa por su velocidad
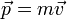
Sus dimensiones son MLT − 1 y sus unidades en el SI son  (o
(o 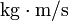 )
)
2 Teorema de la cantidad de movimiento
A partir de la definición es inmediato que

esto es, la derivada respecto al tiempo de la cantidad de movimiento es igual a la resultante de las fuerzas aplicadas sobre la partícula.
En el caso de una sola partícula, el teorema de la cantidad de movimiento no es más que la segunda ley de Newton. Este teorema cobra interés cuando se generaliza a sistemas de partículas.
3 Impulso
En ocasiones, no nos interesa tanto saber cómo cambia la cantidad de movimiento en un intervalo de tiempo infinitesimal, sino saber cuánto varía durante un cierto periodo. Supongamos una partícula que viaja libremente y por tanto con cantidad de movimiento constante 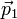 . Entonces es sometida a una fuerza
. Entonces es sometida a una fuerza 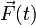 durante un intervalo entre t1 y t2 (por ejemplo, durante una colisión), a partir del cual vuelve a moverse libremente, con cantidad de movimiento constante
durante un intervalo entre t1 y t2 (por ejemplo, durante una colisión), a partir del cual vuelve a moverse libremente, con cantidad de movimiento constante 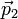 . Se trata de hallar el incremento en la cantidad de movimiento durante la colisión.
. Se trata de hallar el incremento en la cantidad de movimiento durante la colisión.
Denominamos el impulso como la integral de la fuerza respecto al tiempo en el intervalo en el que actúa
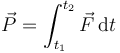
Integrando en la segunda ley de Newton obtenemos
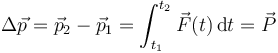
Es decir
- “El incremento de la cantidad de movimiento es igual al impulso recibido”
Esta relación, aparentemente trivial, tiene su importancia en la teoría de colisiones y de percusiones, donde se ignora el valor exacto de la fuerza, pero sí se conoce el valor del impulso.
4 Teorema de conservación de la cantidad de movimiento
De la segunda ley de Newton es inmediato que:
- “La cantidad de movimiento de una partícula permanece constante cuando la resultante de las fuerzas que actúan sobre ella es nula durante un intervalo de tiempo”
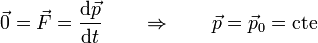
Puesto que la masa de la partícula permanece constante, si la cantidad de movimiento se conserva, la velocidad también permanece constante
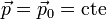

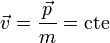
Por tanto, si la resultante de las fuerzas que actúan sobre la partícula se anula durante un intervalo de tiempo, la partícula se desplaza con un movimiento rectilíneo y uniforme durante dicho periodo.
Esto no es exactamente lo mismo que lo que dice la Primera Ley de Newton, pues esta ley habla de partícula no sometida a ninguna interacción, mientras que el teorema de conservación se refiere a una partícula sometida a diferentes fuerzas, pero tales que su resultante es nula.
Para el caso de una partícula este teorema de conservación aporta poca información nueva. Sin embargo, su extensión al caso de un sistema de partículas es extremadamente útil.
5 Conservación parcial de la cantidad de movimiento
La cantidad de movimiento es un vector, con tres componentes cartesianas. Por ello, son posibles situaciones en las que, si bien no se conserva la cantidad de movimiento en su totalidad, sí sea constante alguna de sus componentes. Concretamente:
- Si la resultante de las fuerzas que actúan sobre una partícula es en todo instante perpendicular a la dirección marcada por un vector unitario
 , fijo, entonces se conserva la componente en dicha dirección
, fijo, entonces se conserva la componente en dicha dirección
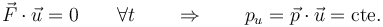
Un ejemplo típico lo tenemos en el caso del movimiento por acción del peso (tiro parabólico). Al ser éste vertical en todo instante, las componentes horizontales de la cantidad de movimiento se conservan (no así la vertical).
6 Cantidad de movimiento de un sistema de partículas
La cantidad de movimiento (o momento lineal) del sistema es la suma de las cantidades de movimiento de cada una de las partículas
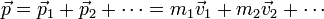
7 Relación con el centro de masas
El centro de masas de un sistema de partículas se define como un punto cuya posición es la media ponderada de las posiciones respectivas.
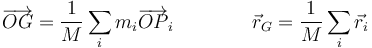
7.1 Velocidad del centro de masas
El centro de masas no es un punto fijo, sino que puede desplazarse cuando lo hacen las partículas del sistema. Obtenemos su velocidad derivando la definición respecto al tiempo
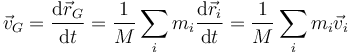
El numerador es justamente la cantidad de movimiento del sistema
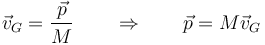
Por tanto, la cantidad de movimiento del sistema es la misma que tendría una sola partícula que concentrara la masa de todas y se moviera como el centro de masas.
8 Evolución de la cantidad de movimiento
Supongamos un sistema de partículas sometidas a fuerzas externas y también interactuantes entre sí, cumpliendo las fuerzas internas la tercera ley de Newton. En este caso, la variación en el tiempo de la cantidad de movimiento total es

esto es, la derivada de la cantidad de movimiento es la resultante de todas las fuerzas que actúan sobre las partículas del sistema. Esto es consecuencia directa de la definición, pero es poco útil pues requiere conocer también las fuerzas internas que son normalmente desconocidas. Por ello, descomponemos las fuerzas sobre cada partícula en suma de las externas y de las internas

y la derivada de la cantidad de movimiento queda

Pero, de acuerdo con la tercera ley de Newton

y análogamente para el resto de pares de partículas. Por tanto, las fuerzas internas se cancelan dos a dos y queda la expresión mucho más útil

siendo  la resultante de las fuerzas externas aplicadas, esto es
la resultante de las fuerzas externas aplicadas, esto es
- la derivada de la cantidad de movimiento es igual a la resultante de las fuerzas externas aplicadas sobre el sistema.
En términos del centro de masas, la ley de evolución de la cantidad de movimiento se escribe
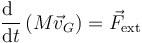
es decir:
- El centro de masas de un sistema de partículas se mueve como una sola partícula cuya masa fuera la total del sistema y que se encontrara sometida a la resultante de las fuerzas externas ejercidas sobre el sistema.
En un sistema cerrado, en el que la masa total permanece constante, la derivada de la masa es cero y obtenemos
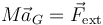
Como ejemplo tenemos el lanzamiento de un objeto. Aunque las distintas partes del objeto pueden seguir trayectorias complicadas, su CM se mueve como una partícula sometida exclusivamente a la acción del peso, es decir, describe una parábola
9 Conservación de la cantidad de movimiento
Del teorema de la cantidad de movimiento
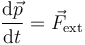
se deduce de manera inmediata que:
- En un sistema de partículas tal que la resultante de las fuerzas externas es nula durante un cierto intervalo de tiempo, la cantidad de movimiento del sistema permanece constante durante dicho intervalo
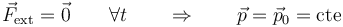
En particular:
- En un sistema de partículas sometido exclusivamente a fuerzas internas la cantidad de movimiento del sistema permanece constante
Asimismo, este teorema implica que
- El centro de masas de un sistema de partículas sometido exclusivamente a fuerzas internas describe un movimiento rectilíneo y uniforme
Por tratarse de una identidad vectorial, es posible que se conserve alguna de las componentes de la cantidad de movimiento mientras que otras son variables.
- En un sistema de partículas tal que la resultante de las fuerzas externas es perpendicular a un vector fijo
 durante un cierto intervalo de tiempo, la componente de la cantidad de movimiento del sistema en la dirección de
durante un cierto intervalo de tiempo, la componente de la cantidad de movimiento del sistema en la dirección de  permanece constante durante dicho intervalo
permanece constante durante dicho intervalo
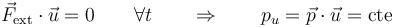
Este principio imposibilita que, por ejemplo, un grupo de aguerridos astronautas consiga desviar la trayectoria de un cometa simplemente colocando una bomba en él, ya que las fuerzas debidas a la bomba son puramente internas, y el centro de masas continuará su trayectoria inalterada, por mucho que se fragmente el asteroide.
10 Sistema de referencia del centro de masas
Una vez definida la posición del centro de masas, interesa indicar dónde están situadas las partículas respecto al CM. Esto se consigue definiendo la posición relativa
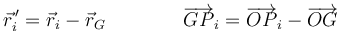
Dado que la posición del centro de masas respecto a sí mismo es evidentemente nula, se cumple
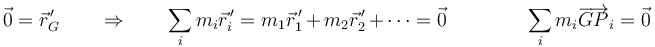
De manera análoga se define la velocidad relativa al CM
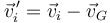
y, del mismo modo que con la posición
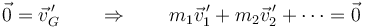
ya que el centro de masas no se mueve respecto a sí mismo.
De la relación entre cantidad de movimiento y velocidad del centro de masas se llega a que la cantidad de movimiento del sistema respecto al centro de masas es siempre nula
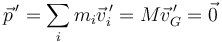
Esto permite redefinir el centro de masas como aquel punto (variable) desde el cual la cantidad de movimiento del sistema es nula en todo momento. Cuando un sistema de partículas se estudia empleando este punto como origen del sistema de referencia se dice que se está estudiando desde el sistema centro de masas.
11 Sistema de referencia móvil
El caso del sistema CM es uno particular de sistema de referencia móvil. Si consideramos un caso más general de un sistema de referencia que se traslada (sin rotar) con una velocidad 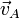 , la velocidad de las partículas respecto a este sistema es
, la velocidad de las partículas respecto a este sistema es
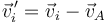
En este sistema, la cantidad de movimiento vale
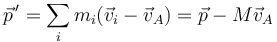
y la derivada de la cantidad de movimiento en este sistema es
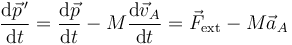
Si el sistema de referencia móvil es inercial, 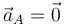 , y obtenemos el conocido teorema de la cantidad de movimiento. Si el sistema es acelerado, aparece un término de fuerza adicional, que es una fuerza ficticia, conocida como fuerza de inercia. En el caso de que A sea el centro de masas, los dos términos se cancelan mutuamente y queda
, y obtenemos el conocido teorema de la cantidad de movimiento. Si el sistema es acelerado, aparece un término de fuerza adicional, que es una fuerza ficticia, conocida como fuerza de inercia. En el caso de que A sea el centro de masas, los dos términos se cancelan mutuamente y queda 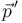 constante (de hecho, igual a 0, según hemos visto).
constante (de hecho, igual a 0, según hemos visto).






