Dinámica impulsiva vectorial (CMR)
De Laplace
(Página creada con '==Definición de percusión== ==Percusiones de reacción== ==Teorema de la cantidad de movimiento== ==Teorema del momento cinético== ==Teorema de la energía cinética== [[Cate…') |
|||
| Línea 1: | Línea 1: | ||
==Definición de percusión== | ==Definición de percusión== | ||
| + | Cuando una partícula experimenta una fuerza muy intensa (''fuerza impulsiva'') durante un breve intervalo de tiempo se dice que ha sufrido una percusión. Un típico ejemplo de percusión es una colisión entre una partícula y una pared. | ||
| + | |||
| + | Las percusiones se modelan mediante la hipótesis de una fuerza no nula que actúa solo durante un intervalo <math>\Delta t</math> de forma que se define la percusión debido a esta fuerza mediante la integral | ||
| + | |||
| + | <center><math>\vec{P}=\int_{t_1}^{t_1+\Delta t}\vec{F}\,\mathrm{d}t</math></center> | ||
| + | |||
| + | La duración de la percusión se supone infinitesimal comparada con el tiempo característico de movimiento de la partícula. Esto implica que la fuerza media <math>\vec{F}_m =\vec{P}/\Delta t</math> es gigantesca comparada con el resto de fuerzas aplicadas. Esto permite dividir la evolución de un sistema sometido a percusiones en tres fases: | ||
| + | |||
| + | * Previa a la percusión, en que la partícula actúa sometida a fuerzas aplicadas no impulsivas y su posición y velocidad evolucionan gradualmente. | ||
| + | * Durante la percusión, puede considerarse que la partícula se mueve sometida exclusivamente a las fuerzas impulsivas, ya que el resto son despreciables. Durante este breve intervalo de tiempo puede suponerse que la velocidad de la partícula experimenta un salto finito, pero que la posición de la partícula no cambia. | ||
| + | * Tras la percusión, la partícula vuelve a moverse sometida a fuerzas aplicadas no impulsivas, pero con unas condiciones iniciales que son el resultado de aplicar la percusión. | ||
| + | |||
| + | Normalmente para estudiar las percusiones no es preciso conocer el detalle de las fuerzas impulsivas (que pueden ser extremadamente complejas, como en el caso de una colisión de una pelota con una pared). Si fuera necesario, se hacen modelos como suponer que la fuerza se comporta como un pulso rectangular o un pulso gaussiano, muy estrechos. | ||
==Percusiones de reacción== | ==Percusiones de reacción== | ||
==Teorema de la cantidad de movimiento== | ==Teorema de la cantidad de movimiento== | ||
Revisión de 19:40 3 oct 2016
Contenido |
1 Definición de percusión
Cuando una partícula experimenta una fuerza muy intensa (fuerza impulsiva) durante un breve intervalo de tiempo se dice que ha sufrido una percusión. Un típico ejemplo de percusión es una colisión entre una partícula y una pared.
Las percusiones se modelan mediante la hipótesis de una fuerza no nula que actúa solo durante un intervalo Δt de forma que se define la percusión debido a esta fuerza mediante la integral
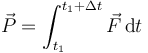
La duración de la percusión se supone infinitesimal comparada con el tiempo característico de movimiento de la partícula. Esto implica que la fuerza media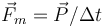 
es gigantesca comparada con el resto de fuerzas aplicadas. Esto permite dividir la evolución de un sistema sometido a percusiones en tres fases:
- Previa a la percusión, en que la partícula actúa sometida a fuerzas aplicadas no impulsivas y su posición y velocidad evolucionan gradualmente.
- Durante la percusión, puede considerarse que la partícula se mueve sometida exclusivamente a las fuerzas impulsivas, ya que el resto son despreciables. Durante este breve intervalo de tiempo puede suponerse que la velocidad de la partícula experimenta un salto finito, pero que la posición de la partícula no cambia.
- Tras la percusión, la partícula vuelve a moverse sometida a fuerzas aplicadas no impulsivas, pero con unas condiciones iniciales que son el resultado de aplicar la percusión.
Normalmente para estudiar las percusiones no es preciso conocer el detalle de las fuerzas impulsivas (que pueden ser extremadamente complejas, como en el caso de una colisión de una pelota con una pared). Si fuera necesario, se hacen modelos como suponer que la fuerza se comporta como un pulso rectangular o un pulso gaussiano, muy estrechos.
