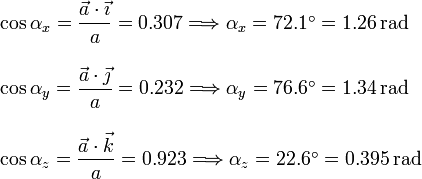Componentes cartesianas de un vector (G.I.A.)
De Laplace
(→Cosenos directores) |
(→Enunciado) |
||
| (2 ediciones intermedias no se muestran.) | |||
| Línea 1: | Línea 1: | ||
== Enunciado == | == Enunciado == | ||
| - | + | Calcule las componentes cartesianas de un vector <math>\vec{a}</math> con módulo de 13.0 unidades que forma un | |
| - | ángulo <math>\gamma=22.6^{\circ}</math> con el eje <math> | + | ángulo <math>\gamma=22.6^{\circ}</math> con el eje <math>OZ</math> y cuya proyección en el plano <math>OXY</math> forma un ángulo |
| - | <math>\alpha=37.0^{\circ}</math> con el eje <math> | + | <math>\alpha=37.0^{\circ}</math> con el eje <math>OX</math>. Calcule también los ángulos con los ejes <math>OX</math> y <math>OY</math>. |
== Solución == | == Solución == | ||
| Línea 51: | Línea 51: | ||
[[Categoría:Vectores libres|0]] | [[Categoría:Vectores libres|0]] | ||
[[Categoría:Física I (G.I.A.)]] | [[Categoría:Física I (G.I.A.)]] | ||
| + | [[Categoría:Física I (G.I.T.I.)]] | ||
| + | [[Categoría:Física I (G.I.C.)]] | ||
última version al 19:20 29 sep 2016
1 Enunciado
Calcule las componentes cartesianas de un vector 
con módulo de 13.0 unidades que forma un
ángulo 
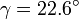con el eje OZ y cuya proyección en el plano OXY forma un ángulo
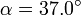con el eje OX. Calcule también los ángulos con los ejes OX y OY.
2 Solución
La figura muestra el vector y su orientación respecto a los ejes. La componente sobre el eje Z se obtiene proyectando ortogonalmente el vector sobre el eje
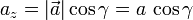
La proyección sobre el plano XY es
La componente ax del vector se obtiene proyectando a su vez la proyección del vector sobre el X usando el ángulo α
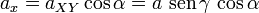
Y la componente ay usando el seno del ángulo α
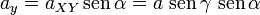
Finalmente, la expresión del vector en la base cartesiana es
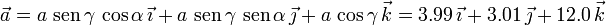
2.1 Cosenos directores
Calcular los ángulos que el vector forma con los ejes es calcular sus cosenos directores. Para ellos usamos el producto escalar del vector con un vector unitario paralelo a cada uno de los ejes. Tenemos
