Cinemática de la partícula (CMR)

De Laplace

(Diferencias entre revisiones)

Revisión de 21:57 16 sep 2016

1 Introducción

2 Sistemas de referencia

En Mecánica Clásica se considera que el espacio es euclídeo, es decir, que podemos construir sistemas de referencia cartesianos que se extienden a todo el espacio.

Los puntos del espacio pueden etiquetarse mediante letras, O, P, Q,… Sin embargo, para operar con ellos, es conveniente emplear coordenadas, que no son más que etiquetas numéricas que identifican cada punto de forma unívoca.

Existen muchos sistemas de coordenadas posibles. Las más sencillas son las coordenadas cartesianas

Dado un punto del espacio, O, que tomamos como origen de coordenadas, tomamos tres planos que pasan por dicho punto y que sean ortogonales entre sí, que denominaremos XY, XZ e YZ. Definimos entonces las coordenadas cartesianas de cualquier otro punto como las distancias (con signo), $x$ , $y$ , $z$ a estos planos coordenados ( $x$ la distancia al YZ, $y$ al XZ, y $z$ al XY).

Los planos se cortan en tres rectas, también ortogonales entre sí, que denominamos ejes de coordenadas OX, OY y OZ (o simplemente X, Y y Z).

Los vectores unitarios tangentes a estos ejes forman una base ortonormal que denotamos como $\{\vec{\imath},\vec{\jmath},\vec{k}\}$ .

Por ser ortonormales, verifican

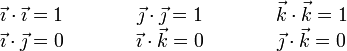
$\begin{array}{ccccc} \vec{\imath}\cdot\vec{\imath}=1 & \qquad & \vec{\jmath}\cdot\vec{\jmath}=1 & \qquad & \vec{k}\cdot\vec{k}=1 \\ \vec{\imath}\cdot\vec{\jmath}=0 & \qquad & \vec{\imath}\cdot\vec{k}=0 & \qquad & \vec{\jmath}\cdot\vec{k}=0 \end{array}$

o, en forma de tabla:

$\cdot\,$	$\vec{\imath}$	$\vec{\jmath}$	$\vec{k}$
$\vec{\imath}$	1	0	0
$\vec{\jmath}$	0	1	0
$\vec{k}$	0	0	1

Esta base canónica es además dextrógira, esto es, verifica la regla de la mano derecha cuando los vectores se colocan en el orden $\{\vec{\imath},\vec{\jmath},\vec{k}\}$ . Empleando el producto vectorial, esto se expresa

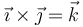
$\vec{\imath} \times \vec{\jmath} = \vec{k}$

y análogamente para el resto de productos: positivo si se gira en sentido antihorario y negativo si se va en sentido horario en la figura. En forma de tabla:

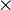
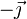
$\times\,$	$\vec{\imath}$	$\vec{\jmath}$	$\vec{k}$
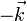
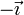
$\vec{\imath}$	$\vec{0}$	$\vec{k}$	$-\vec{\jmath}$
$\vec{\jmath}$	$-\vec{k}$	$\vec{0}$	$\vec{\imath}$
$\vec{k}$	$\vec{\jmath}$	$-\vec{\imath}$	$\vec{0}$

En términos de esta base, cualquier vector podrá escribirse como una combinación lineal

$\vec{A}=A_x\vec{\imath}+A_y\vec{\jmath}+A_z\vec{k}$

La posición de cualquier punto P puede expresarse mediante su vector de posición, que es aquél que tiene como origen el de coordenadas y como extremo el punto P (es, por tanto, un vector ligado)

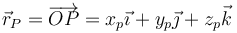
$\vec{r}_P =\overrightarrow{OP} =x_p\vec{\imath}+y_p\vec{\jmath}+z_p\vec{k}$

La posición relativa del punto Q respecto al punto P la da el vector que tiene por origen P y por extremo Q. Es inmediato obtener las componentes de este vector en la base cartesiana, conocidas las coordenadas cartesianas del origen y del extremo. Basta restarle las primeras a las segundas. Si $P (x p, y p, z p)$ y $Q (x q, y q, z q)$ , el vector 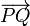$\overrightarrow{PQ}$ es:

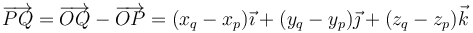
$\overrightarrow{PQ}=\overrightarrow{OQ}-\overrightarrow{OP}= (x_q-x_p)\vec{\imath}+(y_q-y_p)\vec{\jmath}+(z_q-z_p)\vec{k}$

3 Posición, trayectoria y ley horaria

Una partícula material es, en mecánica, un modelo en el que un objeto se considera con masa, pero ocupando solo un punto del espacio. Se aplica al estudio de cuerpos cuyas dimensiones son mucho menores que las distancias que recorre o a puntos particulares de cuerpos extensos, como puede ser el centro de masas de un sistema.

3.1 Posición y desplazamiento

En su movimiento por el espacio, la posición de una partícula va cambiando de forma continua

$\vec{r}_P(t)= x(t)\vec{\imath}+y(t)\vec{\jmath}+z(t)\vec{k}$

aunque usualmente no se indica de forma explícita la dependencia con el tiempo.

Cuando la posición de una partícula se da de esta forma se dice que tenemos la ecuación horaria de su movimiento.

El desplzamiento de una partícula en un intervalo es la diferencia vectorial entre sus posiciónes

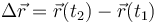
$\Delta \vec{r}=\vec{r}(t_2)-\vec{r}(t_1)$

Cuando este desplazamiento es muy pequeño comparado con las distancias típicas recorridas, se dice que tenemos un desplazamiento diferencial, 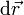$\mathrm{d}\vec{r}$ .

3.2 Trayectoria

A la curva que describe la partícula en su movimiento se la denomina la trayectoria de la partícula.

Una misma trayectoria puede ser escrita por una infinitud de ecuaciones horarias diferentes, dependiendo del ritmo con el que recorra.

Para identificar una trayectoria independientemente del tiempo se suele describir la curva en forma paramétrica

$\vec{r}_P(\theta)= x(\theta)\vec{\imath}+y(\theta)\vec{\jmath}+z(\theta)\vec{k}$

siendo θ una variable continua que identifica de forma unívoca los puntos de la curva.

De entre los diferentes parámetros posibles, destaca el llamado parámetro arco o parámetro natural, $s$ , que mide la distancia sobre la curva (en el caso de una carretera serían los puntos kilométricos). El parámetro arco se obtiene sumando las distancias diferenciales a lo largo de la trayectoria

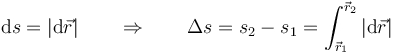
$\mathrm{d}s=\left|\mathrm{d}\vec{r}\right|\qquad\Rightarrow\qquad \Delta s=s_2-s_1=\int_{\vec{r}_1}^{\vec{r}_2}\left|\mathrm{d}\vec{r}\right|$

3.3 Ley horaria

Cuando se tiene la trayectoria parametrizada en términos de la distancia medida sobre la curva la descripción se completa indicando cómo cambia esta variable con el tiempo. Esta dependencia temporal se conoce como ley horaria:

$s = s(t)\,$

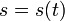
En el ejemplo de un coche que va de Sevilla a Granada, la ley horaria sería la hora a la que pasó por cada punto del camino sin prestar atención si en ese punto en concreto la carretera va hacia el sur o hacia el este.

Según esto, las ecuaciones horarias del movimiento pueden descomponerse en la trayectoria por un lado y la ley horaria por otro:

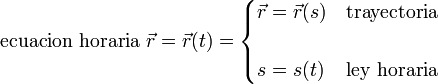
$\mbox{ecuacion horaria}\ \vec{r}=\vec{r}(t)=\begin{cases}\vec{r}=\vec{r}(s) & \mbox{trayectoria}\\ & \\ s=s(t)& \mbox{ley horaria}\end{cases}$

Si en lugar del parámetro arco, se describe la trayectoria con otra variable también se denomina ley horaria a la dependencia de esta variable con el tiempo. Así, en general:

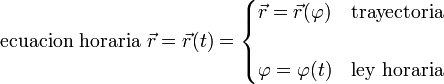
$\mbox{ecuacion horaria}\ \vec{r}=\vec{r}(t)=\begin{cases}\vec{r}=\vec{r}(\varphi) & \mbox{trayectoria}\\ & \\ \varphi=\varphi(t)& \mbox{ley horaria}\end{cases}$

4 Velocidad

Se define la velocidad media en un intervalo de tiempo como el cociente entre el desplzamiento realizado y el intervalo de tiempo empleado en realizarlo.

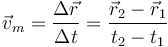
$\vec{v}_m=\frac{\Delta\vec{r}}{\Delta t}=\frac{\vec{r}_2-\vec{r}_1}{t_2-t_1}$

La velocidad instantánea de la partícula es el límite de la velocidad media cuando el intervalo de tiempo es muy pequeño

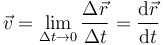
$\vec{v}=\lim_{\Delta t\to 0}\frac{\Delta\vec{r}}{\Delta t} = \frac{\mathrm{d}\vec{r}}{\mathrm{d}t}$

Es decir, la velocidad instantánea es la derivada de la posición respecto al tiempo. En Física, las derivadas respecto al tiempo suelen representarse con un punto sobre la magnitud

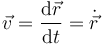
$\vec{v}= \frac{\mathrm{d}\vec{r}}{\mathrm{d}t}=\dot{\vec{r}}$

Si conocemos la velocidad instantánea a lo largo de un intervalo podemos calcular la posición como función del tiempo

$\vec{r}(t)=\vec{r}_0+\int_0^t \vec{v}\,\mathrm{d}t$

4.1 Vector tangente

El vector velocidad va en la dirección tangente a la trayectoria. Esto permite definir el unitario tangente

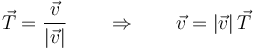
$\vec{T}=\frac{\vec{v}}{\left|\vec{v}\right|}\qquad\Rightarrow\qquad \vec{v}=\left|\vec{v}\right| \vec{T}$

4.2 Rapidez y distancia recorrida

Al módulo de la velocidad se lo denomina rapidez o celeridad de la partícula. Mide el ritmo con el que se recorre la tryectoria y como tal se relaciona directamente con el parámetro arco

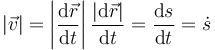
$\left|\vec{v}\right|= \left|\frac{\mathrm{d}\vec{r}}{\mathrm{d}t}\right| \frac{\left|\mathrm{d}\vec{r}\right|}{\mathrm{d}t}=\frac{\mathrm{d}s}{\mathrm{d}t}=\dot{s}$

Esto permite determinar la distancia recorrida en un intervalo de tiempo dado

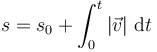
$s = s_0+\int_0^t \left|\vec{v}\right|\,\mathrm{d}t$

4.3 Componentes de la velocidad

En un sistema de referencia fijo, los vectores de la base cartesiana son constantes, por lo que

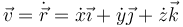
$\vec{v}=\dot{\vec{r}}=\dot{x}\vec{\imath}+\dot{y}\vec{\jmath}+\dot{z}\vec{k}$

es decir, las componentes de la velocidad son las derivadas de las componentes de la posición.

4.4 Velocidad en función de parámetros

Si la posición no está dada explícitamente en función del tiempo, sino que conocemos la trayectoria en función de un parámetro θ para hallar la velocidad es preciso aplicar la regla de la cadena

$\vec{v}=\frac{\mathrm{d}\vec{r}}{\mathrm{d}t}=\frac{\mathrm{d}\vec{r}}{\mathrm{d}\theta}\,\frac{\mathrm{d}\theta}{\mathrm{d}t}=\frac{\mathrm{d}\vec{r}}{\mathrm{d}\theta}\,\dot{\theta}$

A menudo, la posición no se indica en función de las coordenadas cartesianas, sino como función de 2 o más variables, θ, φ…. En ese caso, se generaliza la expresión anterior

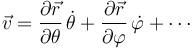
$\vec{v}=\frac{\partial\vec{r}}{\partial \theta}\, \dot{\theta}+\frac{\partial\vec{r}}{\partial \varphi}\, \dot{\varphi}+\cdots$

Si denominamos a las diferentes variables como 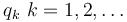$q_k\ k=1,2,\ldots$ la expresión anterior se escribe

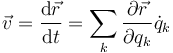
$\vec{v}=\frac{\mathrm{d}\vec{r}}{\mathrm{d}t}=\sum_k \frac{\partial\vec{r}}{\partial q_k}\dot{q}_k$

En ocasiones, la posición se expresa como función del tiempo y de una variable (dependiente implícitamente del tiempo). En ese caso, aplicamos que la derivada del tiempo respecto a sí mismo vale 1 (la velocidad del tiempo es un segundo por segundo) y queda

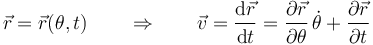
$\vec{r}=\vec{r}(\theta,t)\qquad\Rightarrow\qquad \vec{v}= \frac{\mathrm{d}\vec{r}}{\mathrm{d}t}=\frac{\partial\vec{r}}{\partial \theta}\, \dot{\theta}+\frac{\partial\vec{r}}{\partial t}$

Nótese la diferencia entre la derivada total (d) y la parcial (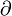 $\partial$ ).

Si depende de varias variables y del tiempo queda la fórmula general

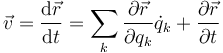
$\vec{v}=\frac{\mathrm{d}\vec{r}}{\mathrm{d}t}=\sum_k \frac{\partial\vec{r}}{\partial q_k}\dot{q}_k+\frac{\partial\vec{r}}{\partial t}$

5 Aceleración

5.1 Definición

Se define la aceleración instantánea como la derivada de la velocidad respecto al tiempo

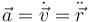
$\vec{a}=\dot{\vec{v}}=\ddot{\vec{r}}$

En una base fija, las componentes de la aceleración son las derivadas temporales de las componentes de la velocidad (y la segunda derivada de las de la posición)

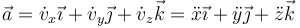
$\vec{a}=\dot{v}_x\vec{\imath}+\dot{v}_y\vec{\jmath}+\dot{v}_z\vec{k}=\ddot{x}\vec{\imath}+\ddot{y}\vec{\jmath}+\ddot{z}\vec{k}$

5.2 Componentes intrínsecas

Derivando la expresión de la velocidad como producto de la rapidez y el vector tangente

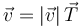
$\vec{v}=\left|\vec{v}\right| \vec{T}$

queda

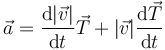
$\vec{a}=\frac{\mathrm{d}|\vec{v}|}{\mathrm{d}t}\vec{T}+|\vec{v}|\frac{\mathrm{d}\vec{T}}{\mathrm{d}t}$

El primero de los dos sumandos es paralelo al vector tangente y a la velocidad. El segundo es ortogonal a $\vec{T}$ , por ser éste un vector de módulo constante. Por tanto, la aceleración se puede escribir como suma de una aceleración tangencial, responsable del cambio en la rapidez, y de una aceleración normal, asociada al cambio en la dirección del movimiento.

$\vec{a}_t=\frac{\mathrm{d}|\vec{v}|}{\mathrm{d}t}\vec{T}\qquad\qquad \vec{a}_n=|\vec{v}|\frac{\mathrm{d}\vec{T}}{\mathrm{d}t}$

Estas dos componentes pueden también hallarse proyectando sobre la velocidad

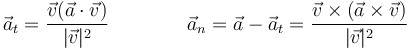
$\vec{a}_t=\frac{\vec{v}(\vec{a}\cdot\vec{v})}{|\vec{v}|^2}\qquad\qquad\vec{a}_n= \vec{a}-\vec{a}_t=\frac{\vec{v}\times(\vec{a}\times\vec{v})}{|\vec{v}|^2}$

5.3 Triedro de Frenet

Como hemos visto, a partir de la velocidad puede definirse un unitario tangente a la trayectoria

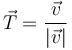
$\vec{T}=\frac{\vec{v}}{\left|\vec{v}\right|}$

y a partir de la aceleración normal podemos definir un vector unitario normal a la trayectoria

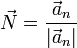
$\vec{N}=\frac{\vec{a}_n}{|\vec{a}_n|}$

Este vector es siempre ortogonal a la trayectoria y hacia adentro de las curvas que describe.

Completamos un triedro (denominado triedro de $F r e n e t$ ) mediante el producto de estos dos, obteniendo el vector binormal

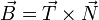
$\vec{B}=\vec{T}\times\vec{N}$

Cualquier vector puede expresarse como cominación lineal de este triedro

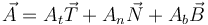
$\vec{A}=A_t\vec{T}+A_n\vec{N}+A_b\vec{B}$

En particular

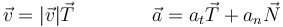
$\vec{v}=|\vec{v}|\vec{T}\qquad\qquad \vec{a}=a_t\vec{T}+a_n\vec{N}$

A diferencia de la base cartesiana, el triedro de Frenet es una función del tiempo, ya que se desplaza y gira con la partícula en su movimiento. Por ello, cualquier derivada respecto al tiempo deberá tener en cuenta las derivadas de estos vectores.

5.4 Curvatura

La curvatura de una trayectoria mide como cambia la dirección de esta. Se define a partir de la derivada del vector tangente como

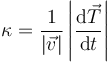
$\kappa = \frac{1}{|\vec{v}|}\left|\frac{\mathrm{d}\vec{T}}{\mathrm{d}t}\right|$

La inversa de la curvatura es el denominado radio de curvatura

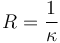
$R=\frac{1}{\kappa}$

de forma que la aceleración normal puede escribirse en la forma

$\vec{a}_n=\frac{|\vec{v}|^2}{R}\vec{N}$

El centro de curvatura se define como el punto móvil

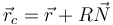
$\vec{r}_c=\vec{r}+R\vec{N}$

Este punto es el centro instantáneo de la circunferencia que más se aproxima a la trayectoria en cada posición de ésta.

6 Casos particulares

6.1 Movimiento uniforme

El movimiento de una partícula se dice uniforme cuando su rapidez es constante duante un cierto intervalo de tiempo

$\left|\vec{v}\right| = \mathrm{cte}\qquad\Leftrightarrow\qquad \mbox{mov. uniforme}$

Esta definición es equivalente a que:

La aceleración tangencial es nula durante todo ese intervalo.
La aceleración es ortogonal a la velocidad en ese periodo de tiempo

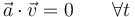
$\vec{a}\cdot\vec{v}=0\qquad\forall t$

6.2 Movimiento rectilíneo

Un movimiento es rectilíneo en un intervalo de tiempo cuando su trayectoria en dicho intervalo es una recta. Esto ocurre si el vector tangente mantiene la misma dirección

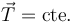
$\vec{T}=\mathrm{cte.}$

para ser precisos, puede invertir su sentido en instantes concretos, como ocurre en un movimiento armónico simple.

Esta condición equivale a que

La aceleración normal es nula en dicho intervalo
La aceleración es paralela a la velocidad

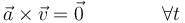
$\vec{a}\times\vec{v}=\vec{0}\qquad\qquad \forall t$

La curvatura de la trayectoria es nula

$\kappa=0\qquad\qquad \forall t$

El radio de curvatura tiende a infinito.

Una manera de identificar un movimiento rectilíneo es comprobar si su ecuación horaria es de la forma

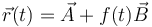
$\vec{r}(t)=\vec{A}+f(t)\vec{B}$

con $\vec{A}$ y $\vec{B}$ vectores constantes.

Si el movimiento es rectilíneo y uniforme, la velocidad de la partícula es constante

$\left\{\begin{array}{rlc}|\vec{v}|&=&\mathrm{cte} \\ \vec{T}&=&\mathrm{cte}\end{array}\right.\qquad\Leftrightarrow\qquad \vec{v}=|\vec{v}|\vec{T}=\mathrm{cte}$

o, dicho de otra forma, si la aceleración tangencial y la normal son ambs nulas, el vector aceleración es nulo.

6.3 Movimiento plano

Movimiento plano de una partícula es aquel que en todo momento de un intervalo se encuentra contenido en un plano. Si A es un punto de este plano y $\vec{B}$ es un vector normal a él, debe cumplirse la ecuación vectorial

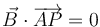
$\vec{B}\cdot\overrightarrow{AP}=0$

o, empleando los vectores de posición

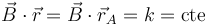
$\vec{B}\cdot\vec{r}=\vec{B}\cdot\vec{r}_A=k=\mathrm{cte}$

Alternativamente, un movimiento es plano si puede escribirse en la forma

$\vec{r}(t)=\vec{A}+f(t)\vec{V}_1+g(t)\vec{V}_2$

con $\vec{A}$ , $\vec{V}_1$ y $\vec{V}_2$ vectores constantes.

6.4 Movimiento circular

@@ Línea 316: / Línea 316: @@
 ===Movimiento plano===
+Movimiento plano de una partícula es aquel que en todo momento de un intervalo se encuentra contenido en un plano. Si A es un punto de este plano y <math>\vec{B}</math> es un vector normal a él, debe cumplirse la ecuación vectorial
+<center><math>\vec{B}\cdot\overrightarrow{AP}=0</math></center>
+o, empleando los vectores de posición
+<center><math>\vec{B}\cdot\vec{r}=\vec{B}\cdot\vec{r}_A=k=\mathrm{cte}</math></center>
+Alternativamente, un movimiento es plano si puede escribirse en la forma
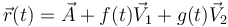
+<center><math>\vec{r}(t)=\vec{A}+f(t)\vec{V}_1+g(t)\vec{V}_2</math></center>
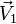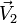+con <math>\vec{A}</math>, <math>\vec{V}_1</math> y <math>\vec{V}_2</math> vectores constantes.
 ===Movimiento circular===
 [[Categoría:Mecánica de la partícula y de los sistemas (CMR)]]