Cinemática de la partícula (CMR)
De Laplace
(Página creada con '==Introducción== ==Sistemas de referencia== ==Posición, trayectoria y ley horaria== ==Velocidad== ==Aceleración== [[Categoría:Mecánica de la partícula y de los sistemas (C…') |
|||
| Línea 1: | Línea 1: | ||
==Introducción== | ==Introducción== | ||
==Sistemas de referencia== | ==Sistemas de referencia== | ||
| + | En Mecánica Clásica se considera que el espacio es euclídeo, es decir, que podemos construir sistemas de referencia cartesianos que se extienden a todo el espacio. | ||
| + | |||
| + | Los puntos del espacio pueden etiquetarse mediante letras, O, P, Q,… Sin embargo, para operar con ellos, es conveniente emplear ''coordenadas'', que no son más que etiquetas numéricas que identifican cada punto de forma unívoca. | ||
| + | |||
| + | [[Archivo:car-def-flecha.png|right]] | ||
| + | |||
| + | Existen muchos sistemas de coordenadas posibles. Las más sencillas son las ''coordenadas cartesianas'' | ||
| + | |||
| + | Dado un punto del espacio, ''O'', que tomamos como '''origen de coordenadas''', tomamos tres planos que pasan por dicho punto y que sean ortogonales entre sí, que denominaremos XY, XZ e YZ. Definimos entonces las coordenadas cartesianas de cualquier otro punto como las distancias (con signo), <math>x</math>, <math>y</math>, <math>z</math> a estos planos coordenados (<math>x</math> la distancia al YZ, <math>y</math> al XZ, y <math>z</math> al XY). | ||
| + | |||
| + | Los planos se cortan en tres rectas, también ortogonales entre sí, que denominamos ''ejes de coordenadas'' OX, OY y OZ (o simplemente X, Y y Z). | ||
| + | |||
| + | Los vectores unitarios tangentes a estos ejes forman una base ortonormal que denotamos como <math>\{\vec{\imath},\vec{\jmath},\vec{k}\}</math>. | ||
| + | |||
| + | Por ser ortonormales, verifican | ||
| + | |||
| + | <center><math>\begin{array}{ccccc} | ||
| + | \vec{\imath}\cdot\vec{\imath}=1 & \qquad & \vec{\jmath}\cdot\vec{\jmath}=1 & \qquad & \vec{k}\cdot\vec{k}=1 \\ | ||
| + | \vec{\imath}\cdot\vec{\jmath}=0 & \qquad & \vec{\imath}\cdot\vec{k}=0 & \qquad & \vec{\jmath}\cdot\vec{k}=0 | ||
| + | \end{array}</math></center> | ||
| + | |||
| + | o, en forma de tabla: | ||
| + | |||
| + | <center> | ||
| + | {| class="bordeado" | ||
| + | |- | ||
| + | ! <math>\cdot\,</math> | ||
| + | ! <math>\vec{\imath}</math> | ||
| + | ! <math>\vec{\jmath}</math> | ||
| + | ! <math>\vec{k}</math> | ||
| + | |- | ||
| + | ! <math>\vec{\imath}</math> | ||
| + | | 1 | ||
| + | | 0 | ||
| + | | 0 | ||
| + | |- | ||
| + | ! <math>\vec{\jmath}</math> | ||
| + | | 0 | ||
| + | | 1 | ||
| + | | 0 | ||
| + | |- | ||
| + | ! <math>\vec{k}</math> | ||
| + | | 0 | ||
| + | | 0 | ||
| + | | 1 | ||
| + | |} | ||
| + | </center> | ||
| + | |||
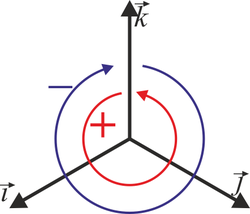
| + | Esta base canónica es además dextrógira, esto es, verifica la regla de la mano derecha cuando los vectores se colocan en el orden <math>\{\vec{\imath},\vec{\jmath},\vec{k}\}</math>. Empleando el producto vectorial, esto se expresa | ||
| + | |||
| + | [[Archivo:producto-vectoria-base-canonica.png|250px|right]] | ||
| + | |||
| + | <center><math>\vec{\imath} \times \vec{\jmath} = \vec{k}</math></center> | ||
| + | |||
| + | y análogamente para el resto de productos: positivo si se gira en sentido antihorario y negativo si se va en sentido horario en la figura. En forma de tabla: | ||
| + | |||
| + | <center> | ||
| + | {| class="bordeado" | ||
| + | |- | ||
| + | ! <math>\times\,</math> | ||
| + | ! <math>\vec{\imath}</math> | ||
| + | ! <math>\vec{\jmath}</math> | ||
| + | ! <math>\vec{k}</math> | ||
| + | |- | ||
| + | ! <math>\vec{\imath}</math> | ||
| + | | <math>\vec{0}</math> | ||
| + | | <math>\vec{k}</math> | ||
| + | | <math>-\vec{\jmath}</math> | ||
| + | |- | ||
| + | ! <math>\vec{\jmath}</math> | ||
| + | | <math>-\vec{k}</math> | ||
| + | | <math>\vec{0}</math> | ||
| + | | <math>\vec{\imath}</math> | ||
| + | |- | ||
| + | ! <math>\vec{k}</math> | ||
| + | | <math>\vec{\jmath}</math> | ||
| + | | <math>-\vec{\imath}</math> | ||
| + | | <math>\vec{0}</math> | ||
| + | |} | ||
| + | </center> | ||
| + | |||
==Posición, trayectoria y ley horaria== | ==Posición, trayectoria y ley horaria== | ||
==Velocidad== | ==Velocidad== | ||
==Aceleración== | ==Aceleración== | ||
[[Categoría:Mecánica de la partícula y de los sistemas (CMR)]] | [[Categoría:Mecánica de la partícula y de los sistemas (CMR)]] | ||
Revisión de 15:44 14 sep 2016
Contenido |
1 Introducción
2 Sistemas de referencia
En Mecánica Clásica se considera que el espacio es euclídeo, es decir, que podemos construir sistemas de referencia cartesianos que se extienden a todo el espacio.
Los puntos del espacio pueden etiquetarse mediante letras, O, P, Q,… Sin embargo, para operar con ellos, es conveniente emplear coordenadas, que no son más que etiquetas numéricas que identifican cada punto de forma unívoca.
Existen muchos sistemas de coordenadas posibles. Las más sencillas son las coordenadas cartesianas
Dado un punto del espacio, O, que tomamos como origen de coordenadas, tomamos tres planos que pasan por dicho punto y que sean ortogonales entre sí, que denominaremos XY, XZ e YZ. Definimos entonces las coordenadas cartesianas de cualquier otro punto como las distancias (con signo), x, y, z a estos planos coordenados (x la distancia al YZ, y al XZ, y z al XY).
Los planos se cortan en tres rectas, también ortogonales entre sí, que denominamos ejes de coordenadas OX, OY y OZ (o simplemente X, Y y Z).
Los vectores unitarios tangentes a estos ejes forman una base ortonormal que denotamos como  .
.
Por ser ortonormales, verifican
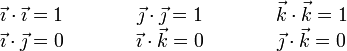
o, en forma de tabla:

| 
| 
| 
|
|---|---|---|---|

| 1 | 0 | 0 |

| 0 | 1 | 0 |

| 0 | 0 | 1 |
Esta base canónica es además dextrógira, esto es, verifica la regla de la mano derecha cuando los vectores se colocan en el orden  . Empleando el producto vectorial, esto se expresa
. Empleando el producto vectorial, esto se expresa
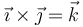
y análogamente para el resto de productos: positivo si se gira en sentido antihorario y negativo si se va en sentido horario en la figura. En forma de tabla:
| 
| 
| 
|
|---|---|---|---|

| 
| 
| 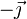
|

| 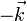
| 
| 
|

| 
| 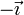
| 
|