Moneda que va y vuelve
De Laplace
| Línea 10: | Línea 10: | ||
==Aceleraciones y velocidades== | ==Aceleraciones y velocidades== | ||
Este problema es esencialmente el mismo que el de “[[Deslizamiento_y_rodadura_de_un_disco|Deslizamiento y rodadura de un disco]]”. | Este problema es esencialmente el mismo que el de “[[Deslizamiento_y_rodadura_de_un_disco|Deslizamiento y rodadura de un disco]]”. | ||
| + | |||
| + | La moneda se mueve sometida a tres fuerzas: | ||
| + | |||
| + | * Su peso, <math>m\vec{g}=-mg\vec{\jmath}</math>. | ||
| + | * La fuerza de reacción normal, <math>\vec{F}_n=F_n\vec{\jmath}</math>. | ||
| + | * La fuerza de rozamiento por deslizamiento, <math>\vec{F}_r=-F_r\vec{\imath}</math>. | ||
| + | |||
| + | Estas fuerzas producen tanto aceleración del CM como aceleración angular del disco, | ||
==Velocidad del punto de contacto== | ==Velocidad del punto de contacto== | ||
==Condición de retroceso== | ==Condición de retroceso== | ||
| - | |||
Revisión de 10:26 13 sep 2016
Contenido |
1 Enunciado
Un conocido experimento casero es el de lanzar una moneda rodando y deslizando por un suelo horizontal y conseguir que retorne al lanzador. Supongamos que disponemos de una moneda de 2 euros (25.75 mm de diámetro, 8.50 g de masa) que podemos suponer un disco homogéneo. Se encuentra en posición vertical sobre una superficie horizontal en la que el coeficiente de rozamiento (estático y dinámico) vale μ = 0.05. Se lanza horizontalmente con una velocidad inicial de su centro G, 
m⁄s y una cierta velocidad angular inicial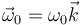 
que habrá que determinar, de forma que en el punto de contacto A la moneda rueda y desliza.
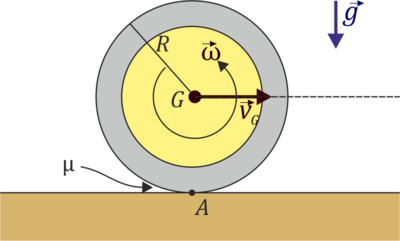
La moneda realiza un movimiento plano en todo momento.
- Determine la aceleración lineal del centro,
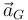y la aceleración angular de la moneda, 
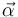. A partir de ellas, calcule la velocidad lineal del centro y la velocidad angular del disco como funciones del tiempo.
- Calcule la velocidad de la moneda en el punto de contacto A como función del tiempo. Determine el instante en el que la moneda deja de deslizar y comienza a rodar sin deslizar. ¿Cuál es la velocidad del centro G del disco en ese instante?
- Determine el mínimo valor de ω0 por encima del cual la moneda retrocede y vuelve al lanzador. Para este valor de ω0, ¿Qué distancia recorre el centro de la moneda hasta que ésta deja de rodar?
Tómese g = 9.81ms2.
2 Aceleraciones y velocidades
Este problema es esencialmente el mismo que el de “Deslizamiento y rodadura de un disco”.
La moneda se mueve sometida a tres fuerzas:
- Su peso,
.
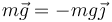- La fuerza de reacción normal,
.
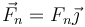- La fuerza de rozamiento por deslizamiento,
.
Estas fuerzas producen tanto aceleración del CM como aceleración angular del disco,
