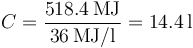Frigorífico alimentado por un generador
De Laplace
(→Enunciado) |
|||
| Línea 7: | Línea 7: | ||
==Potencia== | ==Potencia== | ||
| + | Para mantener el estado estacionario, el calor que entra en la cámara frigorífica desde el exterior debe ser compensado por el que sale de ella gracias a la máquina frigorífica | ||
| + | |||
| + | <center><math>\dot{Q}^{CF}_\mathrm{out}=\dot{Q}^R_\mathrm{in}}</math></center> | ||
| + | |||
| + | Por tanto, el flujo de calor que entra en la máquina frigorífica es | ||
| + | |||
| + | <center><math>\dot{Q}^R_\mathrm{in}=5.4\,\mathrm{kWt}</math></center> | ||
| + | |||
| + | El coeficiente de desempeño de un refrigerador, por definición, es igual a | ||
| + | |||
| + | <center><math>\mathrm{COP}_R=\frac{\dot{Q}^R_\mathrm{in}}{\dot{W}_\mathrm{in}}</math></center> | ||
| + | |||
| + | y por tanto, la potencia necesaria para hacer funcionar el refrigerador es | ||
| + | |||
| + | <center><math>\dot{W}^{R}_\mathrm{in}=\frac{\dot{Q}^R_\mathrm{in}}{\mathrm{COP}_R}=\frac{5.4}{3}\mathrm{kW}=1.8\,\mathrm{kW}</math></center> | ||
| + | |||
==Flujo de calor== | ==Flujo de calor== | ||
| + | La potencia del apartado anterior es suministrada por un generador | ||
| + | |||
| + | <center><math>\dot{W}^{R}_\mathrm{in}=\dot{W}^{MT}_\mathrm{out}</math></center> | ||
| + | |||
| + | siendo el rendimiento un 30%, por tanto, | ||
| + | |||
| + | <math>\frac{\dot{W}^{MT}_\mathrm{out}}{\dot{Q}^{MT}_\mathrm{in}}=0.30\qquad\Rightarrow\qquad \dot{Q}^{MT}_\mathrm{in}=\frac{1.8}{0.3}=6.0\,\mathrm{kW}</math> | ||
| + | |||
==Consumo de combustible== | ==Consumo de combustible== | ||
| + | El resultado anterior indica que se precisan 6 kJ/s de calor. A lo largo de un día se necesitarán | ||
| + | |||
| + | <center><math>Q^{MT}_\mathrm{in}=6\mathrm{kW}\times 24\times 3600\,\mathrm{s} = 518.4\,\mathrm{MJ}</math></center> | ||
| + | |||
| + | Si cada litro aporta 36MJ el consumo será | ||
| + | |||
| + | <center><math>C = \frac{518.4\,\mathrm{MJ}}{36\,\mathrm{MJ}/\mathrm{l}}=14.4\,\mathrm{l}</math></center> | ||
| + | |||
==Producción de entropía== | ==Producción de entropía== | ||
Revisión de 19:53 9 sep 2016
Contenido |
1 Enunciado
En una casa de campo se tiene un frigorífico cuya temperatura interior es de 3 °C siendo la exterior de 27 °C. En el estado estacionario, a través de las paredes escapa un flujo de calor de 5.4kWt. El COPR del frigorífico vale 3. Para hacer funcionar la nevera se usa un generador de gasoil que tiene un rendimiento del 30% y en el cual el combustible alcanza la temperatura de 1500K. El poder calorífico del gasoil empleado es de 36 MJ por cada litro de combustible.
- Calcule el flujo de trabajo (potencia) necesario para mantener en funcionamiento la máquina frigorífica.
- Halle el flujo de calor que debe producirse en la combustión dentro del generador para generar la potencia que necesita la máquina frigorífica.
- Calcule el consumo de gasoil, en litros, a lo largo de un día para mantener el sistema en funcionamiento.
- Determine la producción de entropía por segundo en el generador, en la máquina frigorífica del refrigerador y en la cámara frigorífica, así como la producción total de entropía por segundo.
2 Potencia
Para mantener el estado estacionario, el calor que entra en la cámara frigorífica desde el exterior debe ser compensado por el que sale de ella gracias a la máquina frigorífica
Por tanto, el flujo de calor que entra en la máquina frigorífica es
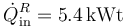
El coeficiente de desempeño de un refrigerador, por definición, es igual a
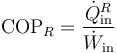
y por tanto, la potencia necesaria para hacer funcionar el refrigerador es

3 Flujo de calor
La potencia del apartado anterior es suministrada por un generador

siendo el rendimiento un 30%, por tanto,
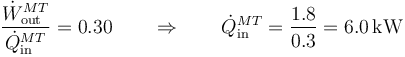
4 Consumo de combustible
El resultado anterior indica que se precisan 6 kJ/s de calor. A lo largo de un día se necesitarán
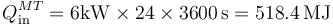
Si cada litro aporta 36MJ el consumo será