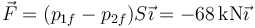Paso de calor entre dos cámaras rígidas
De Laplace
| (2 ediciones intermedias no se muestran.) | |||
| Línea 10: | Línea 10: | ||
==Temperatura final== | ==Temperatura final== | ||
| - | |||
| - | |||
Al ser el recipiente adiabático, todo el calor que sale de una de las cámaras entra en la otra | Al ser el recipiente adiabático, todo el calor que sale de una de las cámaras entra en la otra | ||
| Línea 20: | Línea 18: | ||
<center><math>n_1c_v(T_1-T_f)=n_2c_v(T_f-T_2)\qquad \Rightarrow\qquad T_f=\frac{n_1T_1+n_2T_2}{n_1+n_2}</math></center> | <center><math>n_1c_v(T_1-T_f)=n_2c_v(T_f-T_2)\qquad \Rightarrow\qquad T_f=\frac{n_1T_1+n_2T_2}{n_1+n_2}</math></center> | ||
| - | + | Calculamos el número de moles de cada gas | |
| - | <center><math>n_1 = \frac{pV}{RT_1}= \frac{pV}{ | + | <center><math>n_1 = \frac{pV}{RT_1}= 20.45\,\mathrm{mol}\qquad\qquad n_2 = \frac{pV}{RT_2}= 40.89\,\mathrm{mol}=2n_1</math></center> |
y por tanto, la temperatura final es | y por tanto, la temperatura final es | ||
| - | <center><math>T_f = \frac{ | + | <center><math>T_f = \frac{20.45\times 600+40.89\times 300}{20.45+40.89}=400\,\mathrm{K} |
</math></center> | </math></center> | ||
| Línea 32: | Línea 30: | ||
La cantidad de calor que pasa de una cámara a la otra es | La cantidad de calor que pasa de una cámara a la otra es | ||
| - | <center><math>Q_\mathrm{2in}=n_2c_v(T_f-T_2) | + | <center><math>Q_\mathrm{2in}=n_2c_v(T_f-T_2)\,</math></center> |
| - | + | La capacidad calorífica molar a volumen constante es, para el aire seco | |
| + | |||
| + | <center><math>c_v = \frac{R}{\gamma-1}=\frac{8.314}{0.4}\,\frac{\mathrm{J}}{\mathrm{K}\cdot\mathrm{mol}} = 20.79\,\frac{\mathrm{J}}{\mathrm{K}\cdot\mathrm{mol}}</math></center> | ||
| + | |||
| + | y por tanto el calor | ||
| + | |||
| + | <center><math>Q_\mathrm{2in}=20.45\times 20.79(400-300)\,\mathrm{J}=85\,\mathrm{kJ}</math></center> | ||
| + | |||
| + | ==Fuerza sobre la pared== | ||
| + | La fuerza se debe a la diferencia de presiones entre las dos cámaras. | ||
| + | La presión final de cada una cumple, por ser el volumen constante, | ||
<center><math>\frac{p_{nf}}{T_f}=\frac{p}{T_n}\qquad\Rightarrow\qquad p_{nf}=\frac{T_f}{T_n}p\qquad n = 1,2</math></center> | <center><math>\frac{p_{nf}}{T_f}=\frac{p}{T_n}\qquad\Rightarrow\qquad p_{nf}=\frac{T_f}{T_n}p\qquad n = 1,2</math></center> | ||
| Línea 41: | Línea 49: | ||
<center><math>p_{1f}=\frac{400}{600}102\,\mathrm{kPa}=68\,\mathrm{kPa}\qquad\qquad p_{2f}=\frac{400}{300}102\,\mathrm{kPa}=136\,\mathrm{kPa}</math></center> | <center><math>p_{1f}=\frac{400}{600}102\,\mathrm{kPa}=68\,\mathrm{kPa}\qquad\qquad p_{2f}=\frac{400}{300}102\,\mathrm{kPa}=136\,\mathrm{kPa}</math></center> | ||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
Puesto que conocemos la diferencia de presiones y el área de la pared (1m² por ser un cubo de 1m³ de volumen), la fuerza es inmediata | Puesto que conocemos la diferencia de presiones y el área de la pared (1m² por ser un cubo de 1m³ de volumen), la fuerza es inmediata | ||
<center><math>\vec{F}=(p_{1f}-p_{2f})S\vec{\imath}=-68\,\mathrm{kN}\vec{\imath}</math></center> | <center><math>\vec{F}=(p_{1f}-p_{2f})S\vec{\imath}=-68\,\mathrm{kN}\vec{\imath}</math></center> | ||
[[Categoría:Problemas del primer principio de la termodinámica (GIE)]] | [[Categoría:Problemas del primer principio de la termodinámica (GIE)]] | ||
última version al 08:52 11 jun 2016
Contenido |
1 Enunciado
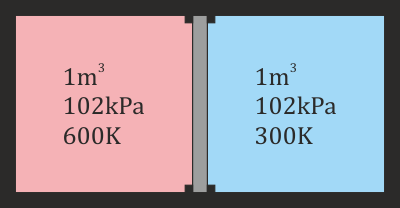
Un recipiente adiabático de 2 m³ está dividido en dos cámaras cúbicas del mismo tamaño, separadas por una pared inmóvil rellena de un aislante térmico. Las dos cámaras están llenas de aire seco. La de la izquierda contiene aire a 102 kPa y 600 K. El aire de la derecha está también a 102 kPa, pero a 300 K. Sin quitar la pared central se retira el aislante térmico que contiene, permitiendo que las dos cámaras entren en contacto térmico entre sí (no con el exterior)
- Determine la temperatura final de equilibrio y la cantidad de calor que pasa de una cámara a la otra.
- Halle la fuerza sobre la pared central una vez que se ha alcanzado el equilibrio térmico.
Datos Constante universal de los gases ideales: 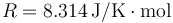 ; cociente entre capacidades caloríficas para el aire γ = 1.4.
; cociente entre capacidades caloríficas para el aire γ = 1.4.
2 Temperatura final
Al ser el recipiente adiabático, todo el calor que sale de una de las cámaras entra en la otra
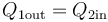
y, por ser los dos procesos a volumen constante y tratarse del mismo gas en ambas cámaras
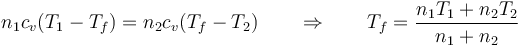
Calculamos el número de moles de cada gas
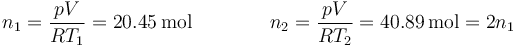
y por tanto, la temperatura final es
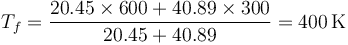
3 Calor transferido
La cantidad de calor que pasa de una cámara a la otra es
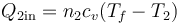
La capacidad calorífica molar a volumen constante es, para el aire seco
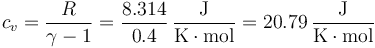
y por tanto el calor
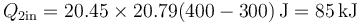
4 Fuerza sobre la pared
La fuerza se debe a la diferencia de presiones entre las dos cámaras. La presión final de cada una cumple, por ser el volumen constante,
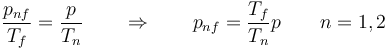
Esto nos da

Puesto que conocemos la diferencia de presiones y el área de la pared (1m² por ser un cubo de 1m³ de volumen), la fuerza es inmediata